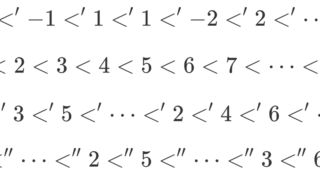順序数に関する基本的なこと

順序数とは，整列集合の構造を表すシンボルです。整列集合はどの2つの整列集合も必ず「大小比較」できるため，順序数自体も整列集合になります。

本記事では，整列集合の構造を表す「順序数」に関して，集合と位相の観点から基本的なことをまとめます。数学基礎論に深入りすることはなく，厳密性よりも感覚的な説明にとどめます。

本記事では， $\mathbb{N}=\{0,1,2,3,\ldots\}$ を， $0$ 以上の整数全体とします。今回は $\mathbb{N}$ に $0$ を含みます。

整列集合の分類
順序数を帰納的に定める
最小の非可算順序数に到達するまで無限に続く階段
最小の非可算順序数 ω1 へ
順序数に関する大事な性質
1. 可算集合では ω1 に到達できない
2. 後続順序数と極限順序数
関連する記事

整列集合の分類

順序数とは，整列集合の構造を表すシンボルです。整列集合とは，全順序集合かつ，空でない任意の部分集合が最小元をもつような集合を指します。詳しくは以下で解説しています。整列集合については既知とします。

整列集合 $X$ に対し， $a\in X$ より小さい元の集合 $X\langle a\rangle =\{ x\in X\mid x<a\}$ を $X$ の元 $a$ による切片 (section) といいます。上のリンク先に，次のような比較定理があります。

定理（整列集合の比較定理）

$X,Y$ を空でない整列集合とするとき，以下のいずれか一つのみが必ず成立する。

$X\simeq Y$

ある $a\in X$ が存在して， $X\langle a\rangle \simeq Y$

ある $b\in Y$ が存在して， $X\simeq Y\langle b\rangle$

ただし， $\simeq$ は順序同型であることを表す。

1.のとき $X$ と $Y$ を同一視(同値類による商集合と解釈)し，2.のとき $X>Y$ とし，3.のとき $X<Y$ と定めると，整列集合全体そのものも整列集合になると思えます。「思える」というのは感覚的な話で，実際には「整列集合全体の集合」なんて集合の公理に反するので考えることはできませんが，そういうイメージです。

整列集合全体の集合を，同型のものを同一視した商集合の各元を順序数 (ordinal number) ということにすると，全ての整列集合は，いずれかただ一つの順序数と同型だと考えられます。

順序数とは，このように整列集合の構造を表すシンボルと考えられます。

順序数を帰納的に定める

具体的に，順序数を帰納的に定めましょう。まず，

0 =\emptyset

と定義します。 $\emptyset$ は空集合です。それから，

1= \{0\} = \{\emptyset\}

と定めます。また， $0<1$ と整列順序を入れます。同様に，

2= \{ 0,1\} =\bigl\{\emptyset, \{\emptyset\}\bigr\}

とし， $0<1<2$ と整列順序を入れます。同様に，

3 = \{0,1,2\} = \Bigl\{\emptyset,\bigl\{\emptyset\}, \{\emptyset, \{\emptyset\}\bigr\}\Bigr\}

と定め， $0<1<2<3$ と整列順序を入れます。このように， $n$ まで定義された状態において， $n+1$ を

n+1= \{ 0,1,2,\ldots, n\}

と定義します。すなわち， $n+1$ は $n$ までの全てを含む集合と定義します。さらに $0<1<2<\cdots <n< n+1$ と整列順序を定めます。すなわち， $n+1$ 自体は整列集合であり，かつ $n+1$ 自体も $1,\ldots, n<n+1$ のように，これまでのどの元よりも大きい元とみます。 これにより，順序数 $i,j$ に対し， $i<j\iff i\in j\iff i\subsetneq j$ です。

このように，帰納的に定義された $0, 1,2,3\ldots, n,\ldots$ が順序数 (ordinal number) です。ここでいう帰納法とは，自然数全体しか到達できない数学的帰納法ではなく，超限帰納法とします。

定義した「整数」 $0,1,2,3,\ldots$ に対し，さらにそれを全て含む集合

\Large\color{red}\omega = \{0,1,2,3,\ldots \}

を定めることができます。 $\omega$ は，集合としては自然数全体の集合 $\mathbb{N}$ ですが，ここでは整列順序

0<1<2<3<\cdots< \omega

を考えます。 $\ldots$ の部分には，無限個の元がありますが，これは整列順序です。

さらに $0$ から $\omega$ までの整列集合を

\omega+1 = \{0,1,2,\ldots, \omega\}

とあらわします。わざわざ毎回 $\cdots$ をかくのも面倒なので， $\omega+1=[0,\omega]$ とかくことにしましょう。同様に， $\omega = [0, \omega)$ とかきましょう。今後もこのかき方を利用します。

定義から， $\omega$ は最小の可算順序数になります。すなわち， $\omega$ は可算集合で，かつ $n<\omega$ となる順序数 $n$ は全て有限集合です。

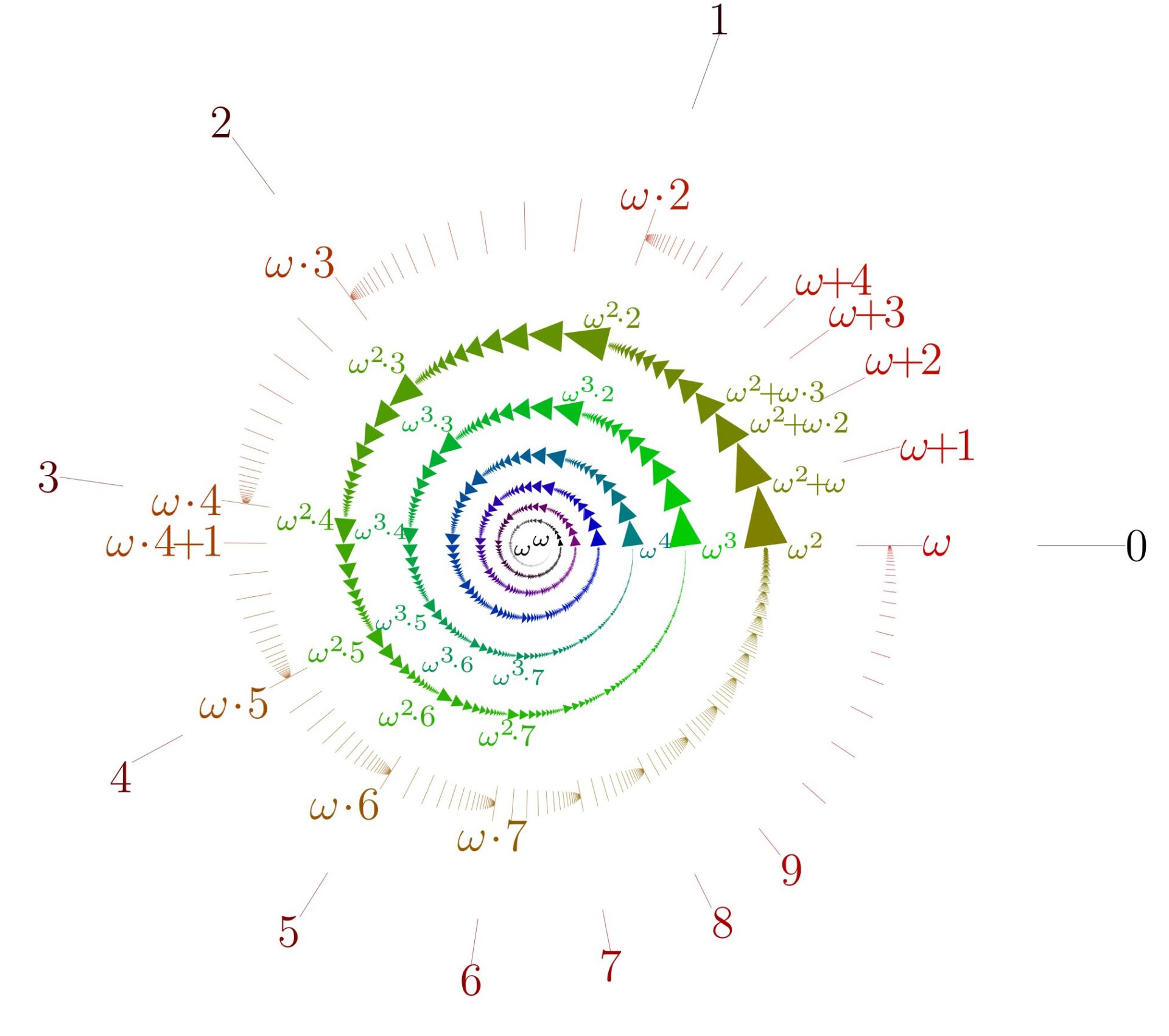
最小の非可算順序数に到達するまで無限に続く階段

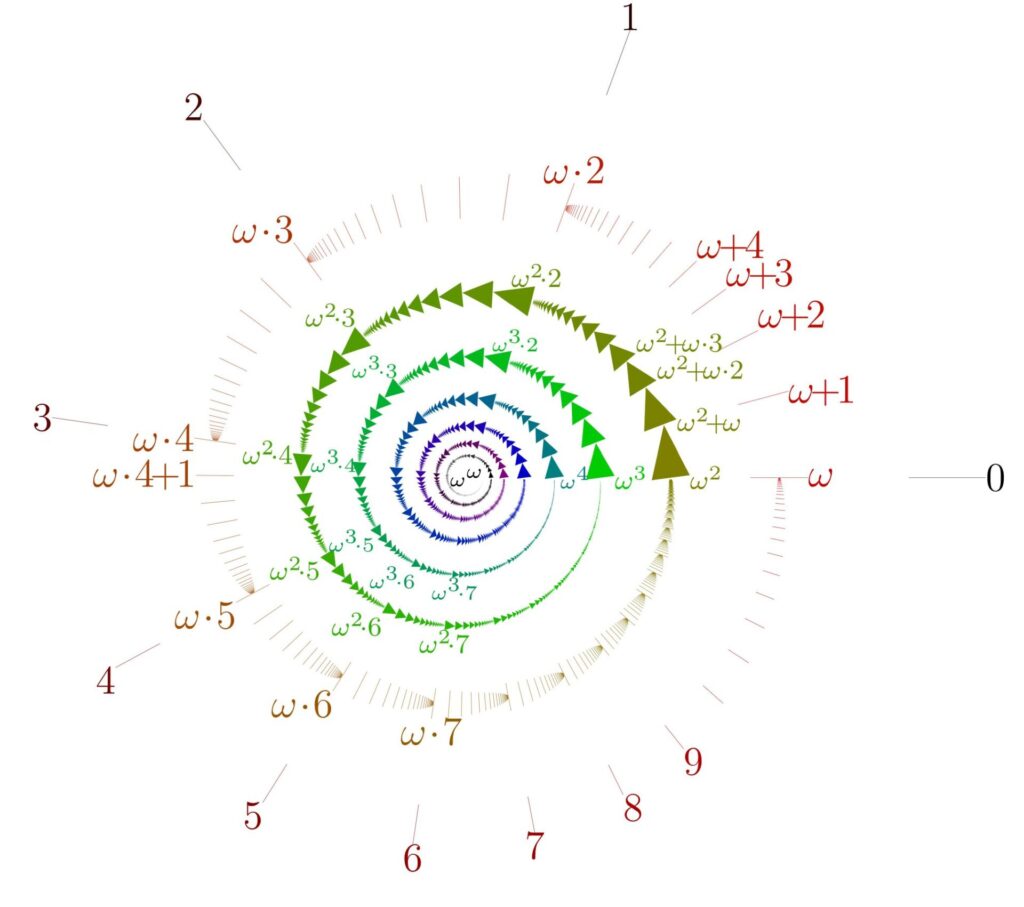
$\omega$ 以降も，以下のように順次に順序数が定義できます。

\omega+1,\: \omega+2, \:\ldots, \omega+n ,\ldots

$\omega+n$ は集合 $\mathbb{N}\cup \{ 0', 1',\ldots, (n-1)'\}$ に $0<1<\cdots< 0'<1'<\cdots<(n-1)'$ という整列順序を入れた集合に同型です。

$\omega+1,\: \omega+2,\ldots$ を可算無限回続けた極限として， $\omega +\omega$ も定義できます。これを， $\Large\color{red} \omega\cdot 2$ とかくことにしましょう。

ω・2 の構造

$\omega\cdot 2$ の構造は，集合 $\mathbb{N}\cup \{0', 1', 2',\ldots\}$ に

0<1<2<\cdots < 0'<1'<2'<\cdots

という整列順序をいれたものだと想像がつくでしょう。

ω・2の構造

$\omega\cdot 2$ は $\{0,1\}\times \mathbb{N}$ 上の元 $(a_1, a_0)$ に(左を優先する)辞書式順序をいれた整列集合 $(\{0,1\}\times \mathbb{N}, \le)$ に順序同型である。

辞書式順序というだけで，ふつうは左を優先します。すなわち，左から見ていきます。

$\omega\cdot 2$ のあと，さらに， $\omega\cdot 2+1, \:\omega\cdot 2+2,\ldots$ と続き，

\omega\cdot 2, \ldots, \omega \cdot 3, \ldots\hspace{0.5pt}\ldots, \omega \cdot n,\ldots

と続きます。 $\omega \cdot n$ は， $\{0,1,\ldots, n-1\}\times \mathbb{N}$ の元 $(a_1, a_0)$ に(左を優先する)辞書式順序をいれた整列集合と同型です。

$\omega\cdot 2,\omega\cdot 3,\omega\cdot 4, \ldots$ と可算無限回続けた極限として， $\omega\cdot\omega$ に到達できると予想できるでしょう。これを $\Large\color{red} \omega^2$ とかくことにします。

ω^2 の構造

$\omega^2$ の構造は想像がつくでしょう。

ω^2の構造

$\omega^2$ は $\mathbb{N}^2= \mathbb{N}\times \mathbb{N}$ 上の元 $(a_1, a_0)$ に(左を優先する)辞書式順序をいれた整列集合 $(\mathbb{N}^2, \le)$ に順序同型である。

また同様に， $\omega^2+1,\:\omega^2+2,\ldots$ と続き， $\omega^2+\omega$ や， $\omega^2\cdot 2, \omega^2\cdot 3$ とかも出てきますが，さらに進めると，

\omega^2 ,\ldots, \omega^3,\ldots\hspace{0.5pt}\ldots,\omega^n, \ldots

となります。 $\omega^n$ は， $\mathbb{N}^n$ 上の元 $(a_{n-1}, \ldots, a_1, a_0)$ に(左を優先する)辞書式順序をいれた整列集合と同型です。

さらに $\omega^2,\omega^3,\omega^4,\ldots$ を可算無限回続けると，極限として $\Large \color{red}\omega^\omega$ に到達します。

ω^ω の構造

ω^ωの構造

$\omega^\omega$ は，有限個の要素のみが $0$ でない左に無限に続く $(\ldots ,a_3, a_2,a_1, a_0)$ の集合 $\mathbb{N}^\mathbb{N}_0$ に(左を優先する)辞書式順序をいれた整列集合 $(\mathbb{N}^\mathbb{N}_0, \le)$ に順序同型である。

有限個の要素のみが $0$ でないというのはポイントです。実際，任意の順序数 $\alpha<\omega^\omega$ は，ある $n \ge 1$ が存在して， $\alpha<\omega^n$ になっているので， $\alpha$ を $(\ldots, a_3, a_2, a_1,a_0)$ の形と同一視したときには，「(各 $a_i$ を数字の桁のように見たときに) $n$ 桁」以下でなければなりません。一方，もし「有限個の要素のみが $0$ でない」を課していないと，たとえば $(\ldots, 1, 1, 1, 1)$ の上界に対応する $\omega^n$ が存在しません。

$\omega^\omega$ まで到達する様子をイメージにしたものが，最初にも取り上げた以下の図です。

イプシロン数 ε0

上の図は $\omega^\omega$ までしかありませんが，まだまだ永遠に続きます。 $\omega^\omega +1$ や $\omega^\omega+\omega$ などもそうですが，どんどん続けていくと，

\omega^{\omega^\omega} , \ldots, \omega^{\omega^{\omega^\omega}}, \ldots

と続き，さらに続けると，極限

\Large\color{red}\varepsilon_0= \omega^{\omega^{\cdot^{\cdot^{\cdot}}}}

に到達します。 $\varepsilon_0$ は， $\varepsilon^\omega =\varepsilon$ をみたす最小の $\varepsilon$ で，最小のイプシロン数 (epsilon number) といいます。

最小のイプシロン数というだけあって，さらに後ろに $\varepsilon_1=\varepsilon_0^{\varepsilon_0^{\cdot^{\cdot^{\cdot}}}},\ldots$ や， $\varepsilon_\omega , \ldots,\varepsilon_{\varepsilon_0},\ldots, \varepsilon_{\varepsilon_{\varepsilon_{\cdot_{\cdot_{\cdot}}}}}$ という風に，永遠に続きます。

終わりはないのです。

※注濃度との関係

ここまで取り上げた $\omega , \omega\cdot 2, \omega^2, \omega^\omega, \varepsilon_0, \varepsilon_{\varepsilon_{\varepsilon_{\cdot_{\cdot_{\cdot}}}}}$ はどの2つも順序同型ではありませんが，濃度は全て同じで，可算濃度です。

「順序の同型」は順序を保つ全単射がなければなりませんが，「濃度が等しい」は，全単射でさえあれば良いです。順序数は，濃度の分類より細かいわけです。

実際， $\omega^\omega$ は可算集合であることを示しましょう。 $\omega^\omega$ は，有限個の要素のみが $0$ でない左に無限に続く $(\ldots ,a_3, a_2,a_1, a_0)$ の集合に(左を優先する)辞書式順序をいれた整列集合に同型でした。

長さ $n$ 以下である $(\ldots, 0,0, a_{n-1}, \ldots, a_1, a_0)$ 全体の集合を $A_n$ とすると， $A_n$ は可算集合であり， $\omega^\omega =\bigcup_{n=0}^\infty A_n$ なので，やはり $\omega^\omega$ は可算集合ですね。

ただし，有限集合に関しては，順序数が $n$ であることと，濃度が $n$ となることは同じことです。

最小の非可算順序数 ω1 へ

これまで， $0,1, \ldots, \omega, \ldots, \omega\cdot 2 ,\ldots,\omega^2,\ldots, \omega^\omega ,\ldots, \varepsilon_0,\ldots$ とさまざまな順序数を考えましたが，これらは集合とみると全て可算集合なのでした。この可算集合の階段は無限に続きます。では，非可算順序数は存在しないのかというとそういうわけではありません。それは，次の定理から分かります。

定理（整列可能定理）

任意の集合は，その上にある順序を定義して整列集合にすることができる。ただし，選択公理は認める。

この定理については，整列集合と整列可能定理で解説しています。実数全体の集合 $\R$ にも，通常の順序は整列順序ではありませんが，本定理より，ある整列順序を入れることが可能です。

$\R$ は非可算集合ですから， $\R$ を整列順序に並べたとき，ある非可算順序数と同型なはずです。したがって，非可算順序数の存在が言えました。

さて，最小の非可算順序数を $\Large\color{red} \omega_1$ としましょう。「最小」なので， $\alpha <\omega_1$ ならば， $\alpha$ は高々可算な順序数です。したがって， $\omega_1=[0,\omega_1)$ は，高々可算な順序数をすべて集めた集合ということができます。また，高々可算な順序数をすべて集めた集合は非可算集合になることがわかります。

他，濃度が上がっていく度に，その濃度における最小の順序数 $\omega_2, \omega_3,\omega_4,\ldots$ が定義されます。

順序数に関する大事な性質

大事な性質を一つ紹介しましょう。

可算集合では ω1 に到達できない

(可算)点列で， $\omega_1$ に収束するものは存在しないという定理です。

定理（可算集合では $\omega_1$ に到達できない）

$A\subset [0,\omega_1)$ が可算集合のとき， $\sup A<\omega_1$ である。

これにより，任意の点列 $\{x_n\}\subset [0,\omega_1)$ は $\omega_1$ に収束し得ないことがわかる。

$\sup A =\min \{ \zeta\mid \forall a\in A, \, a\le \zeta\}$ です。整列集合なので，これは存在します。

証明

任意の $\alpha\in A$ に対し， $[0,\alpha]$ は可算集合である。 $A$ は可算なので，

B=\bigcup_{\alpha\in A} [0,\alpha]

も可算集合である。 $\gamma =\min [0,\omega_1)\setminus B$ とおくと， $\beta\in B\iff \beta< \gamma$ である。 $\beta<\gamma$ となる $\beta$ が可算個なので， $\gamma<\omega_1$ である。

ゆえに， $\sup A<\omega_1$ である。

証明終

後続順序数と極限順序数

$0$ 以外の順序数は2つに分類できます。紹介しておきましょう。

定義（後続順序数と極限順序数）

順序数 $\alpha$ に対し，ある $\beta$ が存在して，

\alpha =\beta+1 =[0,\beta]

とかけるとき， $\alpha$ を後続順序数 (successor ordinal) という。

$0$ でも後続順序数でもない順序数を極限順序数 (limit ordinal) という。

たとえば， $5$ は $5=4+1=\{0,1,2,3,4\}$ なので，後続順序数です。一方で， $\omega$ は， $\omega =\beta+1$ となる順序数 $\beta$ は存在しないので，極限順序数です。