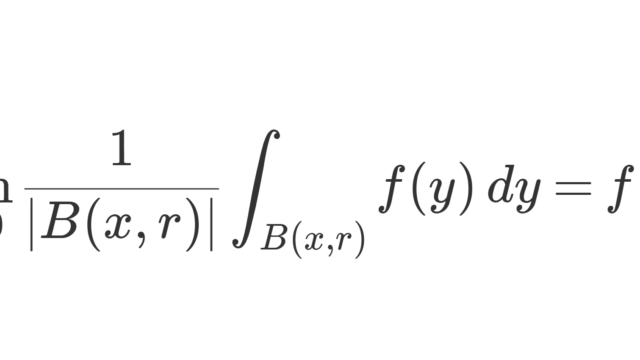 測度論
測度論 ルベーグの微分定理とその証明~測度の微分を添えて~
ルベーグの微分定理(Lebesgue differentiation theorem)は,リーマン積分のときに成り立っていた「積分して微分すると元に戻る」という性質の,ルベーグ積分版といえます。ルベーグの微分定理とその証明を行い,測度の微分について少し掘り下げましょう。
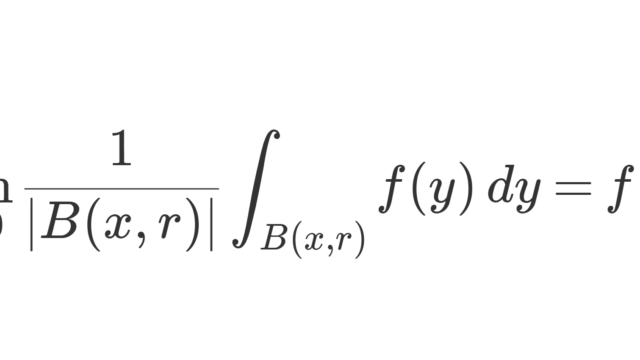 測度論
測度論  測度論
測度論  測度論
測度論  測度論
測度論  関数解析学
関数解析学  関数解析学
関数解析学  関数解析学
関数解析学 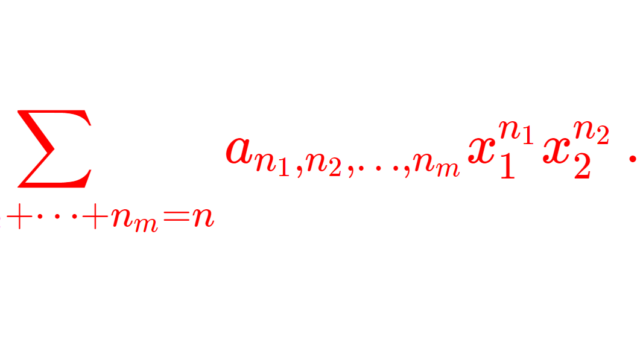 群・環・体
群・環・体 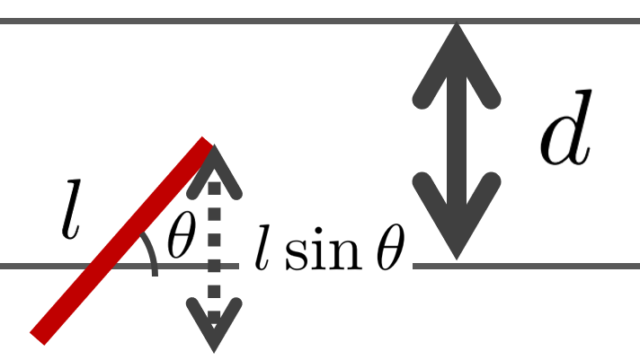 確率論
確率論 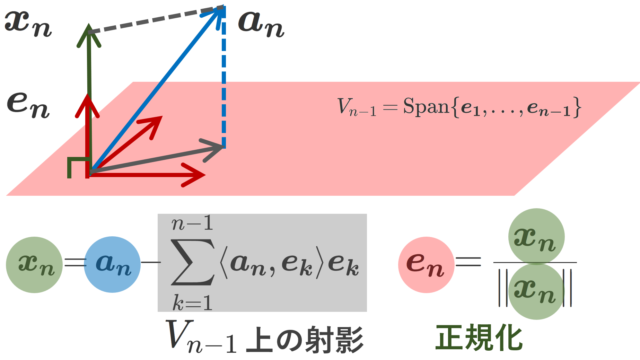 関数解析学
関数解析学