 線形代数学
線形代数学 数ベクトルの定義と数ベクトルにおけるノルム・内積
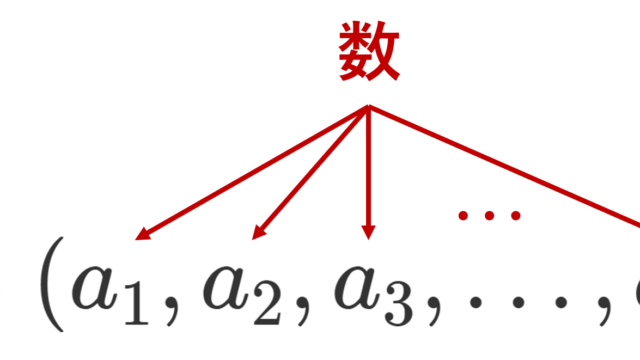
数ベクトルとは,ざっくりいうと数を並べたものです。数を並べたものを「ベクトル」という一つのかたまりとして扱うことで,いろいろ便利なことがあるわけです。今回は,「便利なこと」の紹介はしませんが,数ベクトルとは何かの定義とノルム・内積といった大切な概念を一気に解説しましょう。
 線形代数学
線形代数学  線形代数学
線形代数学  線形代数学
線形代数学  線形代数学
線形代数学 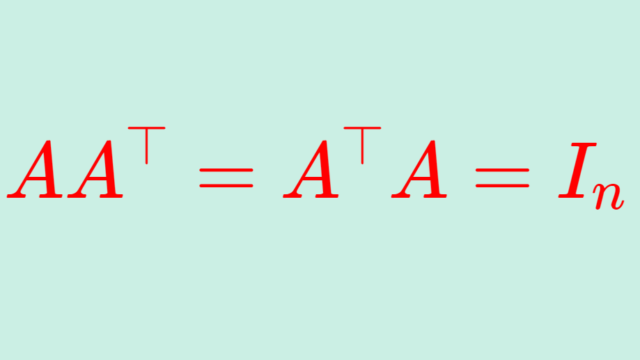 線形代数学
線形代数学  LaTeX
LaTeX 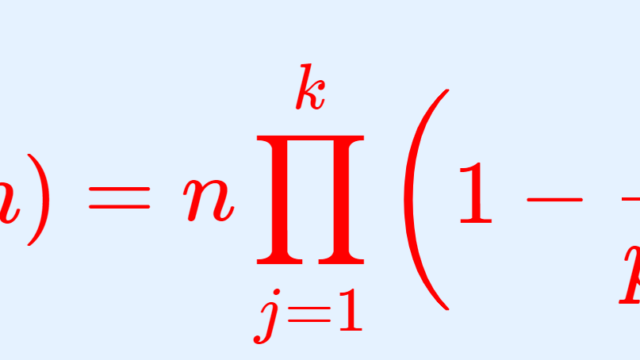 数論
数論 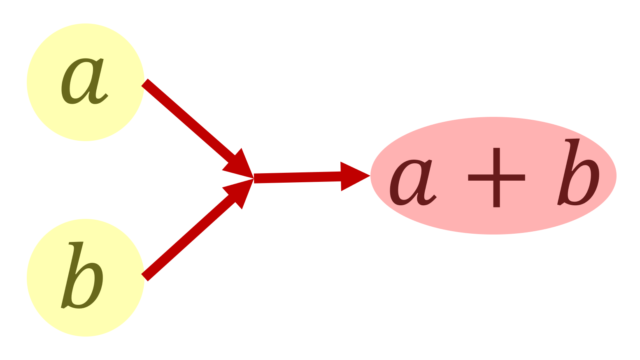 記号・記法
記号・記法  解析学(大学)その他
解析学(大学)その他 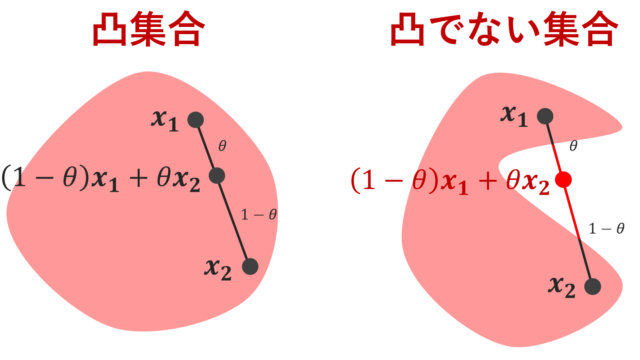 解析学(大学)その他
解析学(大学)その他