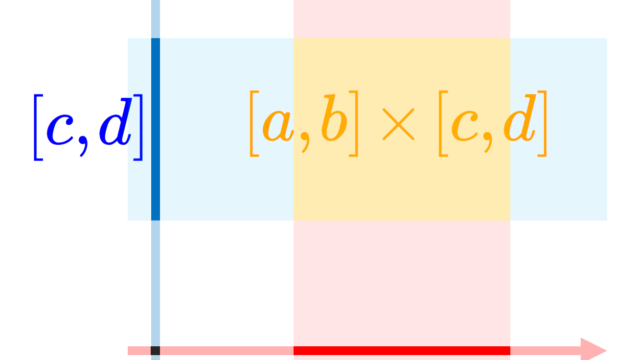 集合と位相
集合と位相 【直積集合】集合の直積について詳しく~具体例10個~
集合A,Bに対し,その直積 (direct product) A×Bは,a∈A, b∈Bの対(順序対)(a,b)の集合となります。そんな直積について,2個の直積・n個の直積・無限個の直積を,具体例を添えながら,順番に解説していきましょう。
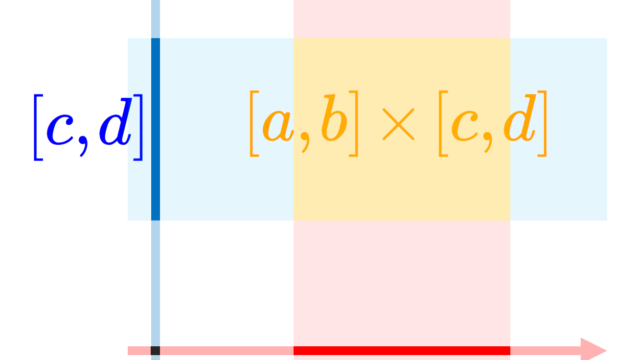 集合と位相
集合と位相  LaTeX
LaTeX 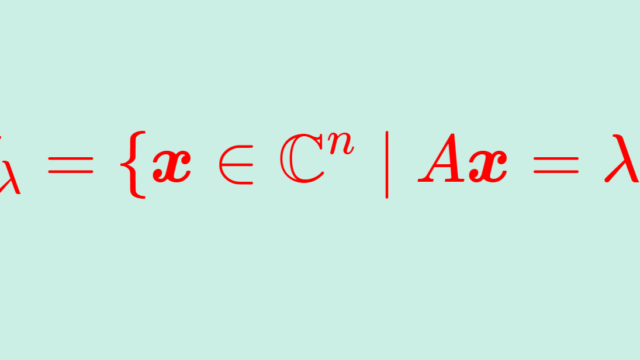 線形代数学
線形代数学  微分積分学(大学)
微分積分学(大学) 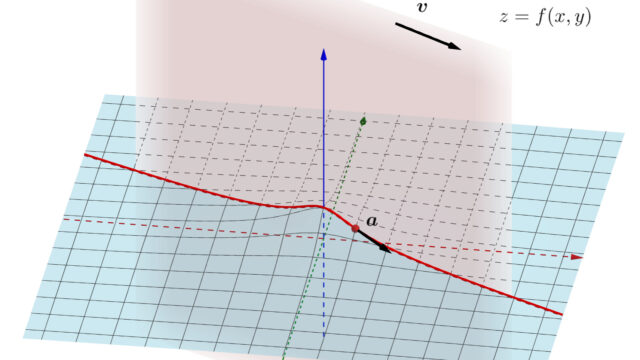 微分積分学(大学)
微分積分学(大学) 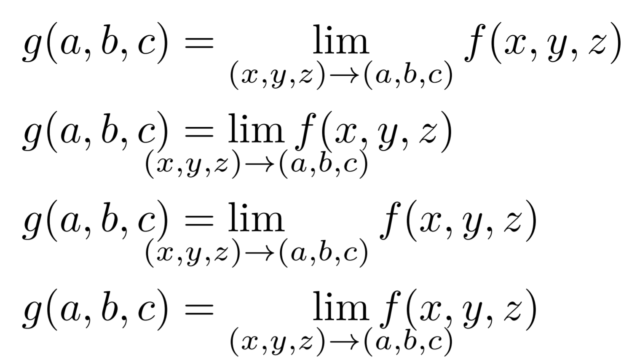 LaTeX
LaTeX 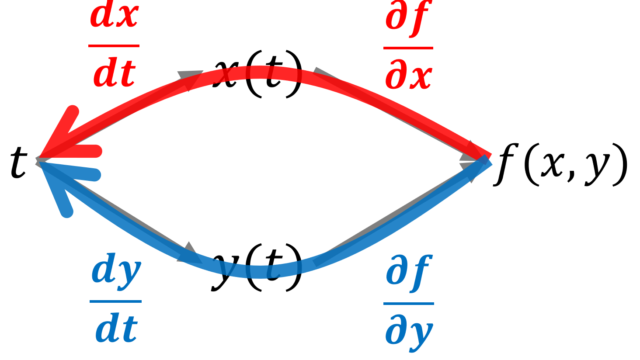 微分積分学(大学)
微分積分学(大学) 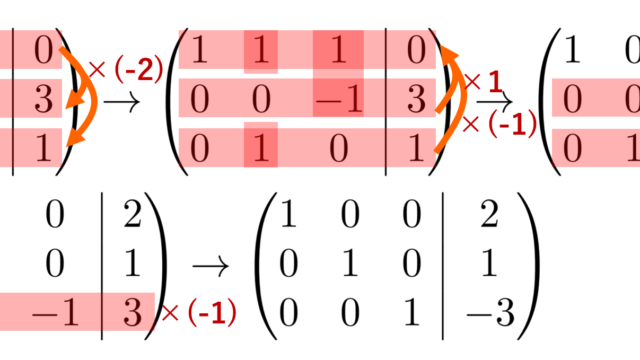 線形代数学
線形代数学 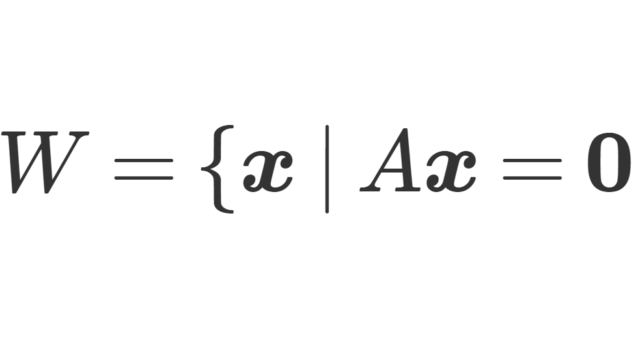 線形代数学
線形代数学 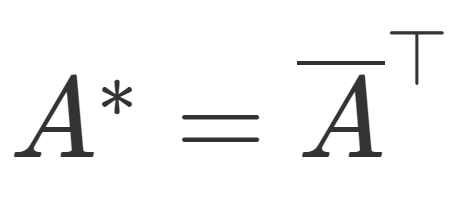 線形代数学
線形代数学