 LaTeX
LaTeX 【LaTeX】行間を変える方法【部分・全体】
LaTeXにおいて,部分的に行間を変える方法と,全体の行間を変える方法を,それぞれ解説します。
 LaTeX
LaTeX  LaTeX
LaTeX 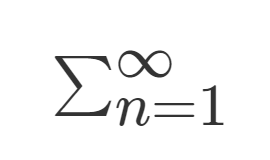 LaTeX
LaTeX  LaTeX
LaTeX  LaTeX
LaTeX 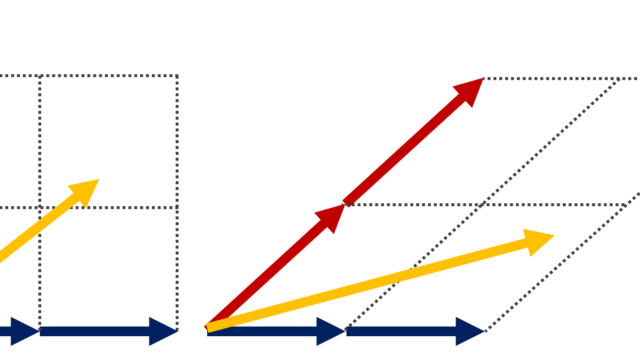 線形代数学
線形代数学 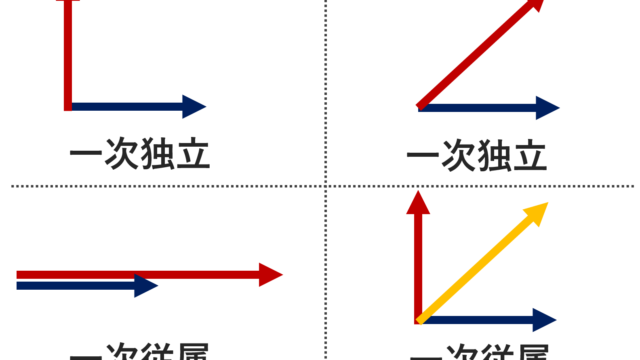 線形代数学
線形代数学 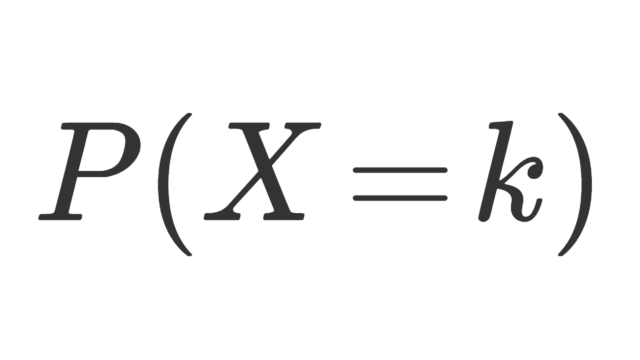 確率論
確率論 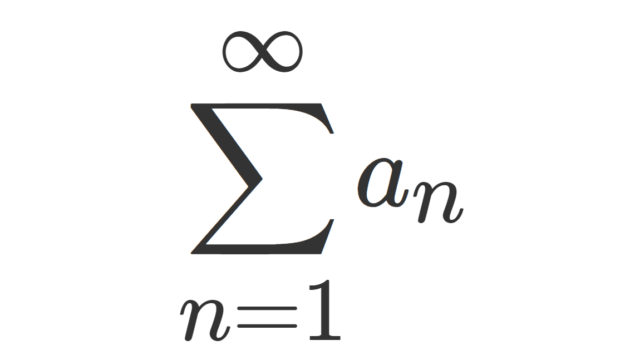 微分積分学(大学)
微分積分学(大学) 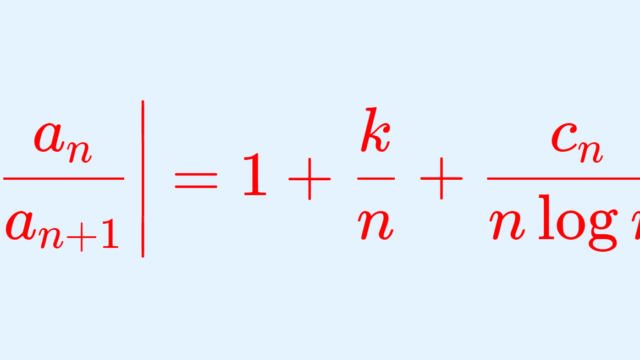 微分積分学(大学)
微分積分学(大学)