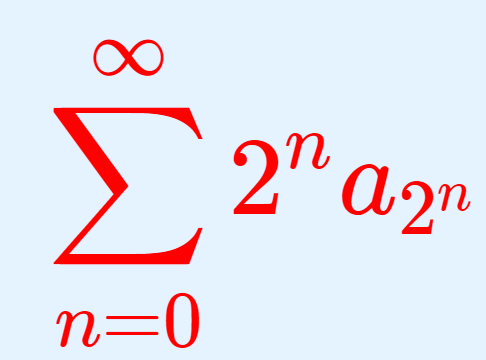 微分積分学(大学)
微分積分学(大学) 【級数の収束判定法】Cauchy Condensation Test
級数の収束判定法の1つである,Cauchy condensation test(あるいは日本語で「コーシーの凝集判定法」)について,その定理の主張と証明を追っていきましょう。
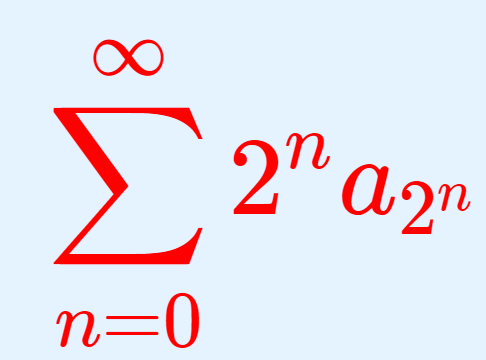 微分積分学(大学)
微分積分学(大学) 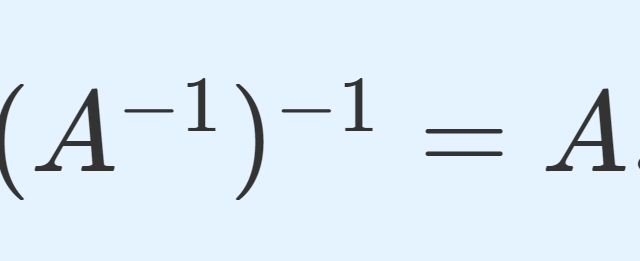 線形代数学
線形代数学  線形代数学
線形代数学  統計学
統計学 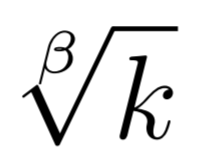 LaTeX
LaTeX 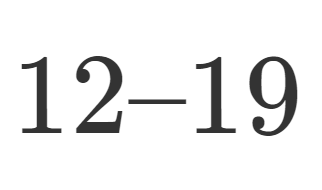 LaTeX
LaTeX  統計学
統計学 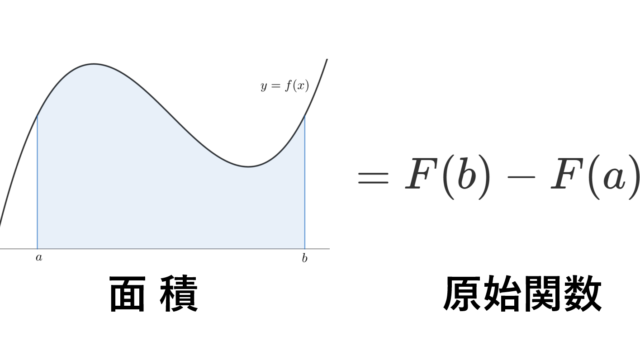 微分積分学(大学)
微分積分学(大学)  解析学(大学)その他
解析学(大学)その他  線形代数学
線形代数学