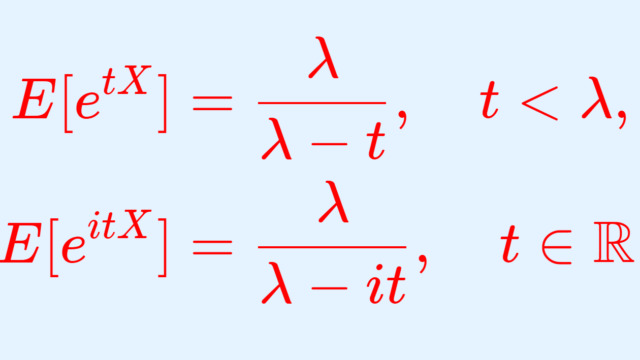 確率論
確率論 指数分布の積率母関数・特性関数とその導出証明
指数分布について,それの積率母関数(モーメント母関数)・特性関数について紹介し,それらの導出の証明を行いましょう
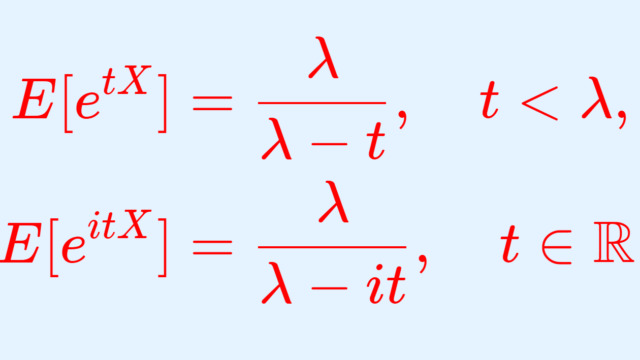 確率論
確率論 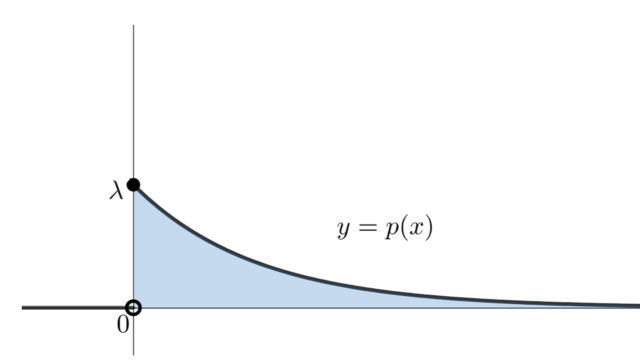 確率論
確率論  確率論
確率論  確率論
確率論  LaTeX
LaTeX  確率論
確率論  LaTeX
LaTeX  微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  LaTeX
LaTeX