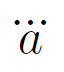 LaTeX
LaTeX 【LaTeX】アクセント記号のコマンド22個+16個一覧
LaTeXにおける,数式モード・文書モードそれぞれの,アクセント記号に関するコマンド22個・16個をまとめます。なお,一部 amsmath, amssymb, amsfonts の使用を仮定しているものがあります。うまくいかない場合は読み込んでみてください。
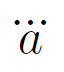 LaTeX
LaTeX 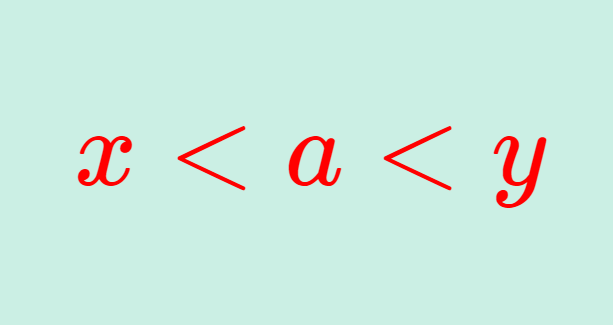 微分積分学(大学)
微分積分学(大学) 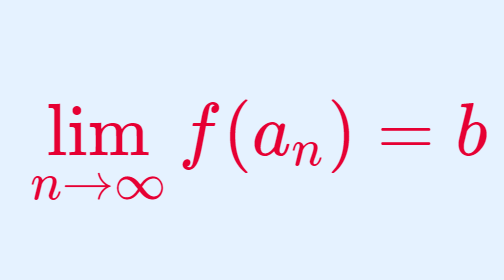 微分積分学(大学)
微分積分学(大学) 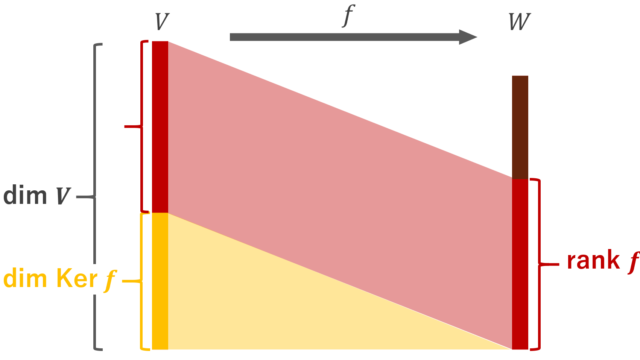 線形代数学
線形代数学 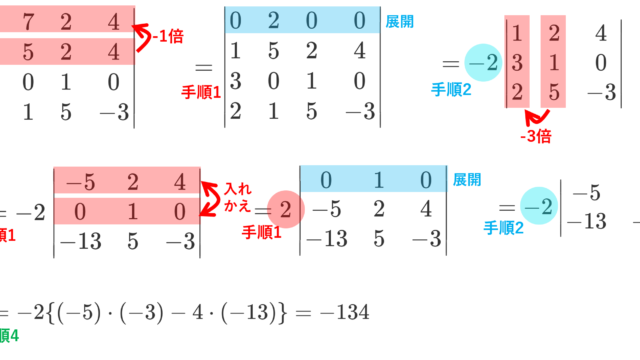 線形代数学
線形代数学 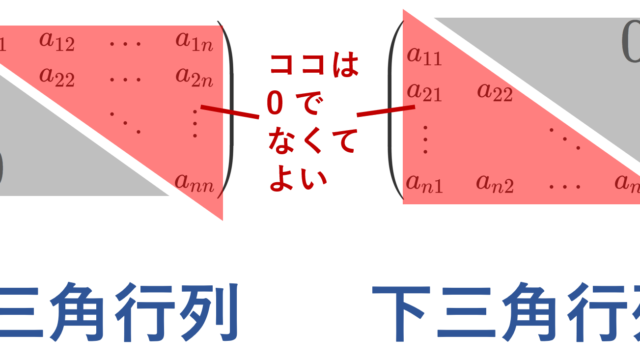 線形代数学
線形代数学  線形代数学
線形代数学 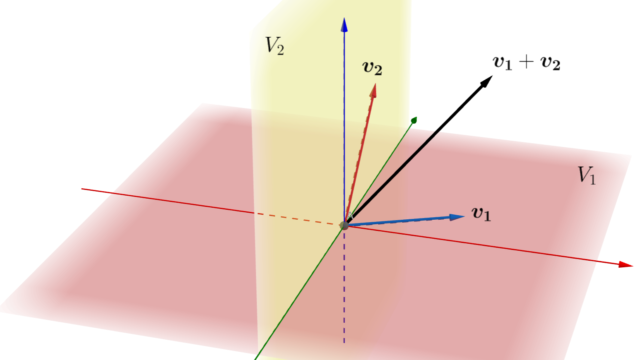 線形代数学
線形代数学  LaTeX
LaTeX 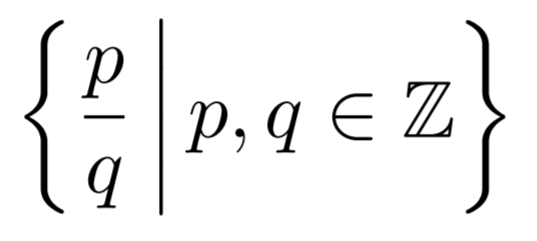 LaTeX
LaTeX