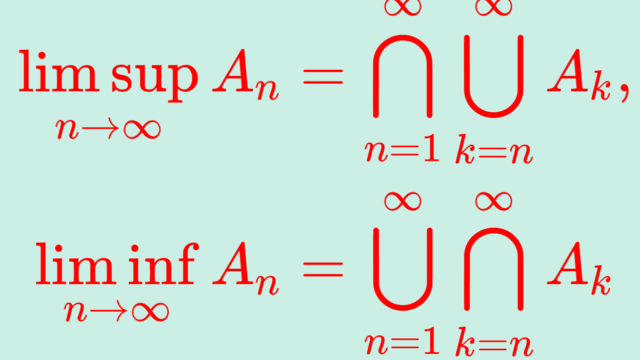 集合と位相
集合と位相 上極限集合・下極限集合の定義とその包含関係の証明
無限個の集合に対して定義される2つの極限集合(上極限集合・下極限集合)について,その定義と,日本語に直したときの意味と,包含関係の証明をします。他にも,極限集合が存在する十分条件や,数列と集合列の極限の比較も行います。
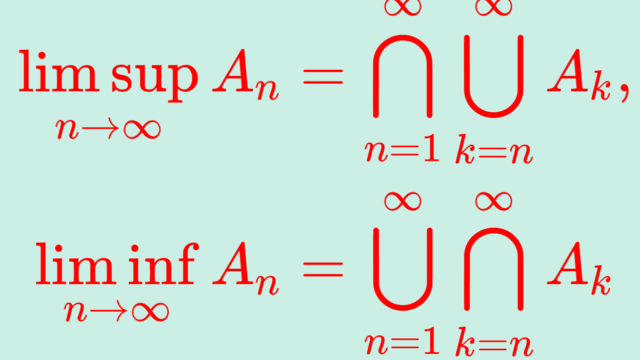 集合と位相
集合と位相  LaTeX
LaTeX  LaTeX
LaTeX  線形代数学
線形代数学 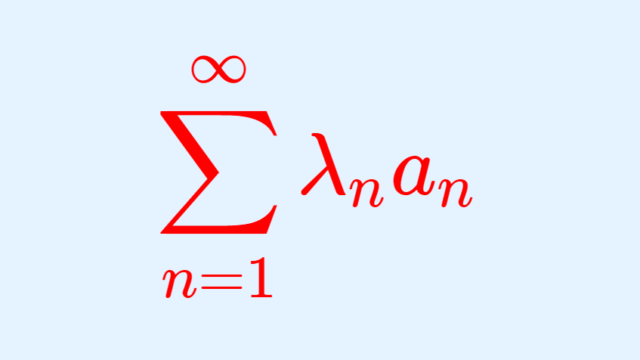 微分積分学(大学)
微分積分学(大学)  LaTeX
LaTeX 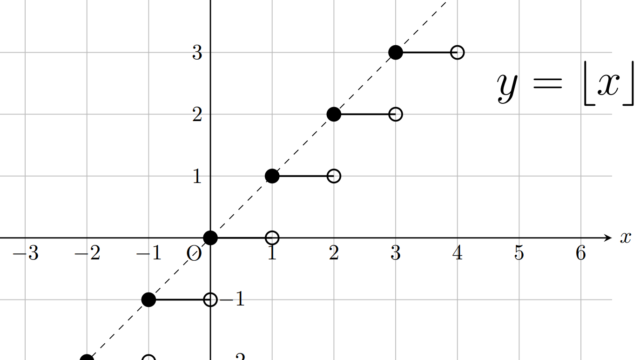 記号・記法
記号・記法 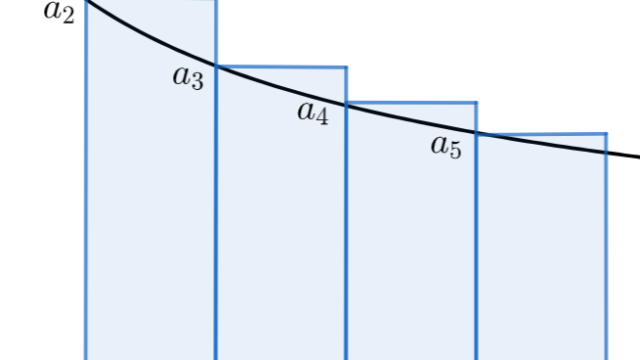 微分積分学(大学)
微分積分学(大学) 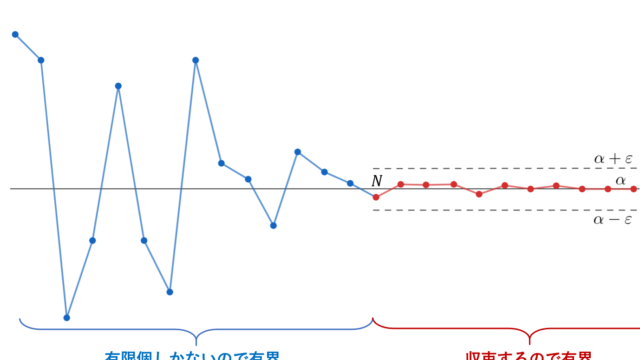 微分積分学(大学)
微分積分学(大学) 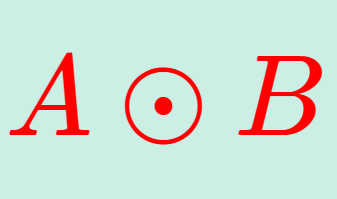 線形代数学
線形代数学