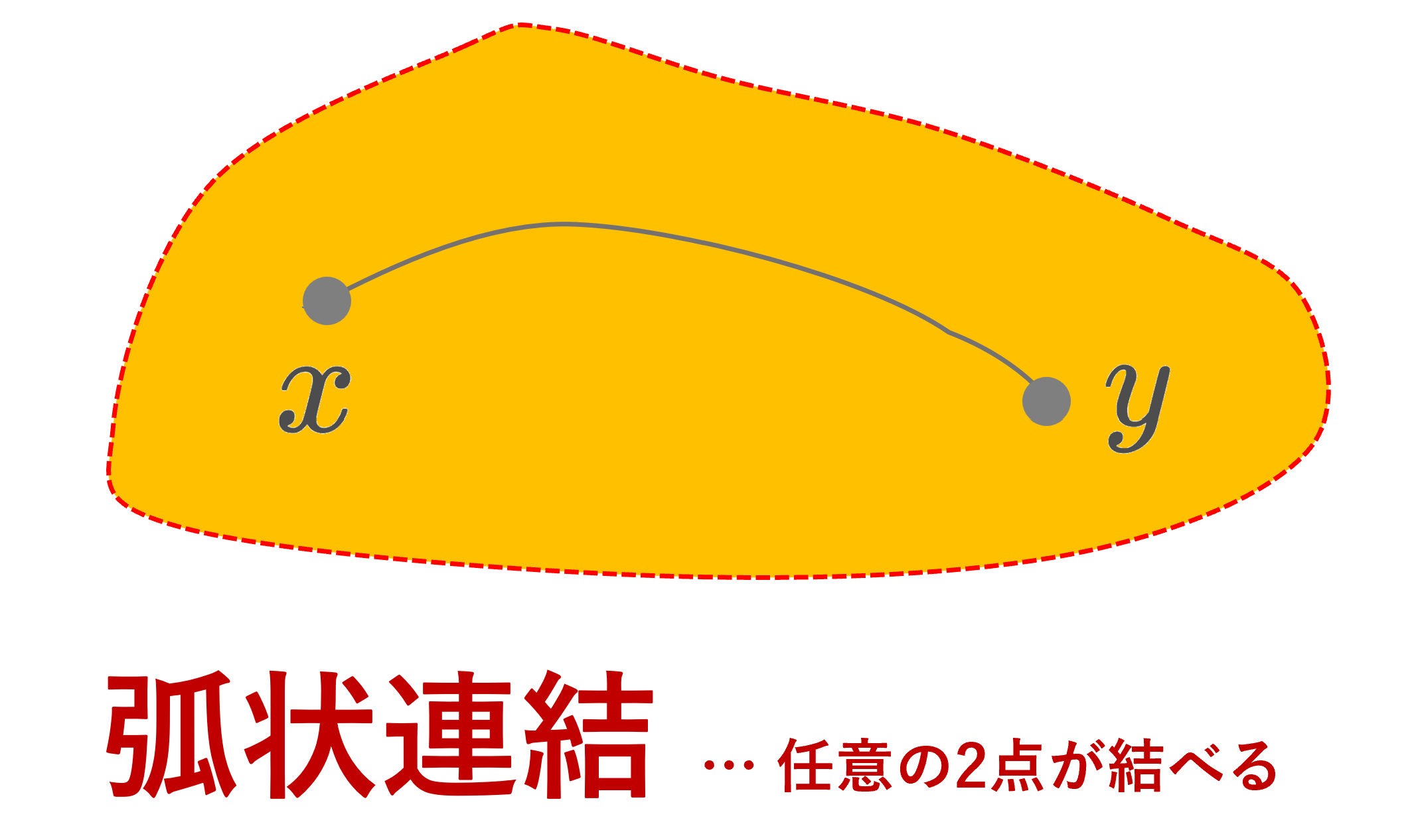
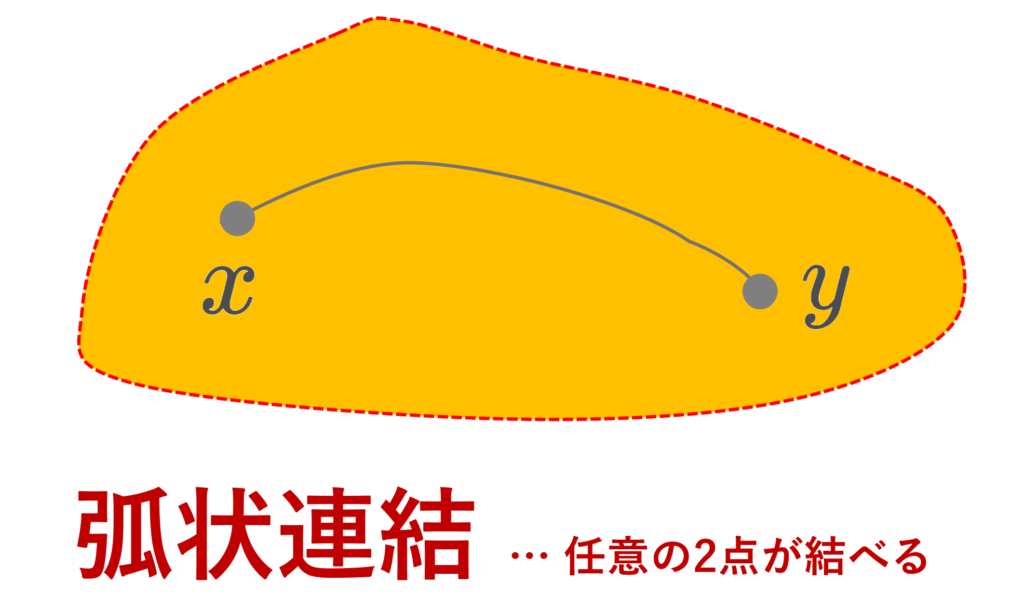
弧状連結とは,空間内の任意の2点が道で結べる,すなわち,単位区間からの連続写像が構成できるような位相空間のことをいいます。また,弧連結とは,道として弧が取れる,連続写像よりさらに強い同相写像が取れるような位相空間のことをいいます。
さらに局所弧状連結・局所弧連結についても述べましょう。
弧状連結・弧連結
弧状連結・弧連結と,関連して局所弧状連結・局所弧連結についても一気に定義しましょう。
弧状連結・弧連結の定義
定義1(弧状連結・弧連結)
(X,\mathcal{O}) を位相空間とし,A\subset X とする。
任意の異なる2点 x,y\in A に対して, f(0)=x,\, f(1)=y となる連続写像 f\colon [0,1]\to A が取れるとき, A は弧状連結 (path connected, pathwise connected) であるという。このときの f を x から y への道 (path) という。
さらに,この f として埋め込み,すなわち f\colon [0,1]\to f([0,1])\subset A が同相写像であるように取れるとき, A は弧連結 (arc connected, arcwise connected) であるという。このときの f を x から y への弧 (arc) という。
定義より明らかに弧連結 \implies 弧状連結です。 X がハウスドルフ空間 ( T_2 空間) であるときは,弧状連結であることと弧連結であることは同値になります。本記事では証明しません。
弧連結は,単に弧状連結の f\colon [0,1]\to X として全単射なものが取れるとき,と定義することもあります。文献[1]はそうです。文献による定義の違いに注意してください。
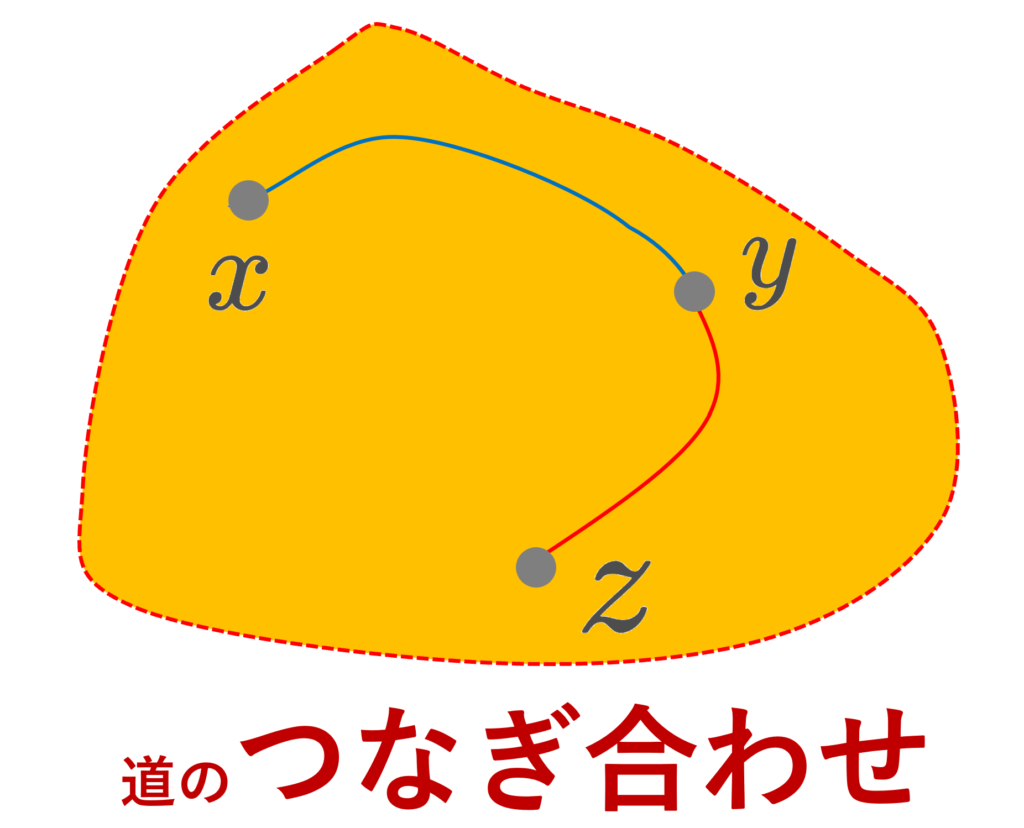
x から y への道 f_1 があって, y から z への道 f_2 がある場合は,x から z への道 f を,
f(t)=\begin{cases} f_1(2t) & 0\le t\le 1/2, \\f_2(2t-1) & 1/2\le t\le 1\end{cases}
とすることで構成可能です。これを本記事では,道のつなぎ合わせ (join) ということにします。
局所弧状連結・局所弧連結
局所性の定義もしておきましょう。
定義2(局所弧状連結・局所弧連結)
(X,\mathcal{O}) を位相空間とする。
任意の x\in X が,弧状連結な集合からなる基本近傍系を持つとき, X は局所弧状連結 (locally pathwise connected) であるといい,弧連結な集合からなる基本近傍系を持つとき, X は局所弧連結 (locally arcwise connected) という。
弧状連結だからといって局所弧状連結とは限らないし,逆に局所弧状連結だからといって弧状連結とは限りません。下の例で確認しましょう。
弧状連結・弧連結の具体例
連結との違いも含めて,具体例を述べましょう。
例1(1点集合).
1点集合 \{x\} は連結・弧状連結だが,弧連結ではない。
[0,1] と \{x\} とは全単射を構成できないので,弧連結にはなりませんね。
X を終域とする写像はどんな写像でも弧状連結ですが,その像は密着空間なので, [0,1] とは同相になりません。よって,弧連結にはなりません。
例3( \R とその部分集合).
\R や [0,1) などは連結・弧状連結・弧連結・局所連結・局所弧状連結・局所弧連結である。
[0,1)\cup [2,\infty) は連結・弧状連結・弧連結のいずれでもないが,局所連結・局所弧状連結・局所弧連結ではある。
後半が面白いです。全体としては穴が開いて連結ではないですが,各点の十分近くでは,局所的に連結・弧状連結・弧連結です。
異なる2点 x,y\in \R^2\setminus A を取りましょう。 x を通る \R^2 上の直線は非可算無限個あるので, A と共通部分をもたない直線も非可算無限個あります。同様に,y を通る直線のうち, A と共通部分をもたない直線も非可算無限個あります。
ゆえに, x を通る直線と y を通る直線のうち,交点をもつものを1つ取ってくることができます。ゆえに,x と y を弧で結ぶことが可能です。
例5(位相幾何学者の正弦曲線).
\R^2 の部分集合
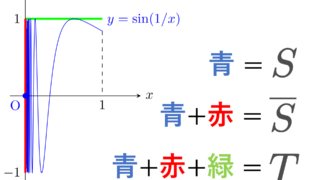
S=\left\{\left(x, \sin\frac{1}{x}\right)\middle| 0<x\le 1\right\}\cup \{(0,0)\}
とすると,その閉包は \overline{S} = S\cup \left(\{0\}\times [-1,1]\right) となる。
さらに, T=\overline{S}\cup \left([0,1]\times \{1\}\right) とする。
このとき, T は連結・弧状連結・弧連結である。S, \overline{S} は連結だが,弧状連結・弧連結ではない。
また, S,\overline{S}, T はどれも局所連結・局所弧状連結・局所弧連結ではない。
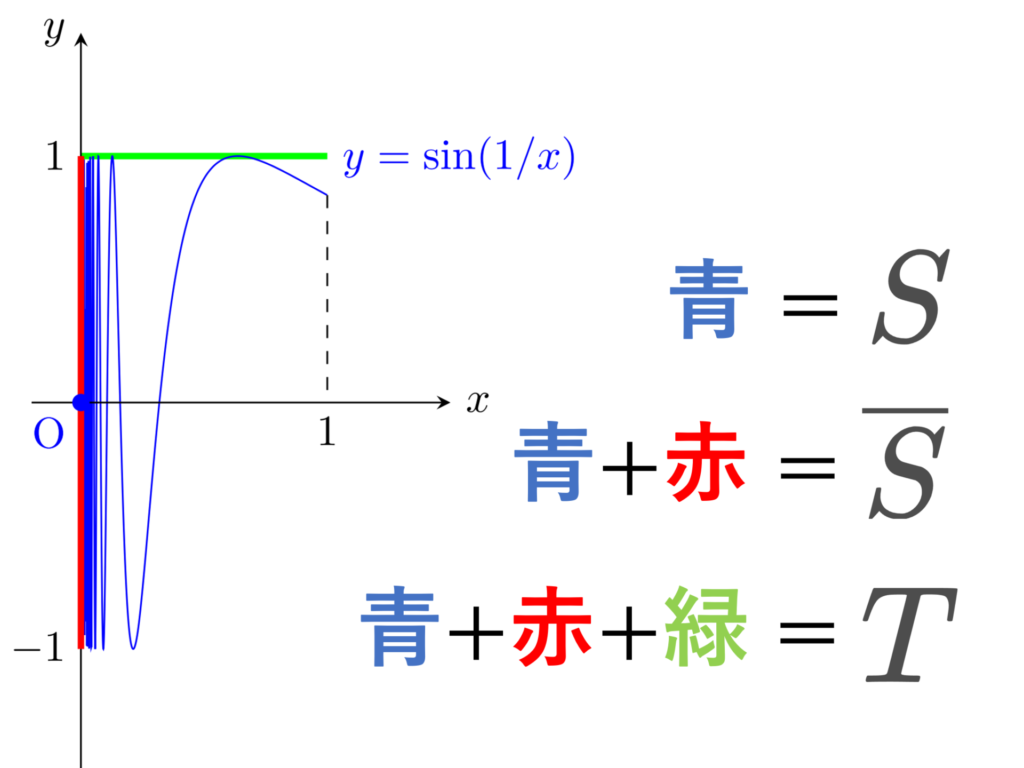
これは,連結だが弧状連結でない典型例です。後の定理1で弧状連結 \implies 連結を証明しますが,その逆は成立しません。なおこの例から,連結な集合の閉包は連結であることが知られていますが,弧状連結はそうでないこともわかります。
この空間の解説は,以下の記事で行っています。
類例として,くし空間 (comb space) というのもあります。【位相空間】くし空間(Comb Space)で解説しています。
例6(長い直線).
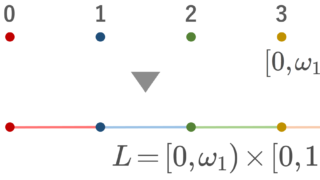
\omega_1 を最小の非可算順序数とする。このとき,長い直線 L = [0,\omega_1) と拡張された長い直線 L^*=[0,\omega_1] を考えると,
連結だが,長すぎて弧状連結にはできない例です。 [0,1] や数直線 \R よりはるかに長いので,連続写像 f\colon [0,1]\to L^* で,たとえば f(0)=0, f(1)=\omega_1 となるものは構成できないのです。詳しくは以下の記事で解説しています。
例7(補有限位相・補可算位相).
X を非可算集合とし,
\begin{aligned}\mathcal{O}_f&=\{\emptyset\}\cup \{ O\subset X\mid X\setminus O \text{ is finite}\} \\ \mathcal{O}_c&=\{\emptyset \}\cup \left\{O\subset X\middle|\begin{gathered} X\setminus O \text{ is at most} \\ \text{countable}\end{gathered}\right\} \end{aligned}
とする。このとき, (X,\mathcal{O}_f) を補有限位相, (X,\mathcal{O}_c) を補可算位相という。
(X,\mathcal{O}_f) は連結・局所連結であり,さらに連続体仮説を認めると弧状連結である。一方で (X,\mathcal{O}_c) は連結・局所連結だが,弧状連結ではない。
以下で解説しています。
弧状連結・弧連結の性質
性質を紹介し,証明しましょう。
1. 弧状連結ならば連結
例5.や例6.で挙げた通り,逆は成立しません。同様に, X が局所弧状連結ならば,局所連結です。
証明
x,y\in X とする。 X は弧状連結なので,ある連続写像 f\colon [0,1]\to X で, f(0)=x, \, f(1)=y となるものが存在する。
位相空間における連結性について詳しくで解説している通り, [0,1] は連結であり,かつ連結集合の連続像は連結なので, f([0,1]) も連結である。 x,y\in f([0,1]) であり, x,y を含む連結集合を取ってこれたから, X は連結である。
証明終
2. 弧状連結と連続写像
定理2(弧状連結と連続写像)
証明
1.について
y_1, y_2\in f(X) とすると,ある x_1, x_2\in X があって, f(x_1)=y_1, f(x_2)=y_2 とできる。
X は弧状連結なので, x_1 から x_2 への道 u\colon [0,1]\to X が存在するが,このときの f \circ u \colon [0,1]\to f(X) は y_1 から y_2 への道である。よって, f(X) は弧状連結である。
2.について
たとえば, Y が1点集合のときは, [0,1] から Y への全単射が存在しえないので,弧連結になることはない。
証明終
3. 連結+局所弧状連結 ⇒ 弧状連結
定理1も踏まえて言い換えれば,局所弧状連結な空間では,連結 \iff 弧状連結ということです。
証明
a\in X を一つ取り, H= \{ x\in X\mid \exists \text{path from } a \text{ to } x\},すなわち, a から x までの道が存在する x 全体の集合と定める。明らかに a\in H である。
H=X であることを示せば,X は弧状連結となって証明が終わるが, X は連結であるので,単に H が開かつ閉が示せれば十分である。
H が開であることを示そう。 x\in H とすると, a と x には道が存在する。
X は局所弧状連結なので,ある近傍 x \in U\subset X があって,x と U 上の任意の点は道で結べる。よって,道のつなぎ合わせによって, a と U 上の任意の点は道で結べる。ゆえに, U\subset H となるから, H は開集合である。
H が閉であることを示そう。 x\in \overline{H} とすると, X は局所弧状連結なので,ある近傍 x \in U\subset X があって,x と U 上の任意の点は道で結べる。
U\cap H\ne \emptyset より, b\in U\cap H を取ると, b と x は道で結べ, a と b も道で結べるので,道のつなぎ合わせによって,結局 x\in H である。ゆえに, H は閉集合である。
以上から, H が開かつ閉なので, H=X となるから,X は弧状連結である。
証明終
定理3から,次の系が導けます。
任意の x\in U に対して,ある \varepsilon >0 が存在して,任意の 0<\varepsilon'<\varepsilon に対し, \varepsilon'-近傍 \subset U とできるので, U は局所弧状連結といえます。よって先ほどの定理が使えるわけです。
U が開集合であることがポイントで,たとえば,例5.における \overline{S} は \R^2 における閉集合で,連結だが弧状連結ではありません。
なお, \R の場合は,開集合でなくても,連結であることと弧状連結であることは同値で,それは区間に限ります。
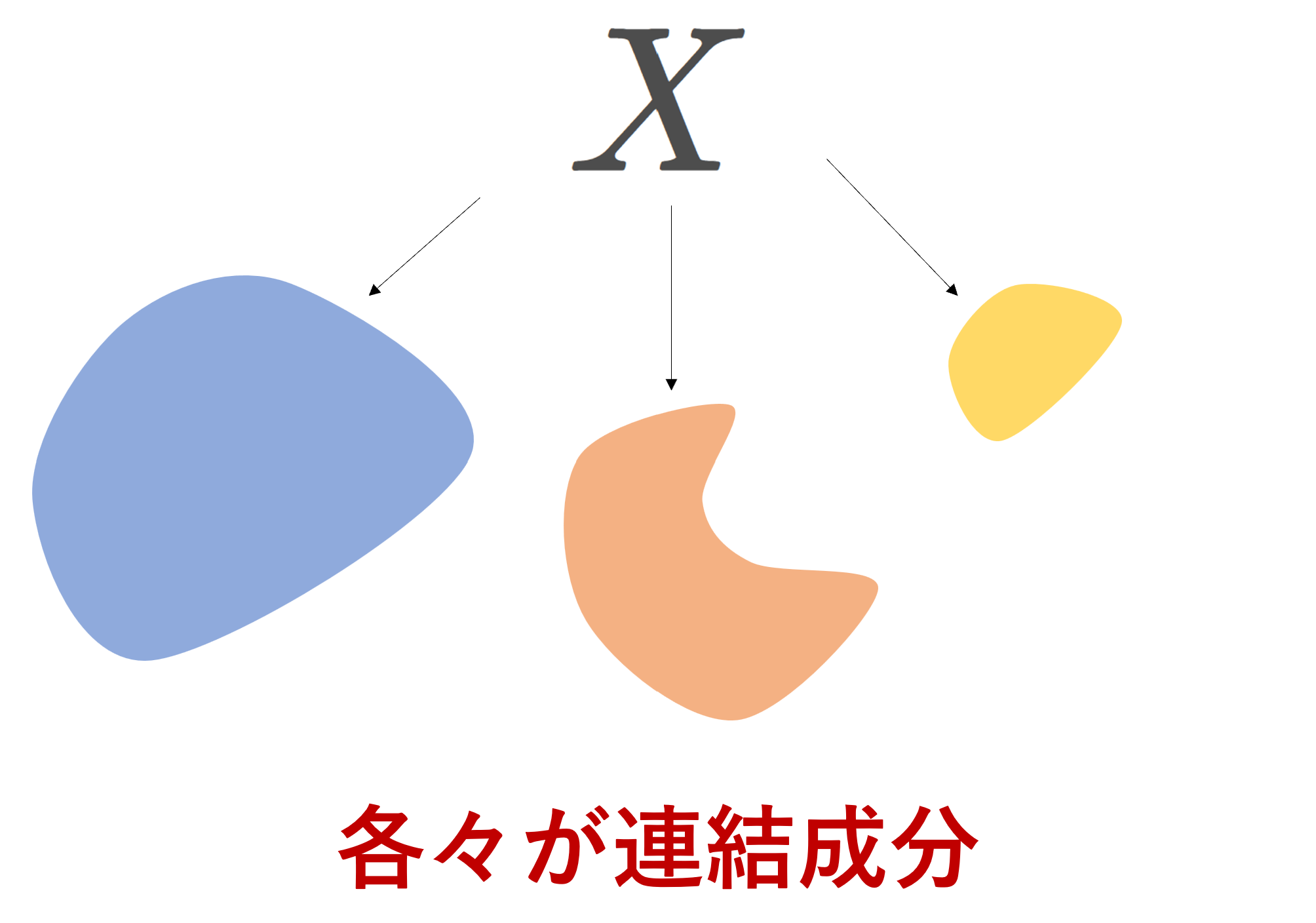
連結性に関連する概念
連結性に関連する諸概念を列挙しておきましょう。
| 名称 | 定義 |
|---|---|
| 連結 (connected) | 2つの互いに素な空でない開集合 U,V で, U\cup V=X となっているものは存在しない |
| 弧状連結 (path connected) | 任意の異なる2点 x,y\in X について,ある連続写像 f\colon [0,1]\to X で, f(0)=x, f(1)=y となるものが存在する |
| 弧連結 (arc connected) | 上の f として,埋め込みすなわち f\colon [0,1]\to f([0,1]) が同相となっているものが常に取れる(※[1]では単に全単射なものが取れるとしている。 X がハウスドルフ ( T_2)なら弧状連結と弧連結は同値) |
| hyperconnected | 任意の空でない2つの開集合が常に共通部分を持つ |
| ultraconnected | 任意の空でない2つの閉集合が常に共通部分を持つ |
| 完全不連結 (totally disconnected) | 連結部分集合が1点集合のみ |
| 完全弧状不連結 (totally path disconnected) | 弧状連結部分集合が1点集合のみ |
| 局所連結 (locally connected) | 全ての点において,連結集合からなる基本近傍系を持つ |
| 局所弧状連結 (locally path connected) | 全ての点において,弧状連結集合からなる基本近傍系を持つ |
| 単連結 (simply connected) | f(0)=f(1) をみたす任意の連続写像 f\colon [0,1]\to X が定値写像とホモトピック |