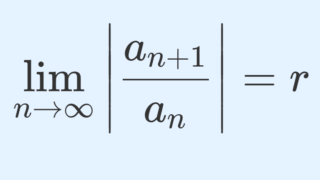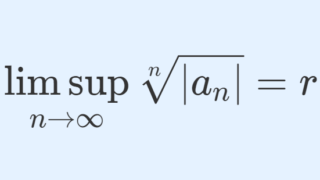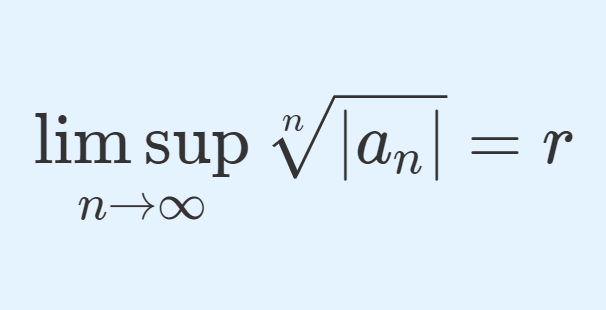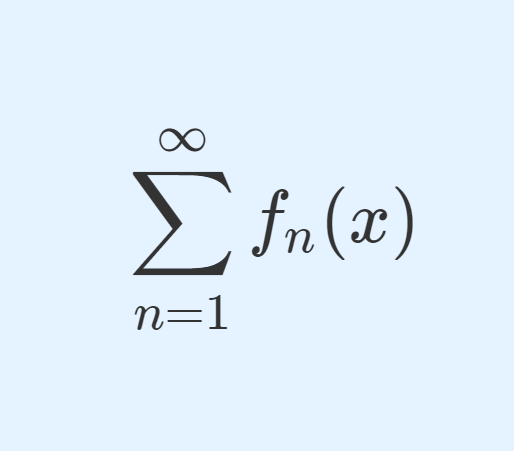級数の収束判定,すなわち級数が収束する十分条件において,重要なものとして「コーシーの収束判定法」と「ダランベールの収束判定法」が取り上げられることがあります。
これらについて,コーシーの判定法はダランベールの判定法より適用範囲が広いことが知られています。これは言い換えると,ダランベールの判定法が使える級数は全てコーシーの判定法が使える(ダランベール \implies コーシーである,包含関係で書くとダランベール \subset コーシーである)ことを意味します。
この定理について紹介し,「ダランベール \implies コーシー」を示す具体例や,コーシーは使えるがダランベールは使えないような具体例を述べましょう。
復習
まず,二つの収束判定法がどのようなものであったか復習したいと思います。
ダランベールの収束判定法
まずは最も有名だと思われる,「ダランベールの収束判定法」の主張から確認します。これは,以下のようなものです。
定理(ダランベールの収束判定法; d’Alembert’s ratio test)
数列 \{a_n\} に対し,
\lim_{n\to\infty} \left| \frac{a_{n+1}}{a_n} \right| = rが存在するとする。このとき, \sum_{n=1}^\infty a_n の収束・発散について
- 0 \le r < 1 ならば絶対収束
- r > 1 ならば発散
となる。
ダランベールの判定法は2項間の比を見ているだけなので,多くの数列において非常に計算しやすいのが強みです。しかし,コーシーの判定法より適用範囲が狭いです。
ダランベールの判定法そのものに関しては,以下の記事に詳しく書かれていますので,参照してください。
コーシーの収束判定法
「コーシーの収束判定法」の方の主張も確認してみましょう。
定理(コーシーの収束判定法; Cauchy’s root test)
数列 \{a_n\} に対し,
\lim_{n\to\infty} \sqrt[n]{|a_n|}= rが存在するとする。このとき, \sum_{n=1}^\infty a_n の収束・発散について
- 0 \le r < 1 ならば絶対収束
- r > 1 ならば発散
となる。
実際は \lim の部分は \limsup でも構いませんが,簡単のため \lim としました。
コーシーの判定法は,一つの項しか見ていない点が強みです。また,実際は \limsup でも良く, \limsup は必ず存在するため,例えば条件収束する場合は必ず \limsup_{n\to\infty} \sqrt[n]{|a_n|} = 1 でなければならない等,そういったことまで分かります。
コーシーの判定法そのものに関しては,以下の記事に詳しく書かれているため,参照してください。
主定理とその証明~ダランベール ⇒ コーシー~
さて,コーシーはダランベールより適用範囲が広いこと,すなわち「ダランベール \implies コーシー」であることを考えていきましょう。
主定理
今回の主役の定理は以下です。
定理(ダランベール \Longrightarrow コーシー)
\lim_{n\to\infty} \left| \frac{a_{n+1}}{a_n} \right| = rとすると,
\lim_{n\to\infty} \sqrt[n]{|a_n|}= rが成立する。ただし, 0 \le r \le \infty とする。
上の式がダランベールで扱った式であり,下の式がコーシーで扱った式ですね。
これが証明できれば,ダランベールが成り立つ級数においてコーシーが成り立つ,すなわちコーシーの収束判定法が適用できることになるわけです。
証明
早速証明しましょう。
証明
0 < r < \infty のとき
\varepsilon \in (0, r) とする。
\lim_{n\to\infty} |a_{n+1}/a_n| = r より,ある N \ge 1 が存在して,
となる。言い換えると, n \ge N のとき,
(r- \varepsilon)|a_n|< |a_{n+1}| < (r + \varepsilon)|a_n|である。帰納的に n \ge 1 のとき,
\begin{aligned} &(r-\varepsilon)^n |a_N| \\ < \,&\cdots \\ < \,&(r-\varepsilon)^2 |a_{N+n-2}| \\ <\,&(r- \varepsilon)|a_{N+n-1}|\\ <\,& |a_{N+n}| \\ <\, &(r + \varepsilon)|a_{N+n-1}| \\ <\, &(r+\varepsilon)^2 |a_{N+n-2}| \\ <\,& \cdots \\ <\, &(r+\varepsilon)^n |a_N|. \end{aligned}従って,
\begin{aligned} \sqrt[N+n]{(r- \varepsilon)^n|a_N|} &< \sqrt[N+n]{|a_{N+n}|} \\ &< \sqrt[N+n]{(r + \varepsilon)^n|a_N|} \end{aligned}となる。 a_n \ne 0 \,\,(n\ge N) に注意して,
\begin{aligned} \sqrt[N+n]{(r\pm\varepsilon)^n|a_N|} &= (r\pm\varepsilon)^{n/(N+n)} |a_N|^{1/N+n} \\ &\xrightarrow{n\to\infty} r\pm\varepsilon \end{aligned}であるから,
\begin{gathered} \liminf_{n\to\infty}\sqrt[n]{|a_{n}|} \ge r-\varepsilon, \\ \limsup_{n\to\infty}\sqrt[n]{|a_{n}|} \le r+\varepsilon. \end{gathered}\varepsilon \to 0+ として \lim_{n\to\infty}\sqrt[n]{|a_{n}|} = r を得る。
r=0 のとき
上の議論おいて,下から r - \varepsilon で抑えるのではなく,0 で抑えれば同様である。
r=\infty のとき
上の議論おいて,下から r - \varepsilon で抑えるのではなく,十分大きな数M で抑えて,M \to \infty とすれば同様である。
証明終
具体例
「ダランベールが適用できる例(よってコーシーも適用できる例)」と,「ダランベールは適用できないがコーシーが適用できる例」をそれぞれ挙げましょう。
ダランベールが適用できる例
例1.
\textcolor{red}{a_n = \log n / 2^n } とする。このとき,
\begin{aligned} \lim_{n\to\infty} \frac{\log( n+1) / 2^{n+1}}{\log n / 2^n} &= \lim_{n\to\infty} \frac{\log(n+1)}{2\log n} \\ &= \frac{1}{2} < 1 \end{aligned}より,ダランベールの判定法が使えて絶対収束する。一方,
\begin{aligned} \lim_{n\to\infty} \sqrt[n]{\frac{\log n}{2^n}} &= \lim_{n\to\infty}\frac{(\log n)^{1/n}}{2} \\ &= \frac{1}{2} < 1 \end{aligned}より,コーシーの判定法も使えて絶対収束する。
ダランベールが適用できないが,コーシーが適用できる例
例2.
\textcolor{red}{a_n = (2+(-1)^n)/ 2^n } とする。このとき,
\begin{gathered} \limsup_{n\to\infty} \frac{(2+(-1)^{n+1})/ 2^{n+1}}{(2+(-1)^n)/ 2^n} = \frac{3}{2}, \\ \liminf_{n\to\infty} \frac{(2+(-1)^{n+1})/ 2^{n+1}}{(2+(-1)^n)/ 2^n} = \frac{1}{6} \end{gathered}より,ダランベールの判定法は使えない。一方,
\begin{aligned} \lim_{n\to\infty} \sqrt[n]{\frac{2+(-1)^n}{2^n}} = \frac{1}{2} < 1 \end{aligned}より,コーシーの判定法は使えて絶対収束する。
実際のところこの例は, (2+(-1)^n)/ 2^n \le 3/2^n と上から抑えてして比較判定法を用いるのが最も簡明だと思います。
コーシーもダランベールも適用できない例は,それすなわちコーシーが適用できない例になるため,以下の記事の具体例を参照してください。