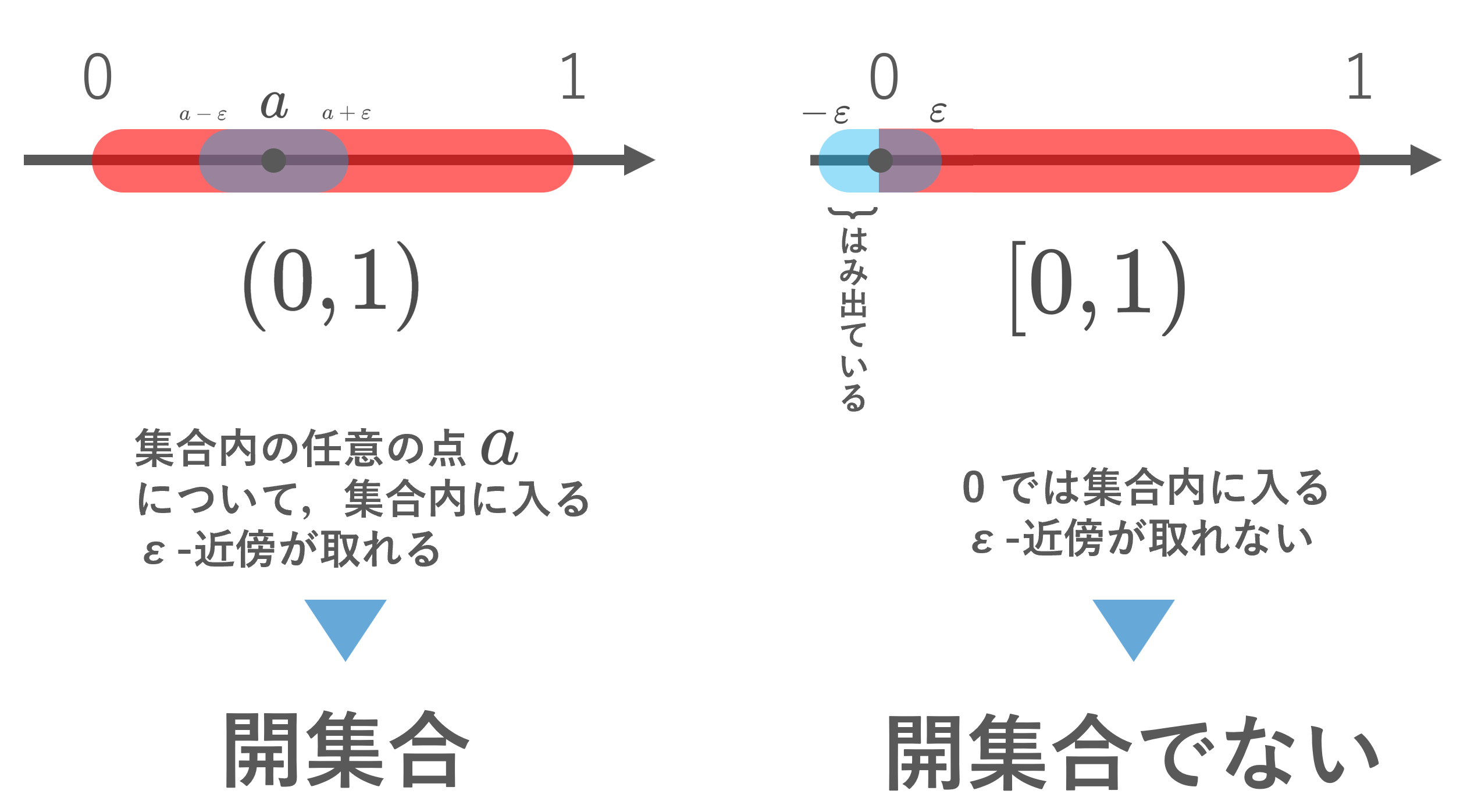
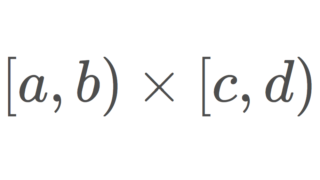位相空間論における相対位相とは，位相空間の部分集合に入る位相のことです。元の位相と同じ性質を引き継ぐこともあれば，全く異なる性質を持つこともあります。相対位相・部分位相空間について，その定義と具体例・性質とその証明をしていきます。
相対位相と部分位相空間の定義
定義（相対位相と部分空間）
(X,\mathcal{O}) を位相空間とする。 A\subset X を空でない部分集合とする。
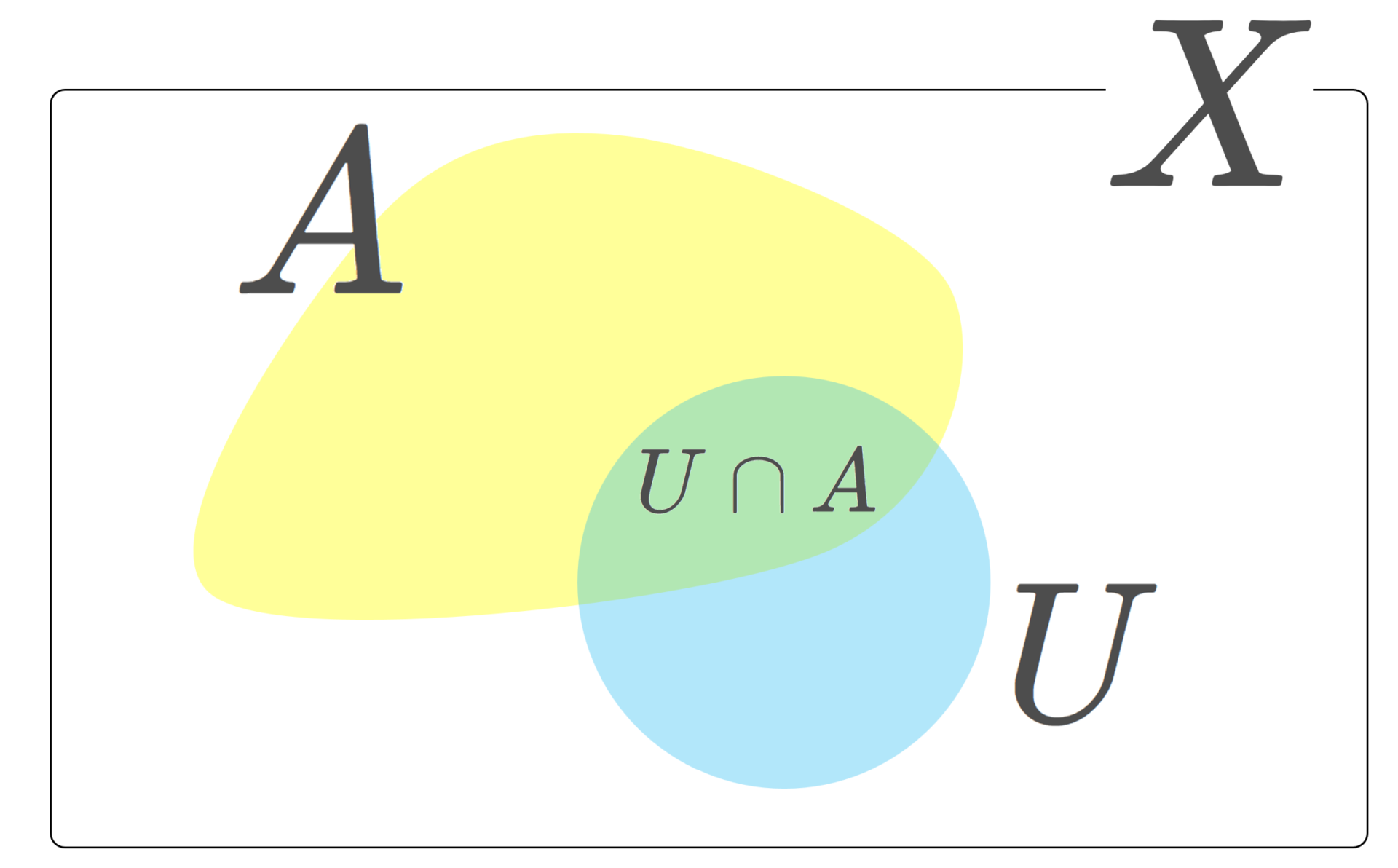
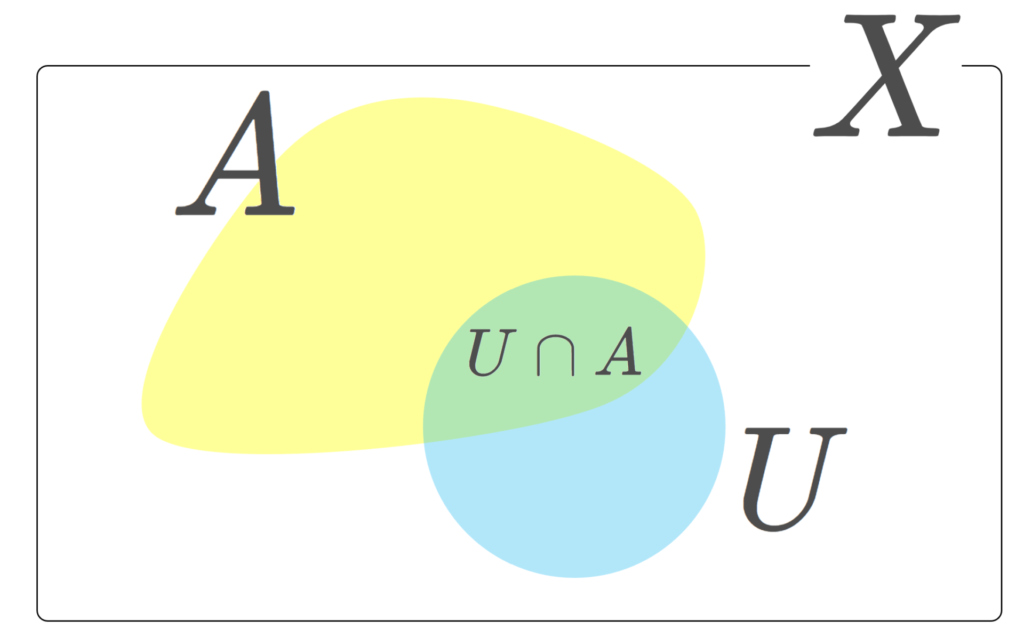
\Large\color{red}\mathcal{O}_A =\{U\cap A\mid U\in\mathcal{O}\}
とすると， (A,\mathcal{O}_A) は位相空間になる。これを A 上の相対位相 (relative topology) といい， (A,\mathcal{O}_A) は X の部分空間 (subspace) または部分位相空間 (topological subspace) という。
また， \mathcal{F} = \{ X\setminus U \mid U\in\mathcal{O}\} を X の閉集合族とすると，(A,\mathcal{O}_A) の閉集合族は
\Large \color{red} \mathcal{F}_A = \{ F\cap A \mid F\in \mathcal{F}\}
となります。実際， F\cap A = (X\setminus U)\cap A = A\setminus (U\cap A) となることから証明できます。
相対位相と部分位相空間の具体例5つ
例1.
(0,1]\subset \R に， \R の相対位相を入れた空間を考える。このとき，
- (0,1] は開集合かつ閉集合である
- (a,1]\;\; (0\le a<1) は開集合である
- (0, b]\;\; (0<b\le 1) は閉集合である
- (a, b) \;\; (0\le a<b\le 1) は開集合である
- [a, b] \;\; (0< a<b\le 1) は閉集合である
(0, 1] は \R の部分集合としては開集合でも閉集合でもありませんが，(0,1] を全体集合とした部分空間としては，開集合かつ閉集合です。
2.は， (a,1] = (a,2)\cap (0,1] とかけ， (a,2) は \R における開集合のため，正しいです。もちろん， (a,1] は \R における開集合ではありません。
3.は， (0,b] = [0,b] \cap (0,1] とかけ， [0,b] は \R における閉集合のため，正しいです。もちろん， (0,b] は \R における開集合ではありません。
このように，相対位相では，元の空間では開集合や閉集合でなかったものが，開集合や閉集合になることがあります。
例2.
整数全体の集合 \mathbb{Z}\subset \R に \R の相対位相を入れると，離散位相となる。
離散位相とは，すべての部分集合が開集合になるような位相空間です。 n \in \mathbb{Z} に対し， \{n\} = (n-1/2, n+1/2)\cap \mathbb{Z} ですから，すべての1点集合は開集合です。
例3.
[0,1]\cup [2,3]\subset \R に \R の相対位相を入れると，
- [0,1], [2,3] は開集合かつ閉集合である。特に，この部分空間は連結でない
[0,1]=(-1, 3/2)\cap ( [0,1]\cup [2,3]) ですから， [0,1] は開集合です。 [2,3] も同様です。
例4.
有理数全体の集合 \mathbb{Q}\subset \R に \R の相対位相を入れると，
- (0,1)\cap \mathbb{Q} は開集合だが閉集合でない
- (0,\sqrt{2})\cap \mathbb{Q} は開集合だが閉集合でない
- (\sqrt{2},\sqrt{3})\cap\mathbb{Q} は開集合かつ閉集合である。特に，この部分空間は連結でない
- \{q\}\;\;(q\in\mathbb{Q}) は閉集合だが開集合でない。特に，この相対位相は離散位相ではない
3.については， (\sqrt{2},\sqrt{3})\cap\mathbb{Q}= [\sqrt{2},\sqrt{3}]\cap\mathbb{Q} ですから，開集合かつ閉集合ですね。
例5.
S^1=\{ (x, y)\in\R^2\mid x^2+y^2=1\} に， \R^2 の相対位相を入れた空間を考える。このとき，
- \{ (x, y)\in S^1 \mid y>0\} は開集合だが閉集合でない
- \{ (x, y)\in S^1 \mid y\ge 0\} は閉集合だが開集合でない
\R^2 においては，1.は開集合ではないです。一方で2.は \R^2 においても閉集合です。
相対位相と部分位相空間の性質5つとその証明
続いて，相対位相の性質を見ていきましょう。
1. 相対位相と誘導される位相の関係
定理1（誘導される位相）
(X, \mathcal{O}) を位相空間とし， A\subset X とする。さらに， i\colon A\to X を包含写像とする。このとき， i から誘導される A の位相は A の相対位相と一致する。
証明
i から誘導される位相は \{ i^{-1}(U)\mid U\in \mathcal{O}\} と書けるが， i^{-1}(U)= U\cap A なので，これは相対位相の定義に一致している。
証明終
2. 相対位相と開集合・閉集合
定理2（相対位相と開集合・閉集合）
(X, \mathcal{O}) を位相空間とし， (A, \mathcal{O}_A) をその部分空間とする。このとき，
- B\subset A が X における開集合(閉集合)ならば A においても開集合(閉集合)である。
- A が開集合であるとき， B\subset A が A における開集合ならば， X においても開集合である。
- A が閉集合であるとき， B\subset A が A における閉集合ならば， X においても閉集合である。
- B\subset A について， \overline{B}^A = \overline{B}^X\cap A である。ここで， \overline{B}^A, \overline{B}^X はそれぞれ， B の A, X の位相における閉包を表す。
なお，上の具体例でみたように，一般には A における開集合・閉集合が X においても開集合・閉集合になるとは限りません。
以下で， X, A における閉集合系をそれぞれ \mathcal{F}, \mathcal{F}_A と書くことにします。
証明
1.について
B\in \mathcal{O} とすると， B= B\cap A\in\mathcal{O}_A なので， B は A における開集合である。
また， B\in \mathcal{F} とすると， B= B\cap A\in\mathcal{F}_A なので， F は A における閉集合である。
2.について
B\in \mathcal{O}_A とすると，ある U\in\mathcal{O} が存在して， B = U\cap A とできる。いま， A\in\mathcal{O} という仮定があるから， B\in \mathcal{O} である。よって， B は X においても開集合である。
3.について
2.の \mathcal{O}, \mathcal{O}_A を \mathcal{F},\mathcal{F}_A に置き換えれば同様である。
4.について
相対位相の定義の直後の解説により，\overline{B}^X\cap A は A における閉集合である。また， B\subset \overline{B}^X\cap A であるから，
\overline{B}^A \subset \overline{B}^X\cap A
である。一方で同じく相対位相の定義の直後の解説により， \overline{B}^A = F\cap A となる X の閉集合 F が存在する。 \overline{B}^A \supset B\cap A であるから， F\supset B である。ゆえに F\supset \overline{B}^X なので，
以上から， \overline{B}^A = \overline{B}^X\cap A が示せた。
証明終
3. 相対位相の相対位相
定理3（相対位相の相対位相）
(X, \mathcal{O}) を位相空間とし， B\subset A\subset X，さらに (A, \mathcal{O}_A) を X の部分空間とする。このとき，
B を A の部分空間とみたときの相対位相と， X の部分空間とみたときの相対位相は一致する。すなわち，
\Large\color{red} (\mathcal{O}_A)_B = \mathcal{O}_B
である。
証明
(\mathcal{O}_A)_B\subset \mathcal{O}_B について
W\in (\mathcal{O}_A)_B とすると，ある V\in \mathcal{O}_A が存在して，W = V\cap B と表せる。また，ある U\in\mathcal{O} が存在して， V = U\cap A と表せるため，
W = U\cap A\cap B = U\cap B \in \mathcal{O}_B
よって (\mathcal{O}_A)_B\subset \mathcal{O}_B である。
\mathcal{O}_B\subset (\mathcal{O}_A)_B について
W\in\mathcal{O}_B とすると，ある U\in\mathcal{O} が存在して， W = U\cap B と表せる。これは，
\begin{aligned} W &= U\cap B= U\cap (A\cap B)\\&= (U\cap A)\cap B \in( \mathcal{O}_A)_B \end{aligned}
であるため， \mathcal{O}_B\subset (\mathcal{O}_A)_B である。
証明終
4. 相対位相と連続写像
定理4（相対位相と連続写像）
( X, \mathcal{O}_X), (Y, \mathcal{O}_Y) を位相空間とし， A\subset X を部分空間とする。 f\colon X\to Y を連続写像とするとき，
証明
1.について
V\in \mathcal{O}_Y とすると， f は連続より， f^{-1}(V)\in \mathcal{O}_X である。ここで，
{f|_A}^{-1}(V)=f^{-1}(V)\cap A
であり，後者は部分空間 A における開集合であるから， f|_A は連続である。
2.について
部分空間 f(X)\subset Y における開集合は V\in\mathcal{O}_Y を用いて V\cap f(X) とかける。これは，
\begin{aligned} f^{-1} (V\cap f(X)) &= f^{-1}(V) \cap f^{-1}(f(X))\\&= f^{-1}(V)\cap X\\&= f^{-1}(V) \in\mathcal{O}_X\end{aligned}
となるため， f\colon X\to f(X) は連続である。
証明終
5. 相対位相によって保たれる性質・保たれない性質
定理5（相対位相によって保たれる性質）
(X, \mathcal{O}) を位相空間とし， (A, \mathcal{O}_A) をその部分空間とする。
証明
1.について
x, y\in A を異なる2点とする。 X はハウスドルフ空間だから，ある開集合 U, V\in\mathcal{O} で
x\in U, \, y\in V,\, U\cap V=\emptyset
とできる。 U_A = U\cap A, \, V_A=V\cap A とすると， U_A, V_A\in \mathcal{O}_A であり，
であるから， A もハウスドルフ空間である。
2.について
a\in A に対して，\mathcal{N}(a) を X における a\in X の基本近傍系とすると，
\mathcal{N}_A(a) =\{ N\cap A\mid N\in \mathcal{N}(a)\}
は， A における a\in A の基本近傍系であることが示せる。よってわかる。
3.について
\mathcal{B}\subset\mathcal{O} を X の開基とすると，
\mathcal{B}_A =\{ B\cap A\mid B\in \mathcal{B}\}
は \mathcal{B}_A\subset \mathcal{O}_A であり，A の開基であることが示せる。よってわかる。
4.について
A の開被覆を \mathcal{C}\subset \mathcal{O} とすると，A^c は開集合であるから，\mathcal{C}\cup \{ A^c\} は X の開被覆になる。
X はコンパクトであるから，\mathcal{D}\subset \mathcal{C} が存在して， \mathcal{D}\cup \{ A^c\} は X の有限部分被覆になる。
ここで， \mathcal{D}_A = \{ D\cap A\mid D\in\mathcal{D}\} とすると， \mathcal{D}_A\subset \mathcal{O}_A は A における有限開被覆になる。よって，A はコンパクトである。
5.について
D\subset X が X において稠密であるとき， D\cap A が A において稠密であることを示す。
B\subset A を A における開集合とする。 A は X における開集合なので，定理2.2より， B も X における開集合である。よって， D\cap B \ne \emptyset であり，
D\cap B = D\cap (A\cap B)=(D\cap A)\cap B
なので， (D\cap A)\cap B\ne\emptyset となる。ゆえに， D\cap A は A において稠密であることが示せた。 D を可算集合と思うと， D\cap A も高々可算集合なので，示せた。
証明終
定理5とは逆に，相対位相によって保たれない性質も紹介しましょう。
定理5のとおり，1.は A が閉集合でないと成り立たないし，2.は A が開集合でないと成り立ちません。
1.については， (0,1)\subset \R に，通常の \R から定まる相対位相を入れたものが反例になります。\{ (0, 1-1/n)\} は (0,1) における開被覆ですが，有限部分被覆は存在しません。
2.については，ゾルゲンフライ平面 \R^2 とその部分空間 \Delta= \{ (x,-x)\mid x\in \R\} があげられます。ゾルゲンフライ平面とは，
\{ [a,b)\times [c,d) \mid a,b,c,d\in\R\}
を開基とする位相空間 \R^2 のことです。この位相空間は可分ですが，部分空間 \Delta は離散空間となり，集合として非可算集合なので，可分ではありません。ゾルゲンフライ平面については，そのうち別の記事で詳しく紹介することにしましょう。
3.については例えば， (0,1)\cup (2,3)\subset \R に，通常の \R から定まる相対位相を入れたものが反例になります。 (0,1), (2,3) が相対位相における開集合ですので， \R は連結ですが， (0,1)\cup (2,3) は連結ではありません。
