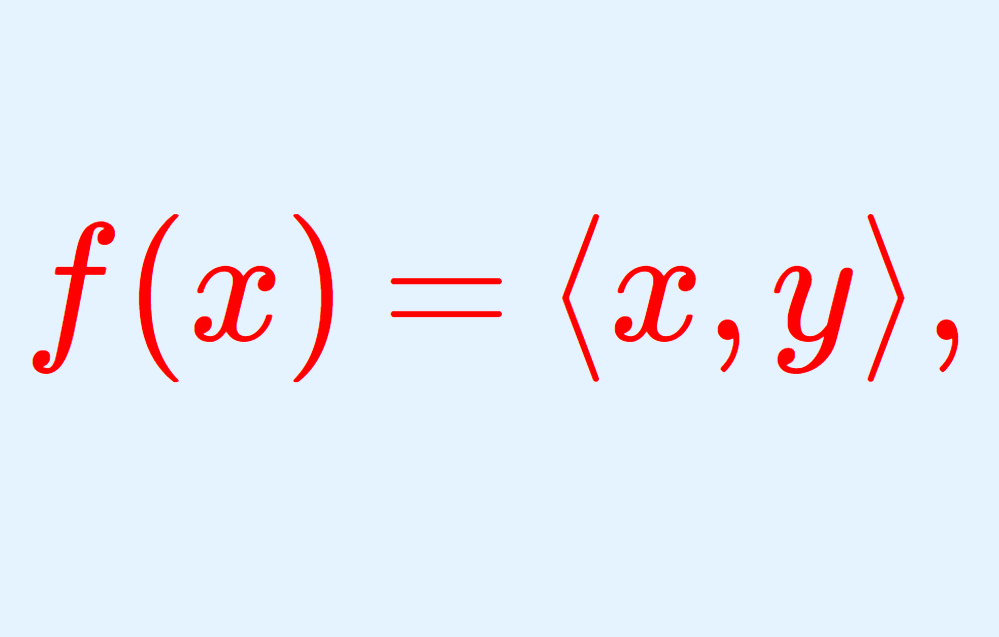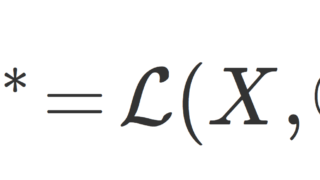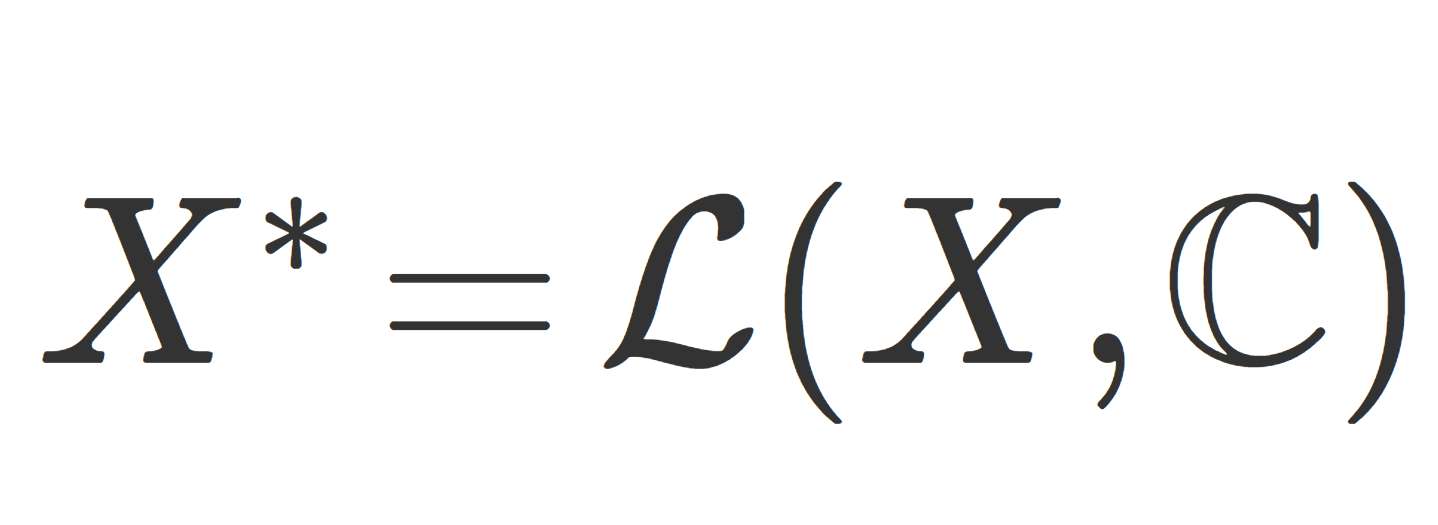リースの表現定理とは,ヒルベルト空間上の有界線形汎関数は,内積の形で書けるということを主張する定理です。
リースの表現定理について,その主張と証明を紹介し,さらにその帰結として,ヒルベルト空間とその双対空間はある意味「同一視」できることを証明します。
リースの表現定理とその証明
本記事では, x,y の内積を \langle x, y\rangle と表記します。
リースの表現定理 (Riesz’s representation theorem)
H をヒルベルト空間とし, H^* をその双対空間(有界線形汎関数全体のなす空間)とする。このとき,任意の f\in H^* に対し,ある y\in H が一意的に存在して,
\Large \color{red}f(x)=\langle x, y\rangle ,\quad x\in H
とできる。
ヒルベルト空間上の有界線形汎関数は,常に内積の形で書けるということですね。証明しましょう。
証明
f=0 なら, y=0 とすればよい。 f\in H^*\setminus\{0\} のとき
N=\operatorname{Ker} f と定める(→Kernel)と, N\subsetneq H であり, f の連続性から N は閉部分空間である。射影定理より, H=N\oplus N^\perp である。 y'\in H^\perp を f(y')=1 となるようにとる。このとき, x\in H に対し, x-f(x)y'\in N なので, x-f(x)y' \perp y' に注意して,
\begin{aligned}\langle x, y'\rangle &= \langle x-f(x)y'+f(x)y' , y\rangle \\ &= \langle f(x)y' , y' \rangle =f(x)\|y'\|_H^2 .\end{aligned}
ゆえに, y=y'/\|y'\|^2_H と定めると, \langle x,y\rangle =f(x) となる。
y の一意性を示す。一意でないとして,y_1,y_2\in H が f=\langle \cdot, y_1\rangle=\langle \cdot, y_2\rangle をみたすなら, \langle \cdot ,y_1-y_2\rangle は零写像であるが, \langle y_1-y_2, y_1-y_2\rangle =\|y_1-y_2\|^2\ne 0 に矛盾する。
証明終
なお,証明中の N^\perp は一次元空間になります。これは,\mathbb{C} が一次元空間であることが密接に関係しています。
リースの表現定理からの帰結
定理( H\simeq H^*)
H を \mathbb{C} 上のヒルベルト空間とする。 \Phi\colon H\to H^* を \Phi(y) = \langle \cdot, y\rangle と定めると,これは以下の意味で H から H^* への等長反同型(等長共役同型)となる。
- \Phi(ax+by) =\overline{a}\Phi(x)+\overline{b}\Phi(y), \quad x,y\in H, \, a,b\in \mathbb{C}
- \Phi は全単射
- \|\Phi(y)\|_{H^*} = \|y\|_H
ヒルベルト空間は双対空間と内積が「同じようなもの」ということです。非常に良い性質を持っていることが分かると思います。
なお,定理は \mathbb{C} 上のヒルベルト空間としていますが,\R 上のときは, H と H^* は等長同型といえます。
証明
1.は確認すればわかる。2.について,全射性はリースの表現定理よりよい。単射性は3.と線形写像が単射になる必要十分条件は核(Ker)が0になる証明よりよい。
3.を示す。 x\in H に対し,コーシーシュワルツの不等式より,
\|\Phi(y)(x)\| = |\langle x, y \rangle| \le \|x\|\|y\| .
両端辺 \sup_{\|x\|=1} をとると \|\Phi(y)\|\le \|y\| となる。一方で,
も成り立つから, \|\Phi(y)\|=\|y\| となる。
証明終
この定理より,特に H= H^{**} も分かりますから,ヒルベルト空間は回帰的(反射的)といえます。