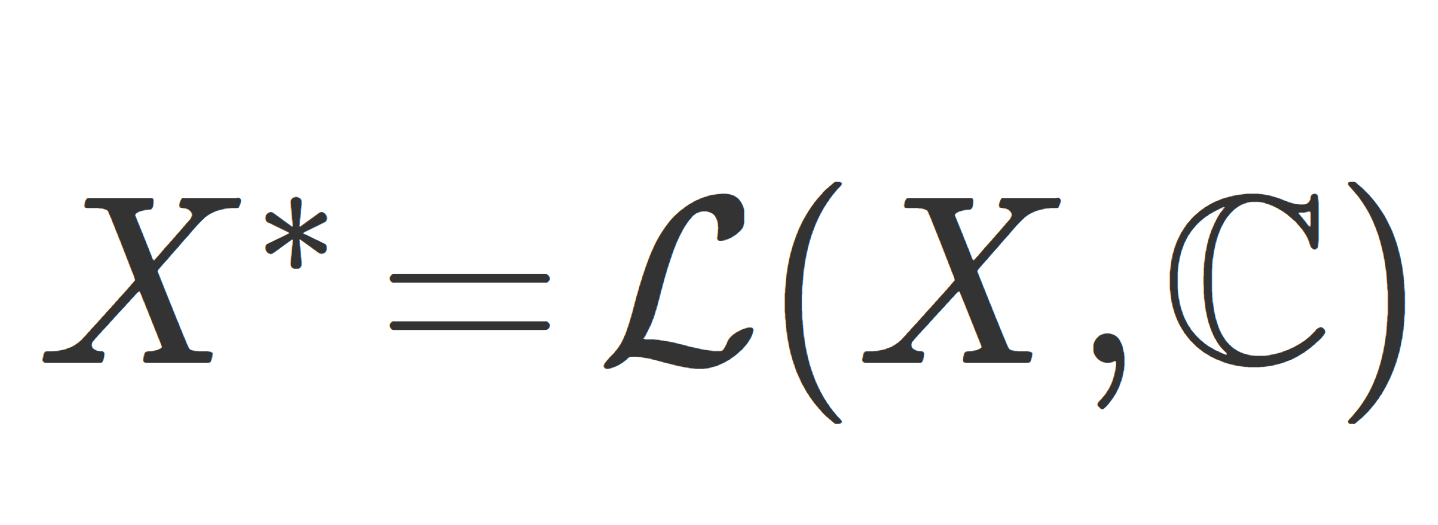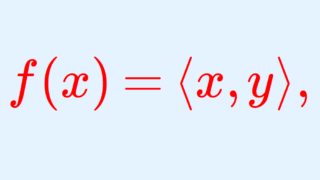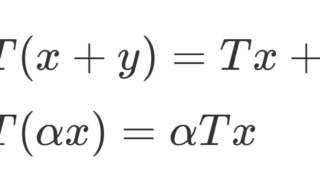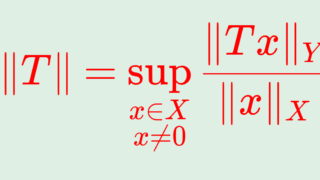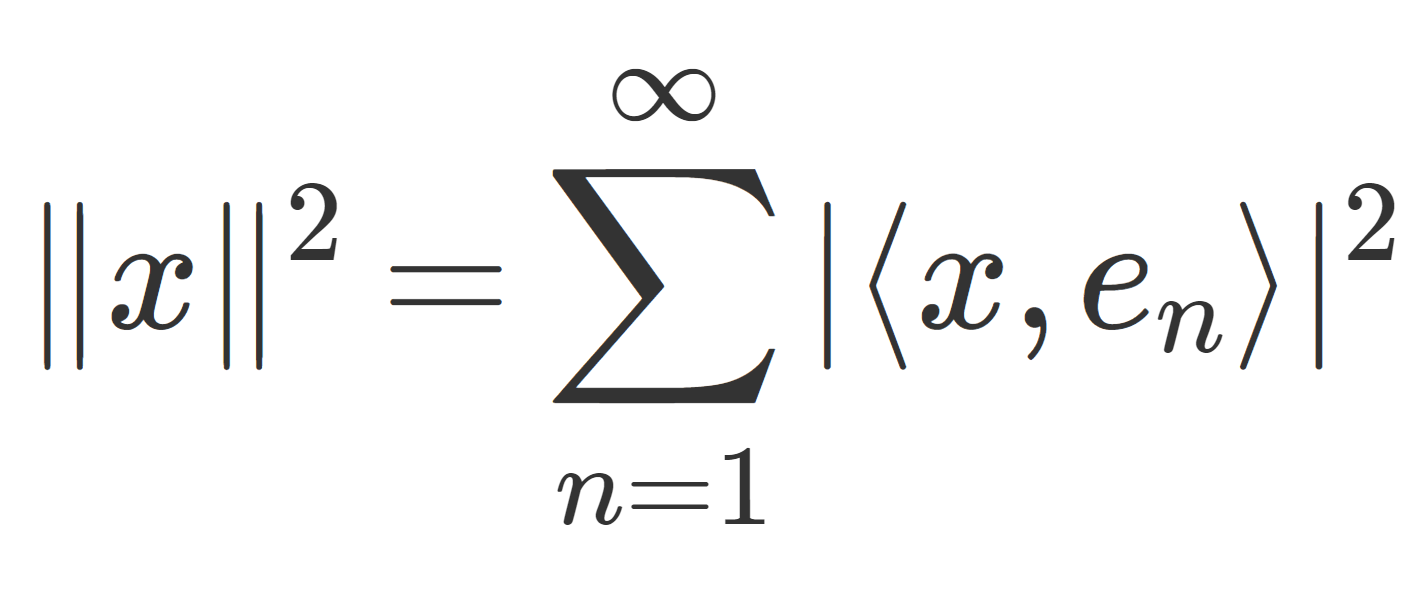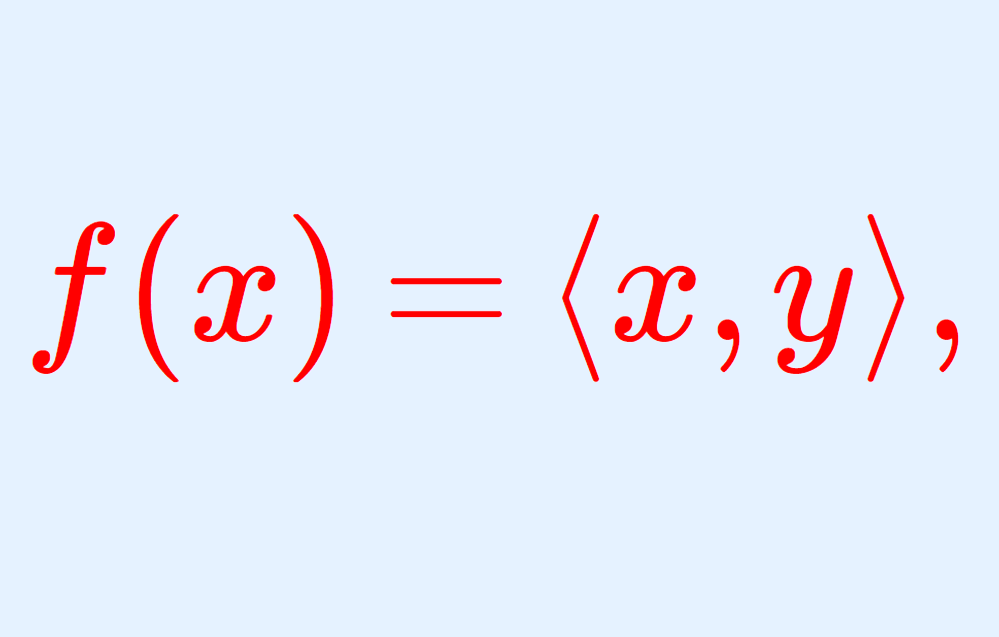双対空間あるいは共役空間とは,体 K 上のベクトル空間(ノルム空間)から, K への線形写像全体のなすベクトル空間のことで,線形汎関数は双対空間の元のことを言います。
双対空間を考えることで,もとのベクトル空間の性質を調べるのに役に立ちます。「双対」という言葉からわかるように,もとのベクトル空間と「対」になっていると考えることができたりするからです。
双対空間(共役空間)と有界線形汎関数について,理解していきましょう。
双対空間(共役空間)と有界線形汎関数
双対空間(共役空間)と有界線形汎関数を理解するには,有界線形作用素全体の空間を理解せねばなりません。詳しくは線形作用素とその有界性について詳しくや作用素ノルムとは~定義と具体例と性質~で説明していますが,軽く要約しておきましょう。
上の Y を \mathbb{C} に置き換えたものを特別扱いします。
定義(双対空間・線形汎関数)
X を \mathbb{C} 上ノルム空間とする。このとき, \color{red} \large \mathcal{L}(X,\mathbb{C}) を双対空間 (dual space) または共役空間 (conjugate space) といい,その元を有界線形汎関数 (bounded linear functional) という。
また, \mathcal{L}(X,\mathbb{C}) は略して \large \color{red} X^* と書かれることが多い。
\mathbb{C} は \|z\| = |z| であるバナッハ空間ですから,( X がバナッハ空間かどうかにかかわらず,) X^* はバナッハ空間になります。
有界線形汎関数 f\in X^* と x\in X に対して, f(x) を \color{red} \langle f, x\rangle などとかくことがあります。内積に見えますが,内積に見えた方が都合がよいことがあるのです(実際,内積の性質にある意味似ており,ノルム空間でも内積のようなものを考えられるようになる)。
なお,今回は \mathbb{C} 上としましたが, \R 上のノルム空間の場合は X^*=\mathcal{L}(X,\R) と考えます。
X^* に対して,さらにその双対空間 X^{**}=\mathcal{L}(X^*,\mathbb{C}) やさらに X^{***} を考えることも可能です。
双対空間(共役空間)と線形汎関数の例
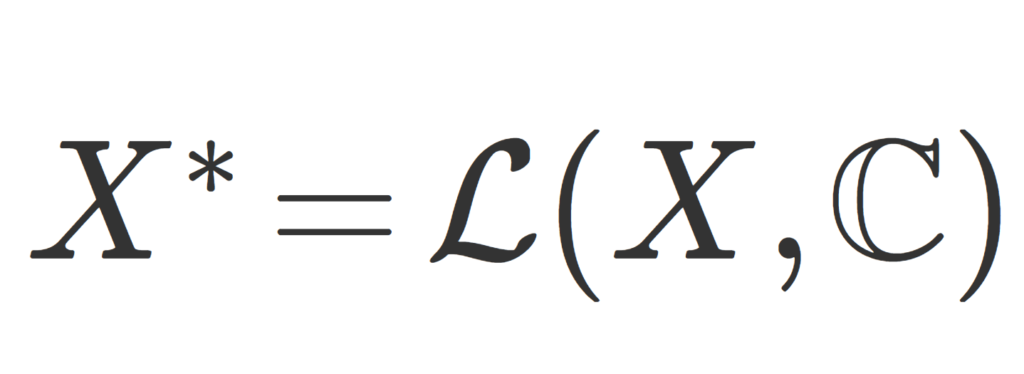
例1.
連続関数 f\colon [0,1] \to \mathbb{C} 全体の集合のなす空間 C[0,1] に対し, \varphi\colon C[0,1]\to \mathbb{C} を
\varphi(f) = f(0),\quad f\in C[0,1]
と定めると, \varphi \in C[0,1]^* である。さらに, \|\varphi\| = 1 である。また, \psi\colon C[0,1]\to \mathbb{C} を
と定めると, \psi \in C[0,1]^* である。さらに, \|\psi\| = 1 である。
C[0,1] の空間には,ノルム \|f\| = \sup_{0\le x\le 1} |f(x)| が定まっているとします。このとき, f\equiv 1 とすると, \|\varphi(f)\|=1 であり,また,明らかに \| \varphi(f)\| =|f(0)|\le \|f\| なので,結局 \|\varphi\|=1 ですね。
\psi も同様に \|\psi\|=1 が示せるので考えてみてください。
例2.
\mathbb{C}^2= \left\{\begin{pmatrix}a\\b \end{pmatrix}\middle | a,b\in \mathbb{C}\right\}
に対し,
である。要するに, (k,l) \in (\mathbb{C}^2)^* に対し,
と考える。
実際, f\in (\mathbb{C}^2)^* としましょう。 e_1=\begin{pmatrix}1\\0\end{pmatrix},e_2=\begin{pmatrix}0\\1 \end{pmatrix} と略記すると, f は (f(e_1), f(e_2)) のように行列表示できますから,
(\mathbb{C}^2)^*\subset \left\{(k,l)\middle | k,l\in \mathbb{C}\right\}
です。逆の包含は明らかですから,結局例2.の事実が言えました。
例3( L^p, \ell^p 空間)
1<p,q<\infty は 1/p+1/q=1 をみたすとする。このとき,ある種の同一視により,
- L^p(\R)^* =L^q(\R)
- {\ell^p}^*= \ell^q
- L^1(\R)^* =L^\infty (\R)
- L^\infty (\R)^* \supsetneq L^1(\R)
詳しい説明は省きます。
双対空間(共役空間)の性質
定理(双対空間(共役空間)の性質)
X をノルム空間とする。
- \dim X = n\implies \dim X^*=n (次元)
- ある意味での同一視により, X\subset X^{**} である。
2.について,特に X=X^{**} が成り立つならば, X は回帰的または反射的 (reflexive) といいます。 X^{**} はバナッハ空間ですから,このとき X もバナッハ空間になります。
2.の証明はハーンバナッハの定理を使っており,簡単ではないです。
証明
1.について X の基底を e_1,e_2,\dots, e_n とする。
1\le i\le n に対し, f_i\in X^* を
f_i(e_j)=\delta_{ij} =\begin{cases} 1 & i=j,\\ 0 & i\ne j \end{cases},\quad 1\le j\le n
と定める( \delta_{ij} はクロネッカーのデルタ)。
とする(右辺は 0\in X^* なので X 上の零写像の意味)。両辺の写像の e_j の行先を考えると, a_j=0 なので, a_1=a_2 =\dots =a_n=0 となる。よって f_1,f_2,\dots, f_n は一次独立である。また, f\in X^* とすると,
とかける。したがって, f_1,f_2,\dots, f_n は X^* における基底である(双対基底 (dual basis))。ゆえに, \dim X^*=n となる。
2.について x\in X を一つ固定する。 f\in X^* に対し, T_x(f) = f(x) により作用素 T_x\colon X^*\to \mathbb{C} を定めると, T_x\in X^{**} である。ここで,
\begin{aligned}\|T_x\|_{X^{**}} &= \sup_{\|f\|_{X^*}=1} |T_x(f)| \\ &= \sup_{\|f\|_{X^*}=1} |f(x)|\\ &\le \sup_{\|f\|_{X^*}=1} \|f\|_{X^*} \|x\|_X \\ &= \|x\|_X. \end{aligned}
また,ハーンバナッハの拡張定理の系より, x\ne 0 なら f(x)=\|x\|_X かつ \|f\|_{X^*}=1 をみたす f\in X^* が存在するから,
したがって, \|T_x\|_{X^{**}} = \|x\|_X である。ゆえに, X\supset x\mapsto T_x\subset X^{**} によって, X\subset X^{**} と考えることができる。
証明終
リースの表現定理
H をヒルベルト空間とします。このとき,任意の f\in H^* に対し,ある y\in H が存在して,
f(x)=\langle x,y\rangle ,\quad x\in H
が成立します。すなわち, f \in H^* はある y\in H を用いて表現できるということであり, ある意味 \color{red}H\simeq H^* と考えられるということです。これを,リースの表現定理 (Riesz’s representation theorem) といいます。詳しくは以下で解説しています。