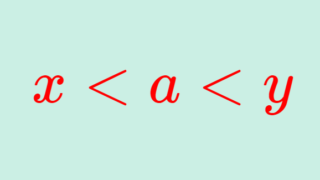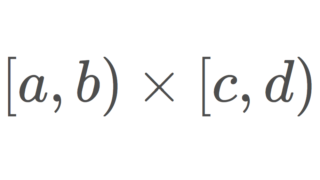【位相空間】稠密性と可分性～定義と具体例～

位相空間の部分集合が，稠密（ちゅうみつ）であるとは，閉包が全体集合に一致することを言い，可分であるとは，高々可算な稠密部分集合を持つ位相空間のことを言います。

稠密の定義と可分の定義を，それぞれたくさんの具体例を添えて確認していきましょう。

稠密性（ちゅうみつせい）の定義と具体例3個
1. 稠密性の定義
2. 稠密性の具体例
可分性の定義と具体例8個
関連する記事

稠密性（ちゅうみつせい）の定義と具体例3個

まずは稠密性の定義と具体例を述べましょう。

稠密性の定義

定義（稠密）

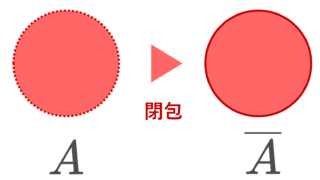
$(X,\mathcal{O})$ を位相空間とし， $A\subset X$ とする。

$A$ が $X$ において稠密 (ちゅうみつ, dense) であるとは，

\Large \color{red}\overline{A}=X

が成り立つことを言う。ただし， $\overline{A}$ は $A$ の閉包を表す。

稠密の「稠」の漢字に注意してください。

定義より， $A\subset B\subset X$ で $A$ が $X$ において稠密なら， $B$ も $X$ において稠密です。また， $X$ は明らかに $X$ において稠密です。

稠密性の具体例

稠密の例1( $\R$ ).

ユークリッド空間 $\R$ において，有理数全体の集合 $\mathbb{Q}\subset \R$ は稠密である。

$\overline{\mathbb{Q}}=\R$ ですから稠密です。有理数の稠密性には，以下の記事でも解説しています。

上の記事では，稠密性の定義を，「任意の開区間が有理数を含む」としていますが。これはすなわち「無理数の部分集合である開集合は空集合以外存在しない」ということなので， $\operatorname{Int}(\R\setminus\mathbb{Q})=\emptyset$ です。ただし， $\operatorname{Int}$ は集合の内部(開核)を指します。これはすなわち， $\overline{\mathbb{Q}}=\R$ ということです。

稠密の例2(密着位相).

$(X,\{ \emptyset, X\})$ を密着空間とする。

このとき，空集合でない全ての部分集合 $A\subset X$ は稠密である。

$\overline{A}=X$ ですから，空集合でない全ての部分集合は稠密になりますね。

稠密の例3(離散位相).

$(X, 2^X)$ を離散空間とする。

このとき， $X$ の稠密部分集合は $X$ に限る。

$A\subset X$ に対し， $\overline{A}=A$ ですからね。

可分性の定義と具体例8個

稠密性の定義を理解していれば，可分性の定義も理解できるはずです。

可分性の定義

定義（可分）

$(X, \mathcal{O})$ を位相空間とする。この位相空間が高々可算な稠密部分集合を持つとき，この位相空間は可分 (separable) や可分空間 (separable space) という。

要するに，可算部分集合 $A\subset X$ が存在して， $\overline{A}=X$ が成り立つとき，可分空間というんですね。可算については，可算集合と非可算集合(可算無限・非可算無限)で解説しています。

可分性の具体例

ここからは，可分空間の具体例を見ていきましょう。

可分の例1( $\R$ ).

ユークリッド空間 $\R$ は通常の位相で可分である。

$\overline{\mathbb{Q}}=\R$ であり，有理数全体の集合 $\mathbb{Q}$ は可算集合なので，可分だとすぐ分かりますね。

可分の例2.

$X$ が高々可算集合であるような位相空間 $(X,\mathcal{O})$ は可分である。

$\overline{X}=X$ であり， $X$ 自体が高々可算なので，可分ですね。

可分の例3(密着位相).

$(X, \{\emptyset, X\})$ を密着空間とすると，この空間は可分である。

$X$ の空でない任意の部分集合が稠密になりますから，可分になります。

可分の例4(離散位相).

離散位相空間 $(X, 2^X)$ が可分である必要十分条件は， $X$ が高々可算集合であることである。

稠密の例3でも述べた通り，離散空間では $\overline{A}=A$ なので， $X$ 自身以外に稠密な部分集合はありません。

ここから先は，関数解析でよく使う可分空間の例を挙げます。

可分の例5(連続写像の空間).

$C[0,1]=\{ f\colon [0,1]\to\R\mid f\text{ is continuous}\}$ を，連続写像 $f\colon [0,1]\to\R$ 全体の集合とする。この空間は，

\| f-g\|= \sup_{0\le x\le 1} |f(x)-g(x)|

により，バナッハ空間(よって距離空間，よって位相空間)と思える。この空間は可分である。

$\mathbb{Q}[x]$ を有理数係数多項式全体の集合とすると，これは可算集合であり， $C[0,1]$ の部分集合と見たときに， $C[0,1]$ の位相について $\overline{\mathbb{Q}[x]}=C[0,1]$ となります。これはワイエルシュトラスの多項式近似定理からわかります。よって，可分です。

可分の例6( $L^p$ 空間).

関数空間 $L^p(\R^n)$ は $1\le p<\infty$ のとき可分だが， $p=\infty$ のときは可分でない。

$1\le p<\infty$ のとき可分であることは，台(サポート)がコンパクトな連続関数の空間 $C_c(\R^n)$ が $L^p(\R^n)$ において稠密であることと，上の例6から従います。

可分の例7( $l^p$ 空間).

数列空間 $l^p$ は $1\le p<\infty$ のとき可分だが， $p=\infty$ のときは可分でない。

$1\le p<\infty$ のとき可分であることは，

l_{c,\mathbb{Q}}=\{ (a_1, \ldots, a_n, 0,\ldots)\mid a_i\in \mathbb{Q}, n\ge 1\}

が可算集合であることと，これが $l^p$ で稠密であることから分かります。

可分空間の性質

可分空間の重要な性質をいくつか紹介しておきましょう。

定理（可分空間の性質）

可分な位相空間の開集合は，部分空間として可分である
第二可算公理をみたす位相空間は可分である
可分な位相空間の連続写像による像は部分空間として可分である
距離空間においては，可分であること・第二可算であること・リンデレーフであることは同値である。
可分空間の高々連続体濃度の直積は可分である。

2.について，第二可算ならば可分は成立しますが，逆は成立しないことが知られています。ただし， $(X,\mathcal{O})$ が距離化可能ならば，4.の通り，同値になります。

1.と3.と5.のみ証明しましょう。

証明

1.について

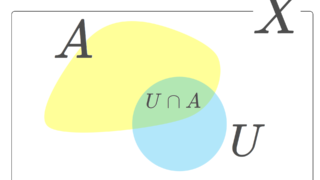
$D\subset X$ が $X$ において稠密であるとき， $D\cap A$ が $A$ において稠密であることを示す。

$B\subset A$ を $A$ における開集合とする。 $A$ は $X$ における開集合なので，相対位相と部分位相空間の定義・具体例5つ・性質5つの定理2.2より， $B$ も $X$ における開集合である。よって， $D\cap B \ne \emptyset$ であり，

D\cap B = D\cap (A\cap B)=(D\cap A)\cap B

なので， $(D\cap A)\cap B\ne\emptyset$ となる。ゆえに， $D\cap A$ は $A$ において稠密であることが示せた。 $D$ を可算集合と思うと， $D\cap A$ も高々可算集合なので，示せた。

3.について

$(X,\mathcal{O}_X), (Y, \mathcal{O}_Y)$ を位相空間， $f\colon X\to Y$ を連続とし， $X$ が可分であるとして， $f(X)$ も相対位相に関して可分であることを示す。

$X$ が可分なので，可算部分集合 $A\subset X$ で， $\overline{A}=X$ となるものが取れる。 $f$ は連続なので， $f(\overline{A})\subset \overline{f(A)}$ となる(→位相空間における連続写像の定義と性質を詳しく)。したがって， $f(X)\subset \overline{f(A)}$ となるので， $f(A)\subset f(X)$ は $f(X)$ において稠密である。 $f(A)$ は高々可算なので， $f(X)$ は可分である。

5.について

$\Lambda$ を高々連続体濃度とし，各 $\lambda\in \Lambda$ に対し， $X_\lambda$ を可分として，直積 $\prod_{\lambda\in\Lambda}X_\lambda$ が可分であることを示そう。 $\Lambda$ は高々連続体濃度なので， $\Lambda\subset [0,1]$ とみなせる。 $\{ x_{\lambda, n}\}_n\subset X_\lambda$ を可算な稠密部分集合とする。

$k\ge 1$ に対し， $J_1, J_2, \ldots, J_k \subset [0,1]$ を，端点が有理数である，どの2つも共通部分をもたない閉区間とする。さらに， $n_1, n_2, \ldots, n_k\ge 1$ とする。このとき， $p=p(J_1, \ldots, J_k; n_1, \ldots, n_k)\in X$ を

p_\lambda =\begin{cases} x_{\lambda, n_i} & \lambda\in J_i\cap\Lambda, \\ x_{\lambda, 1}& \text{otherwise} \end{cases}

と定める。ただし， $\pi_\lambda\colon X\ni p\mapsto p_\lambda \in X_\lambda$ は自然な射影である。 $k, J_1, \ldots, J_k, n_1, \ldots, n_k$ を動かして得られる $p(J_1, \ldots, J_k; n_1, \ldots, n_k)$ たち全体の集合を $P\subset X$ とすると， $P$ は明らかに可算である。これが稠密部分集合であることを示そう。 $X$ の開基は， $m\ge 1$ とし， $U_{\lambda_i}\subset X_{\lambda_i}$ を開集合とすることで，

U= \pi^{-1}_{\lambda_1} (U_{\lambda_1})\cap\cdots\cap \pi^{-1}_{\lambda_m} (U_{\lambda_m})

の形でかける。 $x_{\lambda_i, n_i} \in U_{\lambda_i}$ となる $n_i$ を取ってきて，さらに端点が有理数である，どの2つも共通部分をもたない閉区間 $J_1, J_2,\ldots, J_m$ を， $\lambda_i\in J_i$ となるようにとってくると， $p(J_1, \ldots, J_k; n_1, \ldots, n_k)\in U$ である。よって， $P$ が稠密であることが示された。

証明終

なお1.について，一般に可分な空間の部分空間が可分であるとは言えません。これについては，非可算集合 $X$ とある1点 $x\in X$ に対し，開集合系 $\mathcal{O}$ を

\mathcal{O}=\{\emptyset\}\cup \{ O\subset X \mid x\in O\}

で定めた位相空間 $(X, \mathcal{O})$ が良い例です。この位相は特定点位相 (particular point topology) といいます。この空間は， $\overline{\{x\}} =X$ なので可分ですが，部分空間 $X\setminus \{x\}$ は非可算な離散空間なので，可分ではありません。特定点位相は以下でも解説しています。