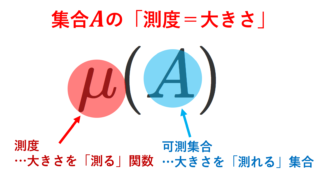
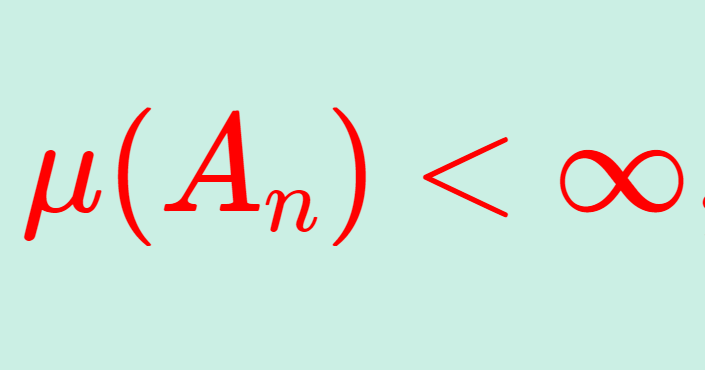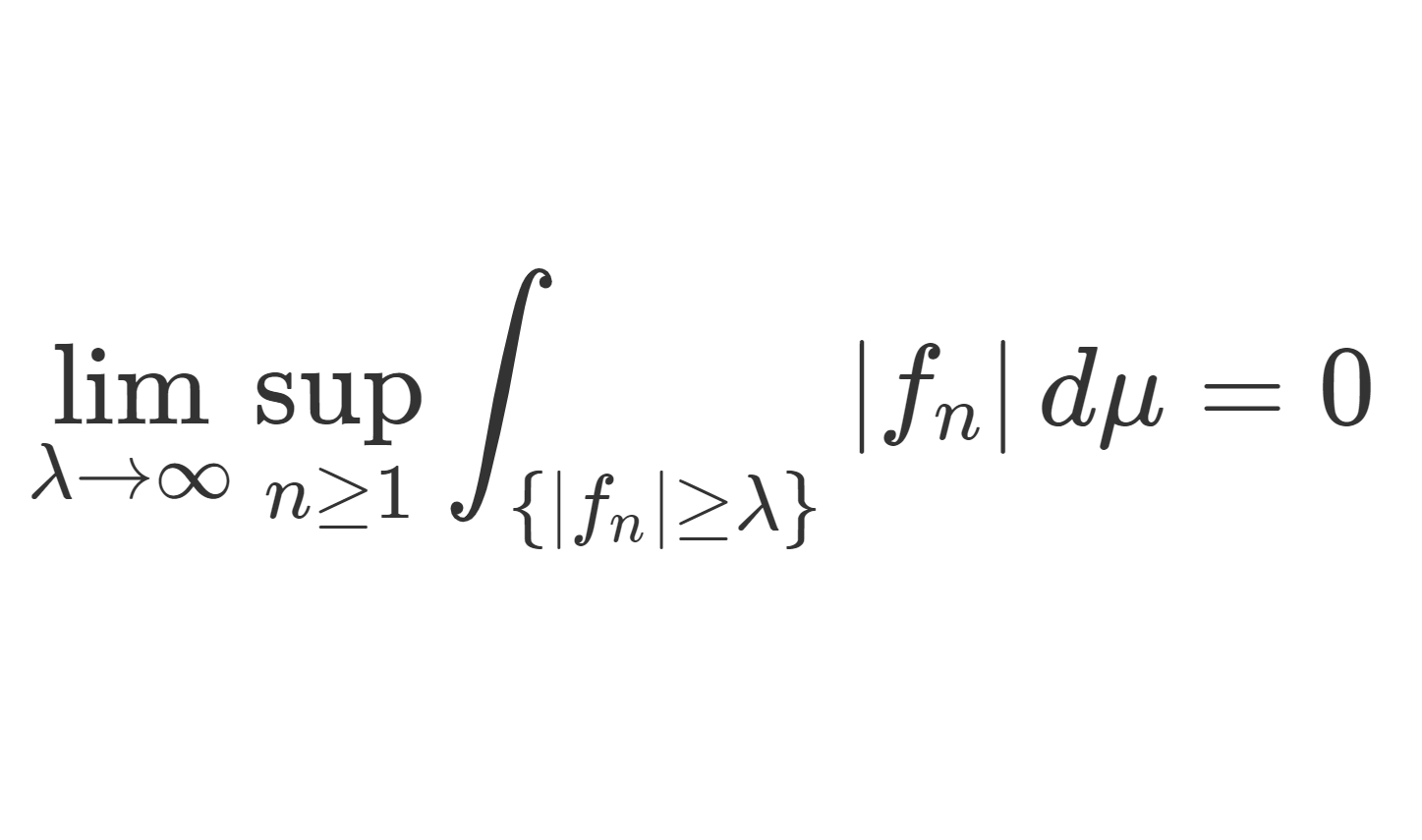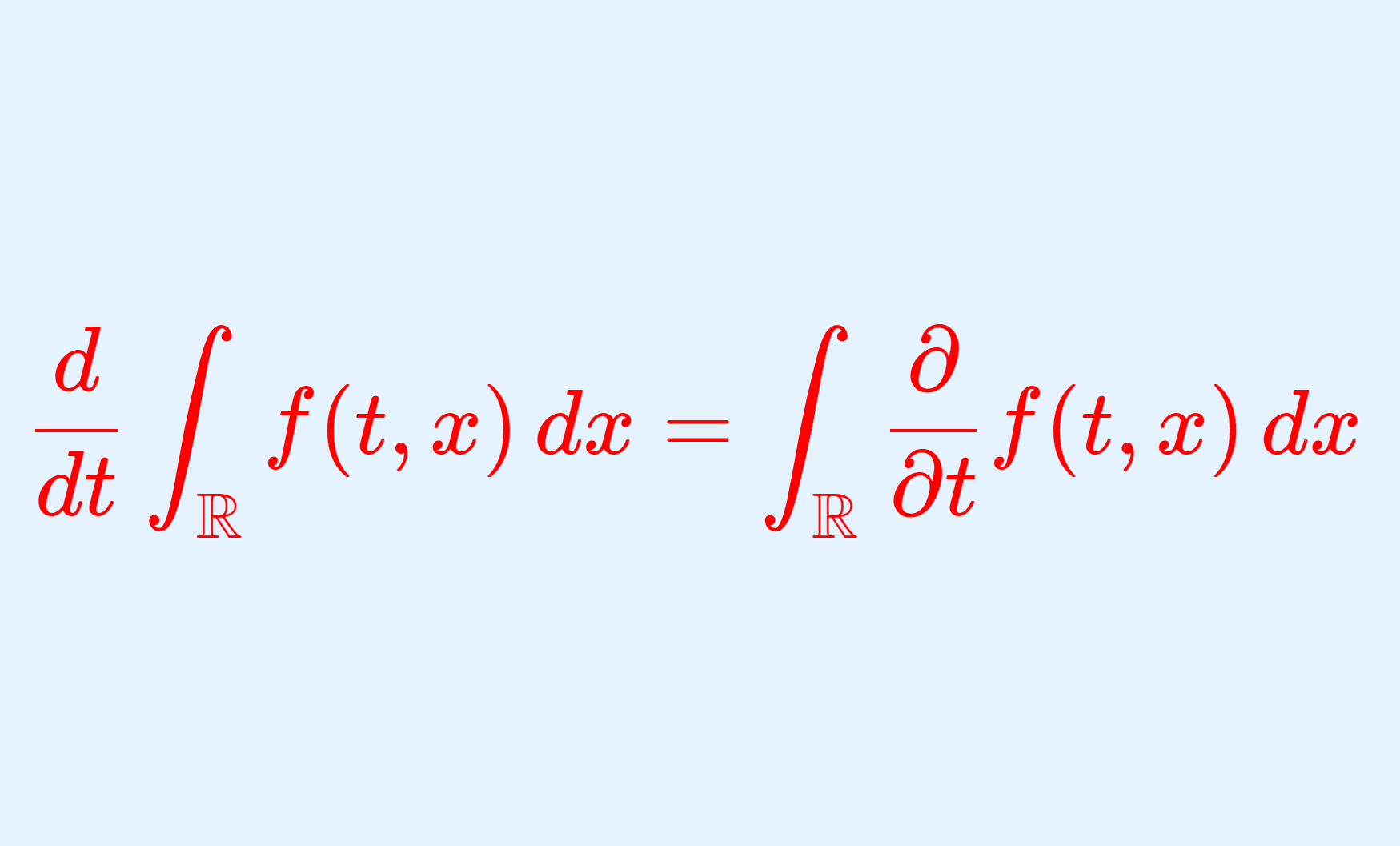σ-有限測度とは, \mu(A_n)<\infty \;(n\ge 1) かつ A_n\uparrow X となる可測集合列 \{A_n\} が取れることを言います。
σ-有限測度について,定義と具体例を挙げましょう。
σ-有限測度
以下で,集合について \color{red} A_n\uparrow X とは, A_1\subset A_2 \subset A_3\subset\cdots かつ X=\bigcup_{n=1}^\infty A_n となることを指します。
定義(σ-有限測度 ; \sigma\text{-finite})
(X,\mathcal{F}) を可測空間とし, \mu をその上の測度とする。
\mu がσ-有限 ( \sigma\text{-finite}) であるとは, A_n\uparrow X となる上昇列 \{A_n\}\subset\mathcal{F} が存在し,
\large \color{red}\mu(A_n)<\infty, \quad n\ge 1
となることをいう。
定義は上昇列ではなく,「 \{B_n\}\subset\mathcal{F} を X=\bigcup_{n=1}^\infty B_n かつ \mu(B_n)<\infty となるように取れる」ことと定義しても構いません。 A_n=\bigcup_{k=1}^n B_k とすれば,上の定義に帰着できますね。
注意ですが,σ-有限だからといって, \mu(X)<\infty (有限測度 (finite measure) という)とは限りません。
有限測度ならば必ずσ-有限ですが,逆は必ずしも成立しません。以下で例を挙げましょう。
σ-有限測度の具体例・反例
例1.
\mathbb{R}^d 上のルベーグ測度 \mathrm{Leb} はσ-有限だが有限測度でない。
まず, \mu(\mathbb{R}^d)=\infty なので,有限測度ではないですね。一方, [-n,n]^d とすると, [-n,n]^d\uparrow \mathbb{R}^d であり,
\mathrm{Leb}([-n,n]^d) = (2n)^d < \infty
となるため, \mathrm{Leb} はσ-有限測度ですね。
例2.
X 上の数え上げ測度(すなわち集合の要素の個数を返す測度)を \# とする。
- X が有限集合のとき,\# は有限測度である。
- X が可算集合のとき,\# は有限測度でないがσ-有限測度である。
それぞれ確認していきましょう。以下で \mathbb{N}=\{1,2,3,\ldots\} とします。
- X が有限測度なら, \#(X)<\infty ですから,有限測度ですね。
- X が可算集合なら, \#(X)=\infty より,有限測度ではありません。ここで,全単射 f\colon \mathbb{N}\to X をとり, A_n =f(\{1,2,\dots, n\})\subset X とおくと, A_n \uparrow X かつ \mu(A_n)=n<\infty ですから,σ-有限測度ですね。
例3.
(X,\mathcal{F},\mu) を測度空間, \mathcal{F}=\{\emptyset, X\}, \mu(X)=\infty とすると,これはσ-有限測度ではない。
このように,測度空間として「貧弱」の場合も,σ-有限測度にならないことがあります。