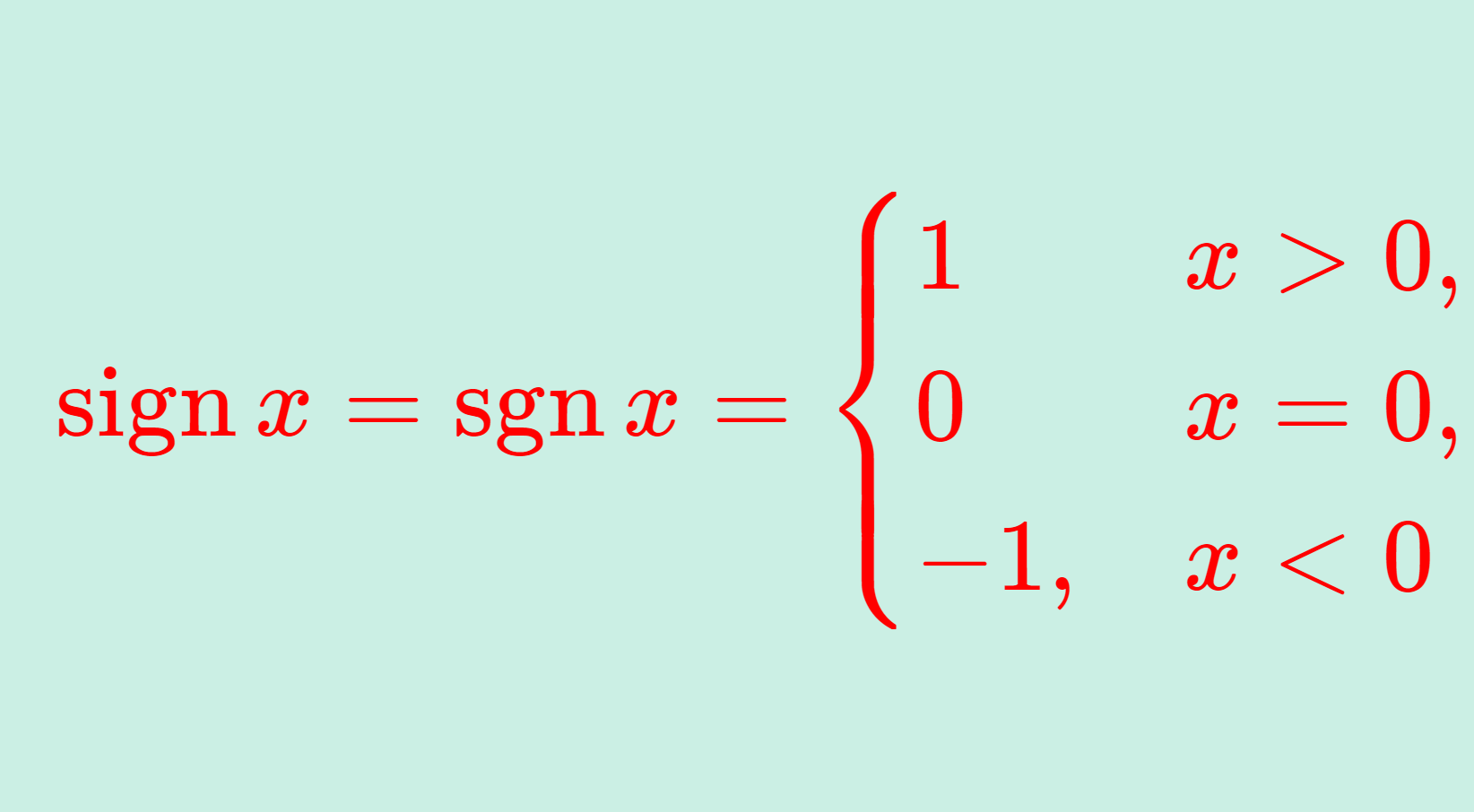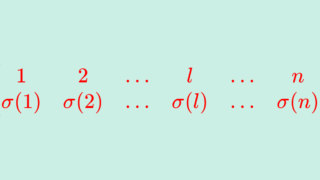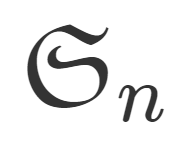sign関数(sgn関数,符号関数)とは何か

sign 関数，または sgn 関数とは，符号関数と言われ，定義は以下のようになります。

sign関数(sgn関数,符号関数)の定義

定義（符号関数）

\textcolor{red}{\operatorname{sign} x = \operatorname{sgn}\, x = \begin{cases} 1 & x > 0, \\ 0 & x = 0, \\ -1 & x< 0\\ \end{cases}}

と定義される関数 $\operatorname{sign}, \operatorname{sgn}\colon \mathbb{R} \to \{-1, 0, 1\}$ を符号関数 (sign function) という。

符号関数は，以下の性質があります。

Check～符号関数の性質～

群論や線形代数において登場する「置換」に対しても，この関数が使われることがあります。定義は以下のようになります。

定義（置換における符号関数）

$S_n$ を対称群， $\sigma \in S_n$ を置換とする。このとき，

\color{red} \operatorname{sign} \sigma = \operatorname{sgn} \sigma = \begin{cases} 1 & \sigma \text{ is even}, \\ -1 & \sigma \text{ is odd} \end{cases}

と定義される関数 $\operatorname{sign}, \operatorname{sgn}\colon S_n \to \{-1, 1\}$ を符号関数 (sign function) という。ただし，even, odd はそれぞれ偶置換・奇置換を表す。

これは群準同型になっていることが分かります。

対称群や置換・偶置換・奇置換については，たとえば以下の記事を参照してください。

注釈なしに出てくることもありますから，そういう時は参照してください。