ベクトル空間の和・直和の定義とその次元の等式の証明

ベクトル空間の和・直和についての定義と，次元に関する等式 $\dim (V+W) = \dim V + \dim W - \dim (V\cap W)$ の証明を行います。最後には，3つ以上の和・直和について考えます。

ベクトル空間の和・直和の定義
1. ベクトル空間の和の定義
2. ベクトル空間の直和の定義
和・直和の次元の等式とその証明
1. 定理の主張
2. 証明
3つ以上の和・直和とその性質
ベクトル空間に関する他の記事

ベクトル空間の和・直和の定義

まず，ベクトル空間の和・直和の定義を順に述べましょう。

ベクトル空間の和の定義

定義（ベクトル空間の和）

$V$ をベクトル空間， $V_1 , V_2 \subset V$ を部分ベクトル空間とする。このとき， $V_1, V_2$ の和 (sum) $\color{red} V_1 + V_2$ とは

\color{red} V_1 + V_2 = \{\boldsymbol{v_1} + \boldsymbol{v_2} \mid \boldsymbol{v_1} \in V_1, \boldsymbol{v_2} \in V_2 \}

のことを言う。

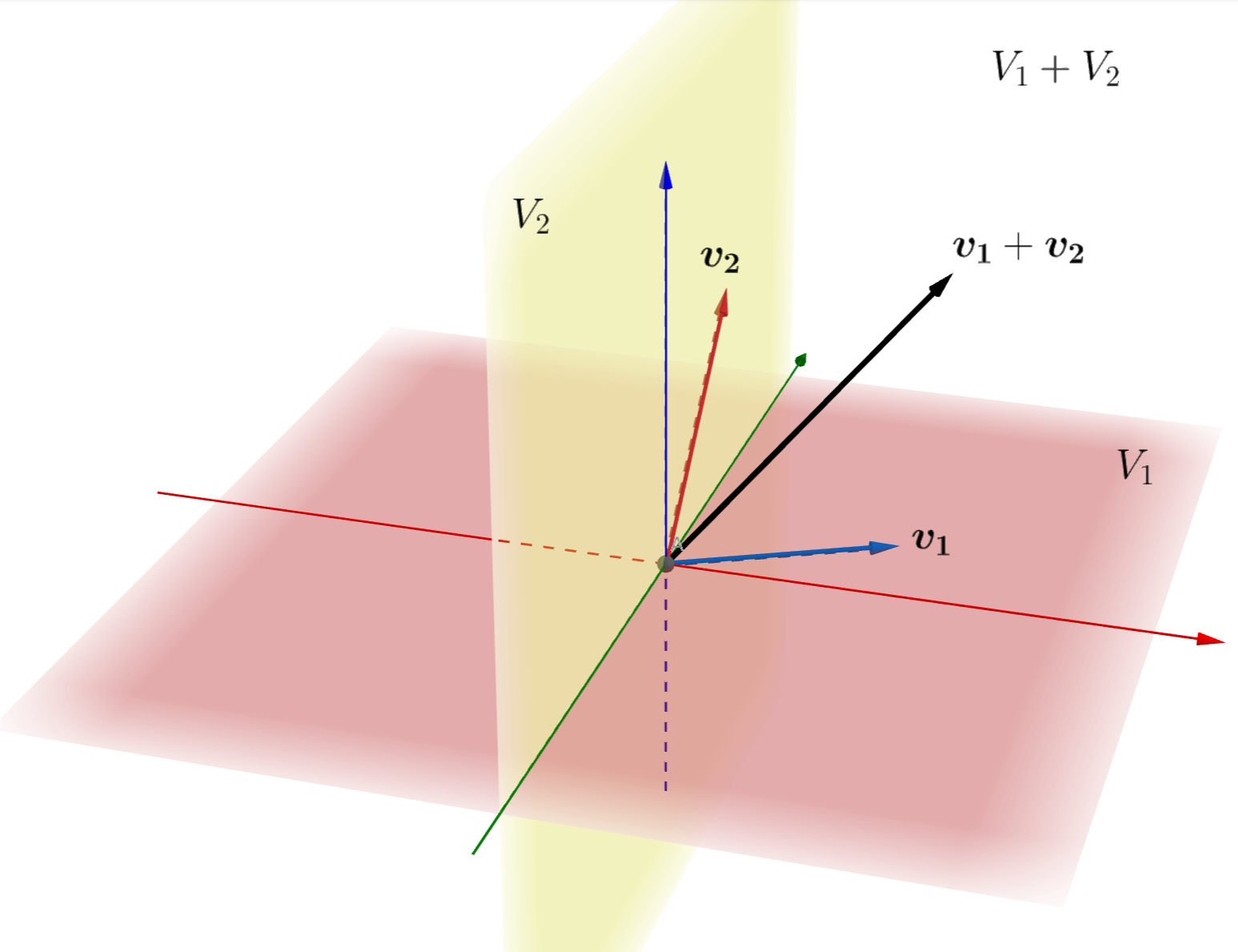
なお， $V_1 + V_2$ は $V_1 \cup V_2$ を含む最小の部分ベクトル空間になっています( $V_1 \cup V_2$ はベクトル空間でないことに注意)。この空間を和空間とも言います。

図にすると，以下のようなイメージです。

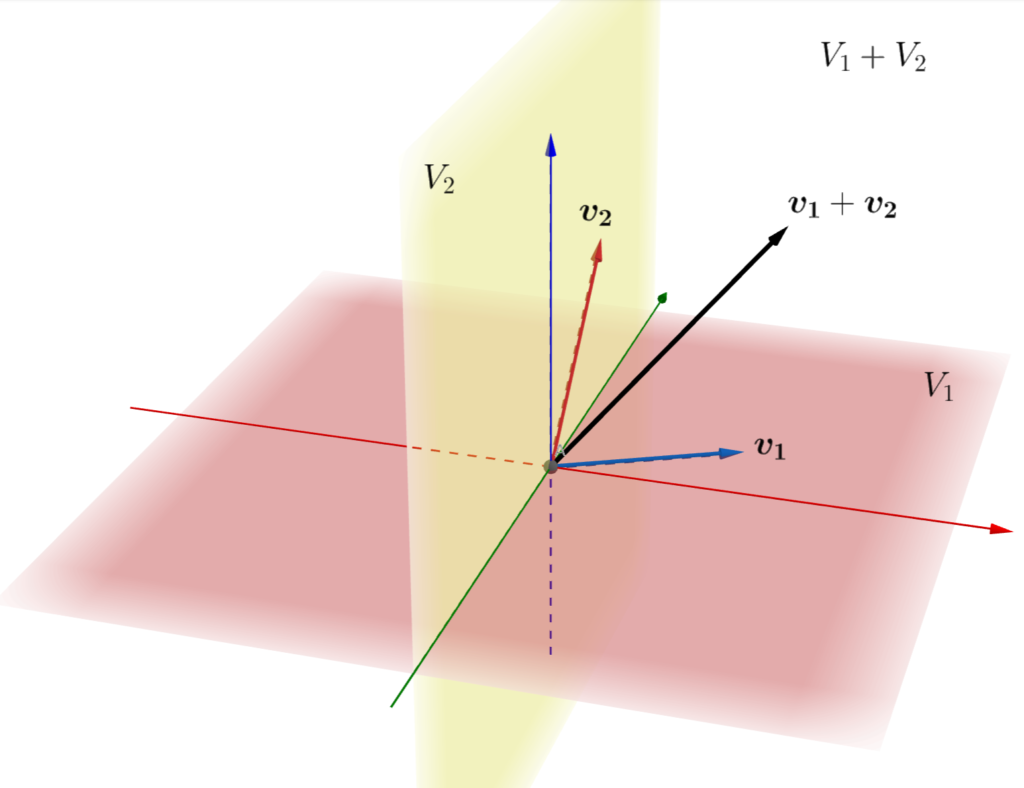
ベクトル空間の直和の定義

定義（ベクトル空間の直和）

和の定義において， $\color{red} V_1 \cap V_2 = \{\boldsymbol{0}\}$ となるとき， $V_1 + V_2$ を $V_1 , V_2$ の直和 (direct sum) または直和空間といい，しばしば $\color{red} V_1 \oplus V_2$ とかく。

「ダブりのない」2つの空間の和を直和というんですね。

なお，直和の定義は以下と同値です。

定理（ベクトル空間の直和）

$V^\prime= V_1 \oplus V_2$ となる必要十分条件は

任意の $\boldsymbol{v} \in V^\prime$ に対して，ただ一つ $\boldsymbol{v_1} \in V_1, \boldsymbol{v_2} \in V_2$ が存在して， $\boldsymbol{v} = \boldsymbol{v_1} + \boldsymbol{v_2}$ と書ける

ことである。

実際， $\impliedby$ (必要性)は和の定義から明らかで，
$\implies$ (十分姓)については，もし $\boldsymbol{v_1} + \boldsymbol{v_2} = \boldsymbol{v^\prime_1} + \boldsymbol{v^\prime_2} \,\, (\boldsymbol{v_1}, \boldsymbol{v^\prime_1} \in V_1, \boldsymbol{v_2}, \boldsymbol{v^\prime_2} \in V_2)$ とすると， $\boldsymbol{v_1} - \boldsymbol{v^\prime_1} = \boldsymbol{v^\prime_2} - \boldsymbol{v_2}$ なので，両辺 $V_1 \cap V_2 = \{\boldsymbol{0}\}$ に属することから， $\boldsymbol{v_1} = \boldsymbol{v^\prime_1}, \boldsymbol{v_2} = \boldsymbol{v^\prime_2}$ が直ちに従います。

和・直和の次元の等式とその証明

和・直和の次元について，以下のような等式が成立します。

定理の主張

定理（次元の等式）

$V$ をベクトル空間， $V_1 , V_2 \subset V$ を有限次元部分ベクトル空間とする。このとき，

\color{red} \begin{aligned} &\dim (V_1+V_2) \\ &= \dim V_1 + \dim V_2 - \dim (V_1 \cap V_2) \end{aligned}

である。特に，

\color{red} \dim (V_1 \oplus V_2) = \dim V_1 + \dim V_2

となる。

$V_1 \cap V_2$ も部分ベクトル空間であることに注意してください。

証明

早速証明しましょう。「特に」以下は前半が出れば $\dim \{\boldsymbol{0}\} =0$ からわかるので，前半を示します。

証明には基底の知識が必要です(→ベクトル空間の基底と次元～定義と具体例5つ～)。

証明

$d = \dim (V_1 \cap V_2 )$ とし， $V_1 \cap V_2$ の基底を $\{ \boldsymbol{v_1}, \boldsymbol{v_2}, \dots, \boldsymbol{v_d}\}$ とする。

$V_1 \cap V_2 \subset V_1$ より，この基底を延長する形で $V_1$ の基底を $\{ \boldsymbol{v_1}, \boldsymbol{v_2}, \dots, \boldsymbol{v_d}, \boldsymbol{v^1_1}, \boldsymbol{v^1_2}, \dots, \boldsymbol{v^1_{r_1}}\}$ とできる(→部分ベクトル空間の基底の延長により全体空間の基底が取れる証明)。ただし， $d + r_1 = \dim V_1$ である。
同様に， $V_1 \cap V_2$ の上の基底を延長することで， $V_2$ の基底 $\{ \boldsymbol{v_1}, \boldsymbol{v_2}, \dots, \boldsymbol{v_d}, \boldsymbol{v^2_1}, \boldsymbol{v^2_2}, \dots, \boldsymbol{v^2_{r_2}}\}$ とできる。ただし， $d + r_2 = \dim V_2$ である。

さて， $V_1 + V_2$ の基底を $\{ \boldsymbol{v_1}, \dots, \boldsymbol{v_d}, \boldsymbol{v^1_1}, \dots, \boldsymbol{v^1_{r_1}} ,\boldsymbol{v^2_1}, \dots, \boldsymbol{v^2_{r_2}}\}$ とできることを示そう。
$V_1 + V_2$ の任意の元は $\boldsymbol{v_1} + \boldsymbol{v_2}, \,\, \boldsymbol{v_1} \in V_1, \boldsymbol{v_2} \in V_2$ と表せ， $\boldsymbol{v_1}, \boldsymbol{v_2}$ はそれぞれ $V_1 , V_2$ の基底の一次結合で表せるから， $V_1 + V_2$ の任意の元は $\{ \boldsymbol{v_1}, \dots, \boldsymbol{v_d}, \boldsymbol{v^1_1} , \dots, \boldsymbol{v^1_{r_1}} ,\boldsymbol{v^2_1}, \dots, \boldsymbol{v^2_{r_2}}\}$ の一次結合で書ける。
よって残り示すべきなのは，上が一次独立であることである。そこで，

\begin{aligned} &k_1\boldsymbol{v_1}+ \dots + k_d \boldsymbol{v_d} \\ &+ l^1_1\boldsymbol{v^1_1}+ \dots + l^1_{r_1} \boldsymbol{v^1_{r_1}} \\ &+ l^2_1\boldsymbol{v^2_1}+ \dots + l^2_{r_2}\boldsymbol{v^2_{r_2}} = \boldsymbol{0} \end{aligned}

としよう。式変形して，

\begin{aligned}\tag{1} &k_1\boldsymbol{v_1}+ \dots + k_d \boldsymbol{v_d} \\ &+ l^1_1\boldsymbol{v^1_1}+ \dots + l^1_{r_1} \boldsymbol{v^1_{r_1}} \\ &= -l^2_1\boldsymbol{v^2_1}- \dots -l^2_{r_2}\boldsymbol{v^2_{r_2}} \end{aligned}

である。左辺は $V_1$ に属し，右辺は $V_2$ に属するから，両辺 $V_1 \cap V_2$ に属する。すると，特に右辺は $V_1 \cap V_2$ の基底で書ける。すなわち，

\begin{aligned} &-l^2_1\boldsymbol{v^2_1}- \dots -l^2_{r_2}\boldsymbol{v^2_{r_2}} \\ &= k^\prime_1\boldsymbol{v_1}+ \dots + k^\prime_d \boldsymbol{v_d} \end{aligned}

とできる。一方で $\{ \boldsymbol{v_1}, \boldsymbol{v_2}, \dots, \boldsymbol{v_d}, \boldsymbol{v^2_1}, \boldsymbol{v^2_2}, \dots, \boldsymbol{v^2_{r_2}}\}$ は $V_2$ の基底なので，

l^2_1 = \dots = l^2_{r_2} = k^\prime_1 = \dots =k^\prime_d = 0.

である。これを $(1)$ 式に入れて，

\begin{aligned} &k_1\boldsymbol{v_1}+ \dots + k_d \boldsymbol{v_d} \\ &+ l^1_1\boldsymbol{v^1_1}+ \dots + l^1_{r_1} \boldsymbol{v^1_{r_1}} \\ &= \boldsymbol{0} \end{aligned}

となる。上記は $V_1$ の基底の一次結合なので，

k_1 = \dots = k_d = l^1_1 = \dots l^1_{r_1} = 0 .

これより， $\{ \boldsymbol{v_1}, \dots, \boldsymbol{v_d}, \boldsymbol{v^1_1} , \dots, \boldsymbol{v^1_{r_1}} ,\boldsymbol{v^2_1}, \dots, \boldsymbol{v^2_{r_2}}\}$ は一次独立であることもわかる。

以上から， $\dim(V_1+V_2) = d + r_1 + r_2 = \dim V_1 + \dim V_2 - \dim (V_1 \cap V_2 ) .$

証明終