階乗の一般化であり,解析学でよく使われるガンマ関数は, \operatorname{Re} z>0 に対し, \Gamma(z) = \int_0^\infty t^{z-1}e^{-t}\, dt と定義される関数です。これについて,その定義と性質を詳しく述べましょう。
ガンマ関数の定義
今回はガンマ関数を,複素数 \operatorname{Re}z>0 で定義しますが,複素関数が分からない場合は,単に z>0 (正の実数)と思えばよいです。
定義(ガンマ関数)
\operatorname{Re} z>0 に対し,
\large \color{red} \Gamma(z) = \int_0^\infty t^{z-1}e^{-t}\, dt
をガンマ関数 (gamma function) という。
ガンマ関数の積分が収束していることについて考えましょう。 |t^z| = |e^{z\log t}| = e^{\operatorname{Re}( z) \log t} = t^{\operatorname{Re} z} に注意すると,
\begin{aligned}&\int_0^\infty |t^{z-1}e^{-t}| \, dt= \int_0^\infty t^{\operatorname{Re} (z) -1} e^{-t} \, dt \\ &\le \int_0^1 t^{\operatorname{Re} (z) -1}\, dt + \int_1^\infty t^n e^{-t}\, dt \end{aligned}
ただし, n \ge \operatorname{Re} z - 1 であり, \operatorname{Re}z > 0 より右辺の2つの広義積分は収束するため,
となって,ガンマ関数の積分がちゃんと収束していることがわかりますね。
ガンマ関数を,実数の範囲に限った \Gamma(x)\; (x>0) のグラフを描くと,以下のようになります。
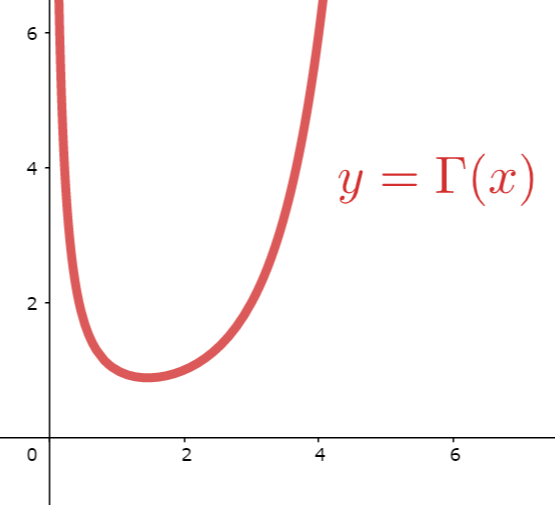
ガンマ関数の性質
ガンマ関数の性質について述べましょう。
ガンマ関数は階乗の一般化である
定理(ガンマ関数と階乗)
\operatorname{Re} z>0 とすると, \color{red} \Gamma(z+1) =z\Gamma(z) である。
また, \Gamma(1) = 1 であるから,正の整数 n \ge 1 に対し, \color{red} \Gamma(n) = (n-1)! である。
証明は,複素関数論が分からなくても理解できると思います。確認していきましょう。
証明
部分積分により,
\begin{aligned} \Gamma(z+1) &=\int_0^\infty t^z (-e^{-t})' \, dt \\ &= \left[ -t^z e^{-t}\right]_0^\infty + z \int_0^\infty t^{z-1} e^{-t}\, dt \\ &= z\Gamma(z) \end{aligned}
より,前半は示せた。また,
であり,このことから, n \ge 1 を正の整数として,
を得る。
証明終
なお, \Gamma(z+1) = z\Gamma(z) から,\color{red} \Gamma(z) = \dfrac{\Gamma(z+1)}{z} ですが,これを -1< \operatorname{Re} z \le 0,\; z\ne 0 に適用することで, \Gamma(z) は \operatorname{Re} >-1, \;z\ne 0 の範囲に拡張(解析接続)することが可能です。
同様に,何度も \Gamma(z) = \dfrac{\Gamma(z+1)}{z} を適用することで,結局, \Gamma(z) は z\ne 0,-1,-2,-3,\ldots をみたす全ての複素数に拡張(解析接続)できます。(厳密には,そもそもガンマ関数が \operatorname{Re} z>0 上正則(解析的)ということが言えないと,「拡張できる」というのは意味不明ですが,その証明は下の方でしていますので解析学の知識があれば適宜参照してください。)
拡張したときの \Gamma(x)\;(x \in \mathbb{R}\setminus\{ 0,-1,-2,-3,\ldots\}) のグラフは以下のようになります。
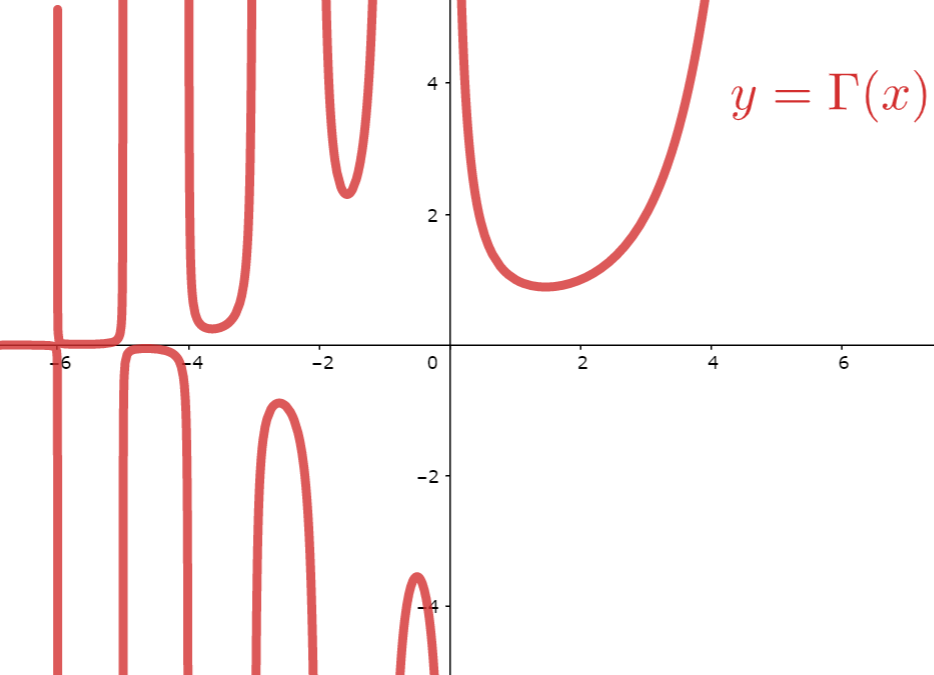
Γ(1/2)の値
定理( \Gamma(1/2) の値)
\color{red} \Gamma\left(\frac{1}{2}\right) = \sqrt{\pi}
である。
\Gamma(1/2) の計算はガウス積分に帰着されます。証明を紹介しましょう。
証明
u = t^{1/2} とおいて置換積分すると,
\begin{aligned}\Gamma\left(\frac{1}{2}\right) &= \int_0^\infty t^{-1/2} e^{-t}\, dt \\ &= \int_0^\infty u^{-1} e^{-u^2}\, 2udu \\ &= 2\int_0^\infty e^{-u^2} \, du \\ &= \sqrt{\pi} \end{aligned}
ただし,最後の等式はガウス積分の公式を用いた(→ガウス積分のさまざまな形とその証明5つ)。
証明終
なお,この定理と \Gamma(z+1) =z\Gamma(z) から, \Gamma(1/2+n) \; (n\in \mathbb{Z} ) は求まることになります。たとえば,
\begin{aligned} \Gamma\left(-\frac{1}{2}\right) &= -2\sqrt{\pi}, \\ \Gamma\left(\frac{3}{2}\right) &= \frac{\sqrt{\pi}}{2}\end{aligned}
となります。
ガンマ関数は正則(解析的)である
ガンマ関数が \operatorname{Re} z>0 上正則関数であることを示しましょう。ここからは,解析学の知識が必要です。
定理(ガンマ関数の正則性)
\Gamma(z) は \operatorname{Re} z > 0 上正則である。
じゃっかん略証気味ですが,いきましょう。
証明
\alpha = \operatorname{Re} z> 0 とし, h \in \mathbb{C} を |h| < \alpha / 2 とする。このとき, e^{\alpha/2}\le |e^{z+h}|\le e^{3\alpha/2} に注意する。
\frac{\Gamma(z+h)-\Gamma(z)}{h} = \int_0^\infty \frac{t^{z+h-1}-t^{z-1}}{h}e^{-t}\, dt.
ここで,積分の中身について,
であり,最後の積分は (0,\infty) 上可積分であるから,ルベーグの収束定理より, h\to 0 とすることで, \Gamma(z) は可微分である。よって, \Gamma(z) は \operatorname{Re} z>0 上正則である。
証明終
なお実際は,ガンマ関数は,前述した方法で非正の整数 0,-1,-2,\ldots で 1 位の極を持つ \mathbb{C} 上の有理型関数に解析接続できます。
その他の性質
証明はしませんが,他の性質をいくつか挙げておきましょう。
定理(ガンマ関数のその他の性質)
- \displaystyle \Gamma(z) = \frac{1}{z} \prod_{n=1}^\infty \frac{(1+\frac{1}{n})^z}{1+\frac{z}{n}},\;\; z\in\mathbb{C}\setminus\{0,-1,-2,\ldots\}.
- \displaystyle \Gamma(z)\Gamma(1-z) =\frac{\pi}{\sin \pi z}, \; \;z\in \mathbb{C}\setminus\mathbb{Z}. (相反公式; Euler’s reflection furmula)