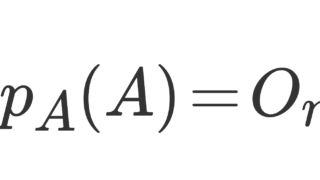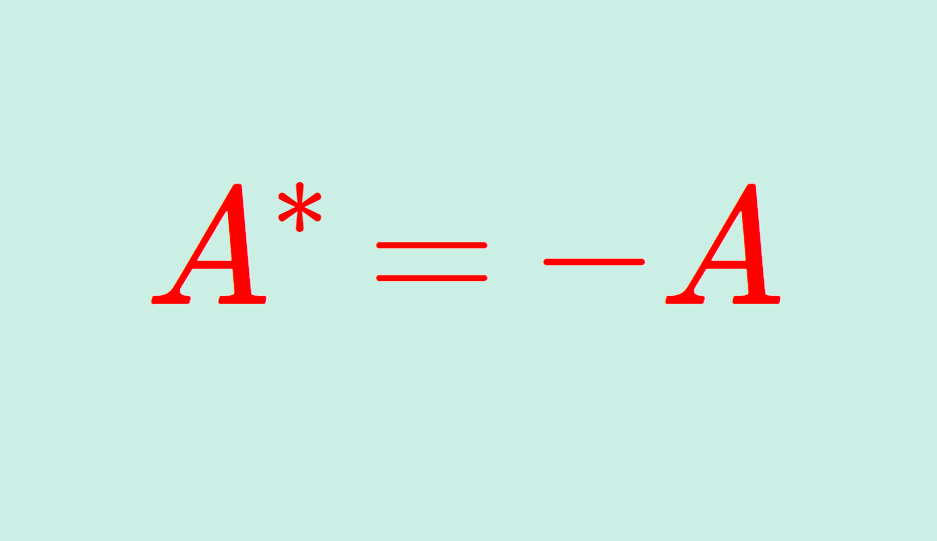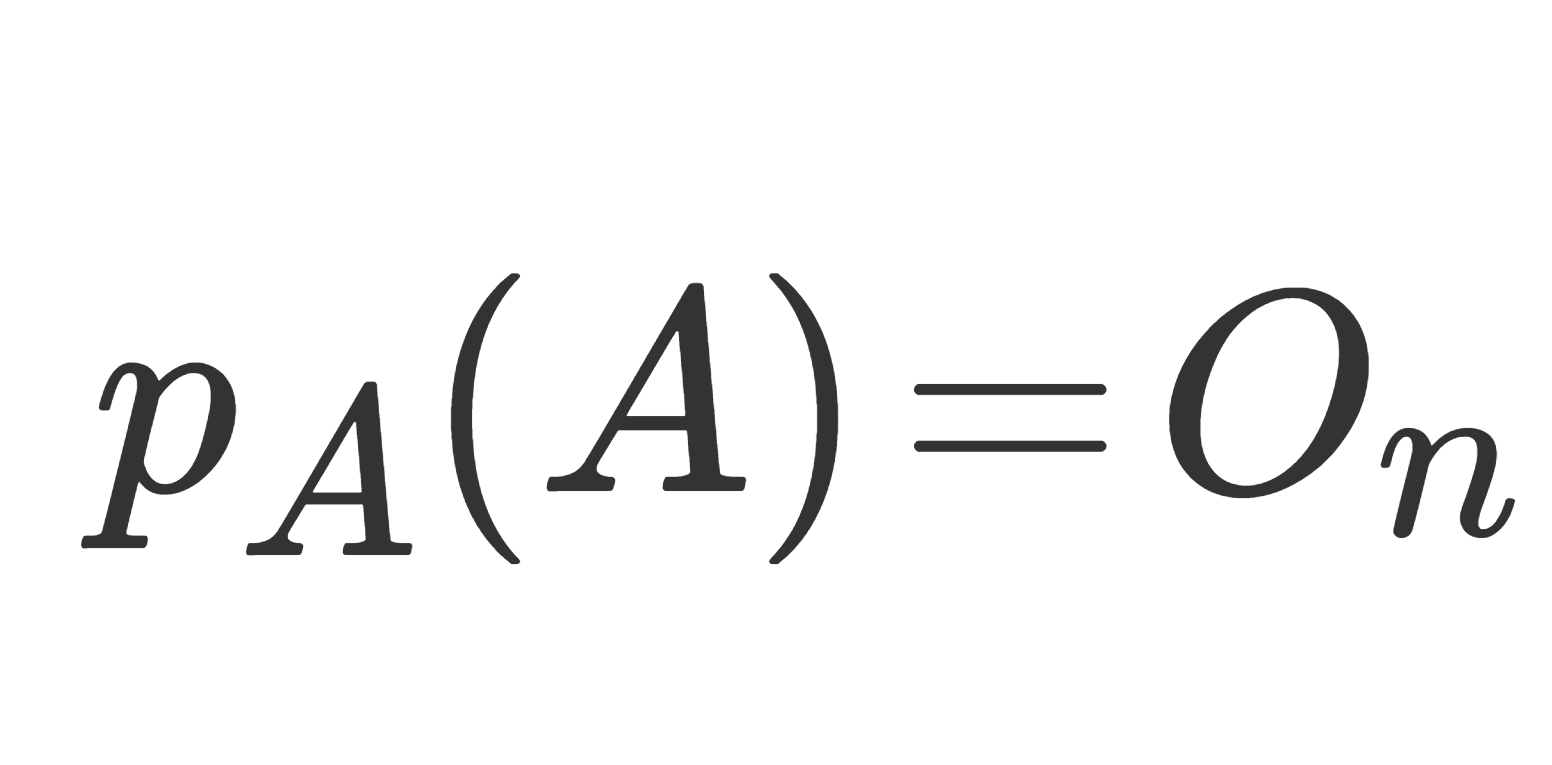固有値に関するフロベニウスの定理とその証明

行列の固有値における，フロベニウスの定理を紹介し，証明をていねいに行いましょう。

フロベニウスの定理
フロベニウスの定理の証明の準備
フロベニウスの定理の証明
関連する記事

フロベニウスの定理

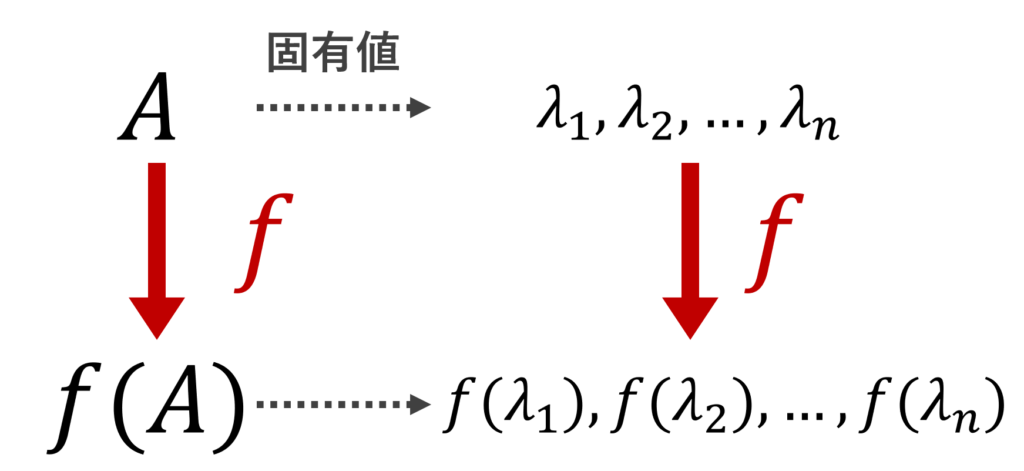
フロベニウスの定理 (Frobenius theorem)

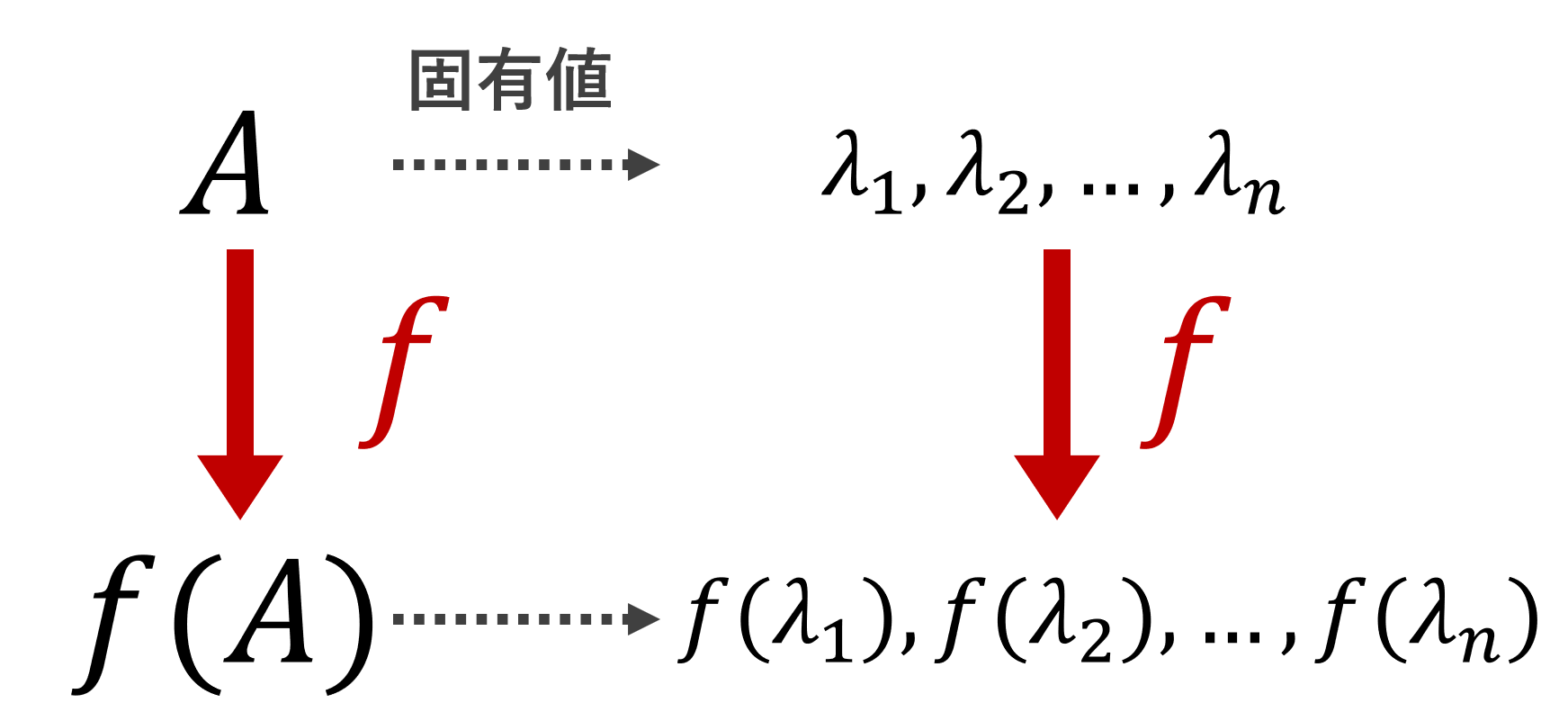
$f(x) =a_mx^m+a_{m-1}x^{m-1}+\dots +a_0$ を多項式とする。 $n$ 次正方行列 $A$ の固有値を $\lambda_1,\lambda_2,\dots, \lambda_n$ とするとき，正方行列

f(A)= a_mA^m+a_{m-1}A^{m-1}+\dots +a_0 I_n

の固有値は $f(\lambda_1),f(\lambda_2), \dots, f(\lambda_n)$ である。

行列を多項式に突っ込むと，固有値もそれに対応して多項式に突っ込んだものになる，という定理ですね。

ここで固有値 $\lambda_1,\lambda_2,\dots, \lambda_n$ は重複があって構いません。

フロベニウスの定理の証明の準備

証明には以下の4つの知識が必要です。

$f(P^{-1}AP)=P^{-1}AP$ であること
正方行列は三角化可能であること
相似な行列の固有値は同じであること
三角行列の固有値・三角行列同士の和と積の性質

順番に確認していきましょう。

1. f(P^{-1}AP)=P^{-1}f(A)P であること

補題 ( $A,B$ が相似なら $f(A),f(B)$ も相似である)

$f$ を多項式とする。 $A$ を正方行列， $P$ を正則行列(可逆行列)とするとき， $\color{red} f(P^{-1}AP)=P^{-1}f(A)P$ が成立する。特に， $A,B$ が相似ならば， $f(A),f(B)$ も相似である。

$A,B$ が相似とは，ある正則行列(可逆行列) $P$ が存在して， $B=P^{-1}AP$ とできることを指します(→行列の相似とは～定義と性質6つの証明～)。

証明

以下， $A,B$ を正方行列， $c$ を定数， $P$ を正則行列(可逆行列)とする。

行列の和について，分配法則より， $P^{-1}AP+P^{-1}BP=(P^{-1}A+P^{-1}B)P=P^{-1}(A+B)P$ が成立する。
行列の定数倍について， $c(P^{-1}AP)=P^{-1}(cA)P$ が成立する。
行列の積について， $(P^{-1}AP)^k = P^{-1}A(PP^{-1})A(PP^{-1})\cdots AP = P^{-1}A^kP$ が成立する。

以上の3つを3.→2.→1.の順に用いることにより， $f(P^{-1}AP)=P^{-1}f(A)P$ がわかる。

証明終

2. 正方行列は三角化可能であること

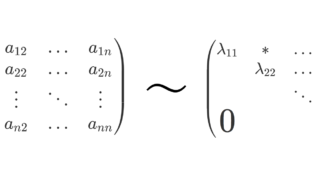
任意の正方行列 $A$ は，上三角行列と相似です。すなわち，ある正則行列(可逆行列) $P$ が存在して， $T=P^{-1}AP$ を上三角行列とすることができます。上三角行列とは

T= \begin{pmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ & a_{22} &\dots & a_{2n} \\ &&\ddots & \vdots \\ \huge{0}&&&a_{nn} \end{pmatrix}

のような形のことです。この定理については，以下で証明しています。

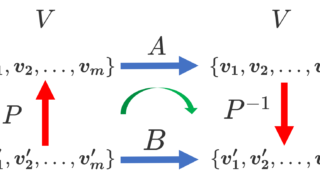
3. 相似な行列の固有値は同じであること

$A,B$ が相似であるとしたとき， $A,B$ の固有値は同じになります。これは以下の中で解説しています。

4. 三角行列の対角成分は固有値・三角行列同士の和,積の性質

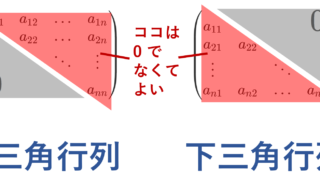
上三角行列の対角成分は固有値になります。

また，上三角行列同士の和は再び上三角行列になり，積も再び上三角行列になります。特に積については，

\begin{aligned}A&= \begin{pmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ & a_{22} &\dots & a_{2n} \\ &&\ddots & \vdots \\ \huge{0}&&&a_{nn} \end{pmatrix} ,\\ B&= \begin{pmatrix} b_{11} & b_{12} & \dots & b_{1n} \\ & b_{22} &\dots & b_{2n} \\ &&\ddots & \vdots \\ \huge{0}&&&b_{nn} \end{pmatrix} \end{aligned}

に対し，

AB= \begin{pmatrix} a_{11}b_{11} & \ast & \dots & \ast \\ & a_{22}b_{22}&\dots & \ast \\ &&\ddots & \vdots \\ \huge{0}&&&a_{nn}b_{nn} \end{pmatrix}

の形になります。対角成分は単に同じ場所の成分をかけ算しただけであることが大切です。

これらについては，以下で述べています。

フロベニウスの定理の証明

以上の知識を用いて，フロベニウスの定理の証明をしていきましょう。

証明

正方行列 $A$ は上三角行列と相似である(知識2.)から，正則行列(可逆行列) $P$ を用いて $T=P^{-1}AP$ が上三角行列としてよい。知識1.より，

P^{-1}f(A) P=f(P^{-1}AP)=f(T).

知識4.より， $f(T)$ は上三角行列で，その対角成分は $f(\lambda_1),f(\lambda_2),\dots, f(\lambda_n)$ であるから， $f(T)=P^{-1}f(A)P$ の固有値が $f(\lambda_1),f(\lambda_2),\dots, f(\lambda_n)$ である。

固有値は相似変換しても変わらない(知識3.)から， $f(A)$ の固有値は $f(\lambda_1),f(\lambda_2),\dots, f(\lambda_n)$ である。

証明終

無事に証明できましたね。このように，相似変換して性質の良い行列にしてから扱うという手法は非常に便利です。