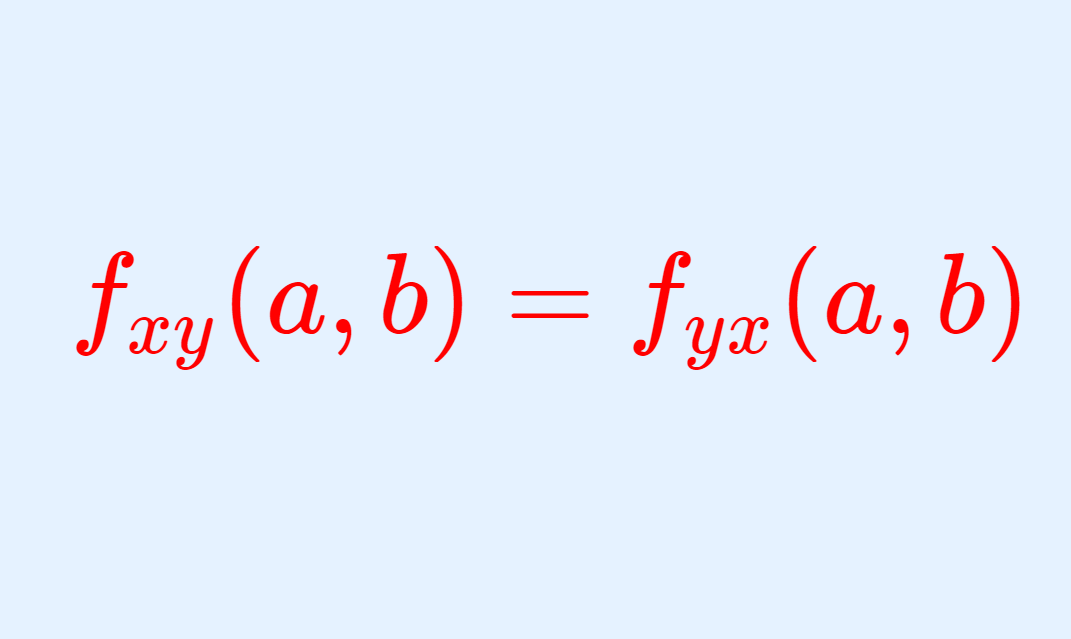高階偏微分においては,「偏微分する順番は多くの場合,気にしなくて良い」という定理があります。シュワルツの定理と呼ばれる本定理を紹介し,それを証明したいと思います。
最後には,シュワルツの定理が適用できない例(偏微分の順序交換ができない例)も述べます。
本記事は偏微分を既知とします。これについては,偏微分とは~定義と例題と図形的意味~を参照してください。
【fxy=fyx】シュワルツの定理
以下,特に言及しない限り, A\subset \mathbb{R}^2 を2次元の領域とし, f\colon A\to \mathbb{R} を2変数実数関数とします。
定理(シュワルツの定理)
2変数関数 f(x,y) は (a,b)\in A の近くで f_y, f_{xy} が存在するとし, f_{xy} は (a,b) で連続とする。
このとき, f_{yx}(a,b) も存在して,
が成立する。
多くの場合において,偏微分する順番は気にしなくて良いと言っている定理です。
これを用いると,以下のようなことが直ちに従います。
系(偏微分の順序交換)
- 偏導関数 f_{xy},f_y が存在して, f_{xy} が連続ならば,偏導関数 f_{yx} も存在して, f_{xy}=f_{yx} である。
- 偏導関数 f_{xy},f_{yx} が存在して,少なくとも一方が連続ならば, f_{xy}=f_{yx} である。
- f が C^2 級であれば, f_{xy} = f_{yx} である。
- f が C^n 級であるならば, k 階偏導関数 (0\le k \le n ) は全て
\frac{\partial^k f}{\partial x^r \partial y^{k-r}} \quad (0\le r\le k) の形でかける。
f が C^n 級であるとは, f が n 階までのあらゆる偏導関数をもち,それらがすべて連続であることを指します(→C1級,Cn級,C∞級関数の定義と具体例5つ)。
4.は非常に便利ですね。さらに, C^n 級の m 変数関数 f\colon \mathbb{R}^m\to \mathbb{R} における偏微分も,
\frac{\partial^{n_1+n_2+\dots +n_m} f}{\partial x_1^{n_1} \partial x_2^{n_2} \dots \partial x_m^{n_m} } \quad (n_1+n_2+\dots +n_m \le n)
の形でかけます。
シュワルツの定理の証明
シュワルツの定理を証明しましょう。
証明
\varphi(x,y)=f(x,y)-f(x,b) とおく。絶対値が十分小さい h,k をとると, x に関する平均値の定理より,
\begin{aligned}&\varphi(a+h,b+k) - \varphi(a,b+k)\\ &= h\varphi_x (a+\theta_k h, b+k) \\ &= h\{ f_x(a+\theta_k h, b+k)-f_x(a+\theta_k h, b)\} \end{aligned}\tag{1}
となる 0\le\theta_k\le 1 が存在する。さらに, y に関する平均値の定理より,
となる 0\le\theta'_{h,k}\le 1 が存在する。 ここで,
であり,これと (1),(2) 式より,
である。 f_{xy} は (a,b) で連続なので,両辺 h\to 0 として,
証明終
偏微分の順序交換ができない例
上では,偏微分の順序交換ができる十分条件を考えましたが,逆に順序交換ができない例を見ておきましょう。以下は有名な例です。
偏微分の順序交換ができない例
f(x,y)=\begin{dcases}\frac{xy(x^2-y^2)}{x^2+y^2} &(x,y)\ne (0,0), \\ 0 & (x,y) = (0,0)\end{dcases}
は, f_{xy}(0,0) = 0\ne 1 = f_{yx}(0,0) となる。
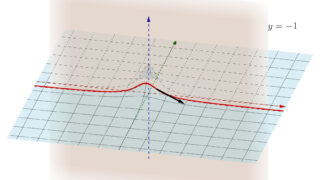
より, f_{xy}(0,y)=-1 ですが,
なので, f_{yx}(0,x) = 1 となって, f_{xy}(0,0) = 0\ne 1 = f_{yx}(0,0) ですね。
上の計算では出てきませんが, f_{xy} は (0,0) で連続にならないことが計算により確認できるため,シュワルツの定理は使えません。