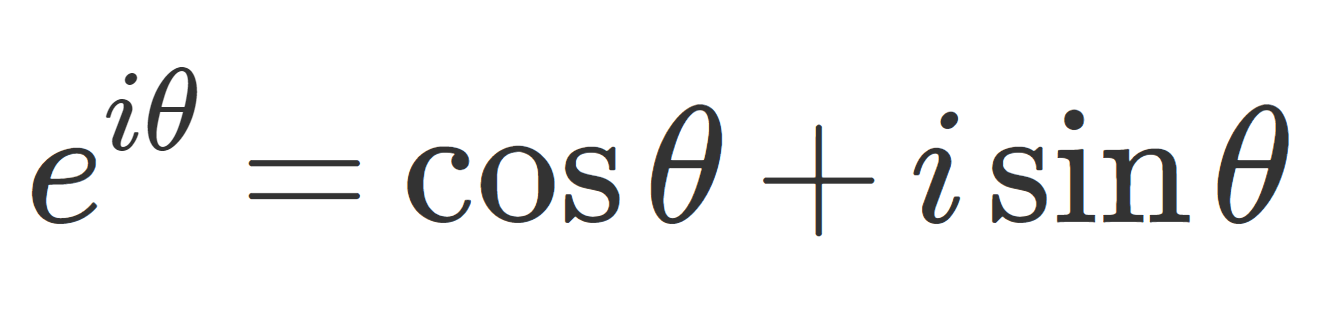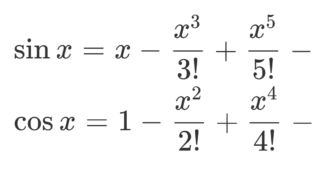オイラーの公式とは, e^{i\theta} = \cos\theta+i\sin\theta で,オイラーの等式とは,それに \theta = \pi を代入した等式 e^{i\pi} =-1 を指します。
これらの公式・等式がどういった意味で成立するのか,その証明と関連公式の解説を行いましょう。
オイラーの公式・オイラーの等式とは
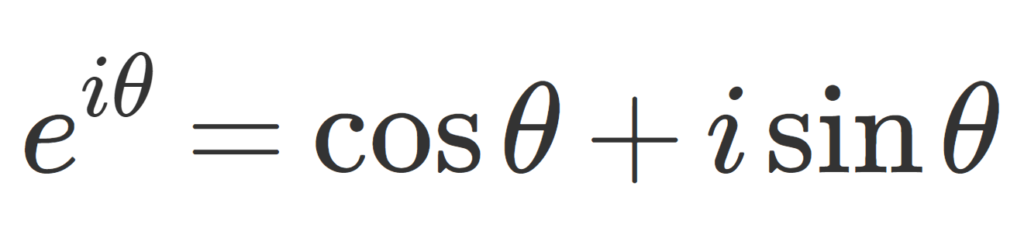
オイラーの公式・オイラーの等式
定理(オイラーの公式; Euler’s formula)
\theta \in\mathbb{R} について,
\large\color{red} e^{i\theta} = \cos\theta+i\sin\theta
である。
ここで,等式に e^{i\theta} というのが出てきていますね。これの定義は,指数関数 e^x のマクローリン展開を複素数に拡張して,
e^{i\theta} = 1+i\theta+ \frac{(i\theta)^2}{2!} + \frac{(i\theta)^3}{3!} + \cdots
と定義されます。
ここで,オイラーの公式に \theta=\pi を代入すると, \cos\pi +i\sin\pi = -1 ですから,
\large\color{red} e^{i\pi} =-1
が成り立ちますね。これをオイラーの等式 (Euler’s identity) といいます。これは,神秘的な3つの数 i, e, \pi を組み合わせた等式で,美しい等式といわれることも多いです。
高校では,ド・モアブルの定理という名前で, (\cos\theta+i\sin\theta )^n= \cos n\theta+i\sin n\theta というのを習うでしょう。これは,オイラーの公式で解釈すると ( e^{i\theta})^n = e^{i n\theta} という,単に指数の計算を表しています。
オイラーの公式の拡張
オイラーの公式は,さらに以下のように拡張されます。
定理(オイラーの公式の拡張)
z\in\mathbb{C} に対して,
- e^{iz} = \cos z+i\sin z,
- \cos z = \dfrac{e^{iz}+e^{-iz}}{2},
- \sin z = \dfrac{e^{iz}-e^{-iz}}{2i}.
\theta\in\mathbb{R} が z\in\mathbb{C} に拡張されましたね。ここで,各関数の定義は,実数によるマクローリン展開を複素数に拡張したもので,以下の通りです。
収束半径は全て \infty である。
このとき,実数の場合と同様に \cos (-z)= \cos z, \, \sin(-z)=-\sin z が成り立ちますから,定理の1.の式と e^{-iz} = \cos z-i\sin z を組み合わせることで,2,3.も従います。
オイラーの公式の証明
さて,オイラーの公式 e^{i\theta} =\cos\theta +i\sin\theta を証明しましょう。 証明自体は,そんなに難しくありません。
証明
\theta \in\mathbb{R} とする。
\begin{aligned}&e^{i\theta}\\ &= \sum_{n=0}^\infty \frac{(i\theta)^n}{n!} \\ &= \lim_{N\to\infty} \sum_{n=0}^{2N} \frac{(i\theta)^n}{n!} \\ &= \lim_{N\to\infty} \left( \sum_{n=0}^N \frac{(-1)^n \theta^{2n}}{(2n)!} + i\sum_{n=0}^{N-1} \frac{(-1)^n \theta^{2n+1}}{(2n+1)!}\right) \\ &= \sum_{n=0}^\infty \frac{(-1)^n \theta^{2n}}{(2n)!} + i\sum_{n=0}^{\infty} \frac{(-1)^n \theta^{2n+1}}{(2n+1)!} \\ &= \cos\theta +i\sin\theta \end{aligned}証明終
上では,和の順序を交換していますが,あくまで有限和の順序を交換しているだけであり,厳密な証明になっています。
この証明は \theta \in\mathbb{R} を z\in\mathbb{C} に変えても通用します。よって,拡張したオイラーの公式
e^{i z} = \cos z+i\sin z
も証明されますね。