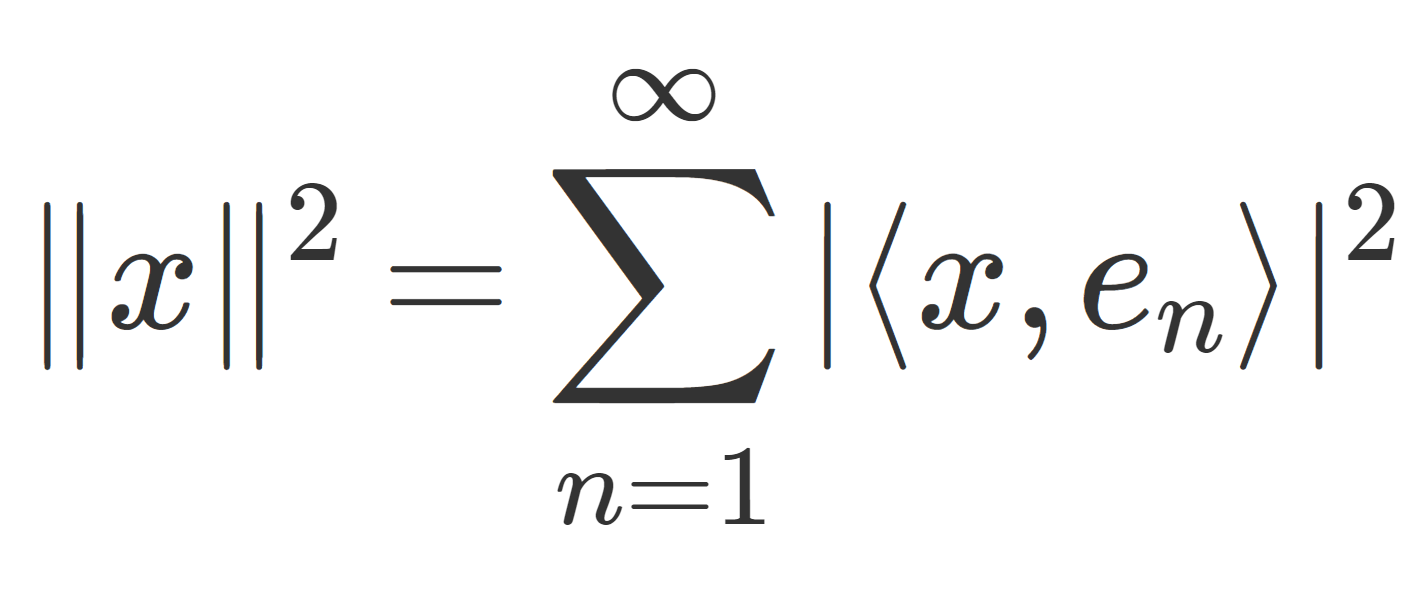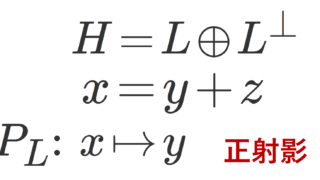パーセバルの等式 (Parseval’s identity) とは,無限次元のピタゴラスの定理(三平方の定理)といえる定理です。パーセバルの等式について,その形と証明を紹介します。
また,フーリエ級数におけるパーセバルの等式はよく使われるため,最後に紹介します。
パーセバルの等式とその発展
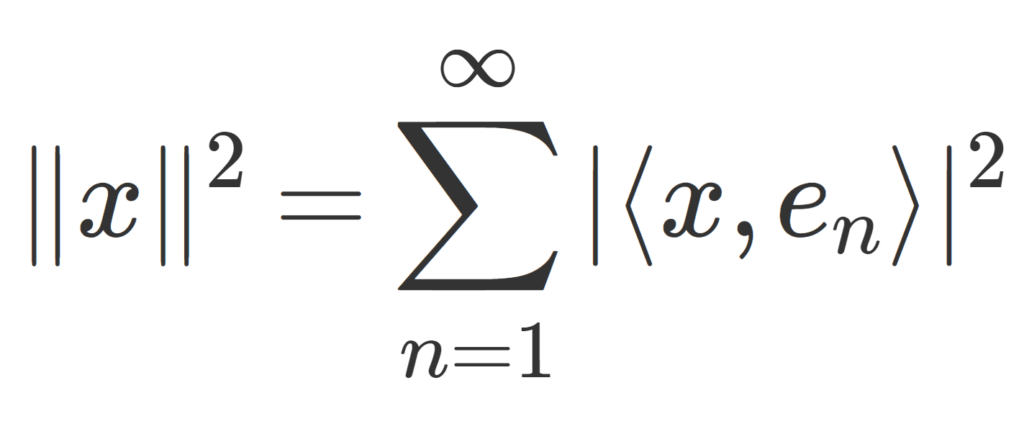
まず関数解析の側面から,パーセバルの等式の一般的な話を進めましょう。
パーセバルの等式とその証明
本記事では,ベクトル a,b の内積を \langle a,b\rangle と表記します。 \{e_n\} が正規直交系 (orthonormal system) とは,
\langle e_m, e_n\rangle=\begin{cases} 1 & m=n, \\ 0 & m\ne n\end{cases}
が成り立つことで,正規直交基底 (orthonormal basis) とは,全てのベクトルが \{e_n\} の線形結合(無限和)で書けること,難しく言うと \overline{\operatorname{Span} \{e_n\}} が全体空間になることを言うのでした(→正規直交系・正規直交基底)。
パーセバルの等式1 (Parseval’s identity)
H をヒルベルト空間とし, \{e_n\}_{n=1}^\infty \subset H はその正規直交基底とする。このとき,任意の x\in H に対し,
\Large \color{red}\| x\|^2=\sum_{n=1}^\infty |\langle x, e_n\rangle |^2
が成り立つ。
パーセバルの等式は,三平方の定理,ピタゴラスの定理の無限次元バージョンって感じです。有限次元バージョンは正規直交系・正規直交基底の記事の後半の方で証明していますが,さらにそれを無限次元に拡張したものになります。
ちょっと何を言っているか分からない,という場合は,正規直交系への正射影のイメージがあれば分かりやすいです。以下の後半で解説しています。
パーセバルの等式の証明
\{e_n\}\subset H より,上の記事から x=\sum_{n=1}^\infty \langle x, e_n\rangle e_n と表せる。同じ上の記事から,
\langle x,x\rangle =\sum_{n=1}^\infty \langle x, e_n\rangle \overline{\langle x, e_n\rangle}
すなわち,\| x\|^2=\sum_{n=1}^\infty |\langle x, e_n\rangle |^2 が言える。
証明終
なお, \{e_n\}\subset H を正規直交基底ではなく,正規直交系に置き換えたときに成り立つ不等式 \color{red} \| x\|^2 \le \sum_{n=1}^\infty |\langle x, e_n\rangle |^2 をベッセルの不等式 (Bessel’s inequality) といいます。パーセバルの等式を理解できるならば,ベッセルの不等式は簡単に見えると思います。証明もより簡単にできます。
パーセバルの等式の非可算無限への拡張
前節のパーセバルの等式は,ヒルベルト空間は可算濃度の正規直交基底を持つと仮定しました。これは,非可算濃度にしても成立します。
パーセバルの等式2 (Parseval’s identity)
H をヒルベルト空間とし, \{e_\lambda\}_{\lambda\in \Lambda} \subset H はその正規直交基底とする。このとき,任意の x\in H に対し,
\Large \color{red}\| x\|^2=\sum_{\lambda\in \Lambda} |\langle x, e_\lambda\rangle |^2
が成り立つ。
\{e_\lambda\}_{\lambda\in \Lambda} \subset H が非可算集合であったとしても, \langle x, e_\lambda \rangle \ne 0 となる \lambda 全体の集合 F は高々可算個です。したがって,上式の右辺の和は意味を持ち,結局やっていることは同じというわけです。
念のため, \langle x, e_\lambda \rangle \ne 0 となる \lambda 全体の集合 F は高々可算個しかないことを確認しておきましょう。ベッセルの不等式より,任意の有限集合 S\subset \Lambda に対して, \sum_{\lambda\in S} |\langle x, e_\lambda\rangle |^2\le \|x\|^2 ですから, |\langle x, e_\lambda \rangle|^2 \ge \|x\|^2/n となる \lambda の集合 F_n は高々 n 個の要素しか持ちません。
F = \bigcup_{n=1}^\infty F_n
ですから, F は高々可算個ですね。
パーセバルの等式と正規直交系・正規直交基底
正規直交系・正規直交基底については,より一般に以下の定理が成立します。ちょっと話がそれますが,紹介しておきましょう。
定理(正規直交系が正規直交基底である条件)
H をヒルベルト空間, \{e_\lambda\}_{\lambda \in \Lambda} \subset H を正規直交系とする。このとき,以下は同値である。
- \{e_\lambda\}_{\lambda \in \Lambda} は正規直交基底である
- \displaystyle x=\sum_{\lambda\in \Lambda} \langle x, e_\lambda\rangle e_\lambda ,\quad x\in H
- \displaystyle \| x\|^2=\sum_{\lambda\in \Lambda} |\langle x, e_\lambda \rangle |^2 (パーセバルの等式)
- \displaystyle \langle x,y\rangle =\sum_{\lambda\in \Lambda} \langle x, e_\lambda \rangle \overline{\langle y, e_\lambda \rangle} ,\quad x,y\in H
- \color{red} \langle x, e_\lambda \rangle =0 \;(\lambda\in \Lambda)\implies x=0
特に5.が面白いと思うのですが,どうでしょうか。軽く証明しておきましょう。
証明
1. \implies 2,3,4.はヒルベルト空間における正射影・正射影作用素で証明した。また,2,3,4. \implies 5.は明らか。
5. \implies 1.を示す。5.を仮定する。 L=\overline{\operatorname{Span} \{e_\lambda\}} とする(Spanの閉包)と,ヒルベルト空間における射影定理より, H=L\oplus L^\perp である。
5.の仮定から, L^\perp =\{0\} より, H=L なので,1.が成立する。
証明終
フーリエ級数におけるパーセバルの等式
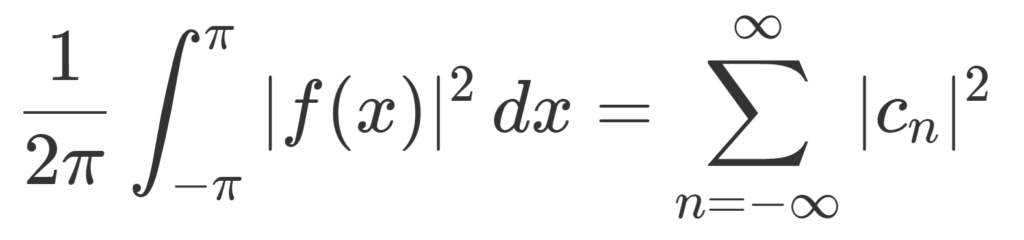
フーリエ級数におけるパーセバルの等式はよく使われますので,特別に述べておくことにします。
フーリエ級数におけるパーセバルの等式
f\in L^2[-\pi,\pi] とする。すなわち,関数 f\colon [-\pi,\pi] \to\mathbb{C} は \int_{-\pi}^\pi |f(x)|^2\, dx<\infty をみたすとする。このとき,
\color{red} \frac{1}{2\pi} \int_{-\pi}^\pi |f(x)|^2\, dx = \sum_{n=-\infty}^\infty |c_n|^2.
ただし, \displaystyle c_n = \frac{1}{2\pi}\int_{-\pi}^\pi f(x) e^{-inx}\, dx とした。
なお, e^{inx}=\cos nx+i\sin nx なので,
\begin{aligned}p_n&= \frac{1}{2\pi}\int_{-\pi}^\pi f(x) \cos nx \, dx,\\ q_n&= \frac{1}{2\pi}\int_{-\pi}^\pi f(x) \sin n x\, dx \end{aligned}
と定めると,
とかくことも可能です。
証明
f,g \in L^2[-\pi,\pi] に対し,
\langle f, g\rangle =\frac{1}{2\pi} \int_{-\pi}^\pi f(x) \overline{g(x)}\, dx
とすると, L^2[-\pi,\pi] はヒルベルト空間になる。ここで, e_n(x) =e^{inx} とすると, \{e_n\} は正規直交基底となる。ここで,
であるから,パーセバルの等式 \| f\|^2=\sum_{n=1}^\infty |\langle f, e_n\rangle |^2 に当てはめることで結論を得る。
証明終