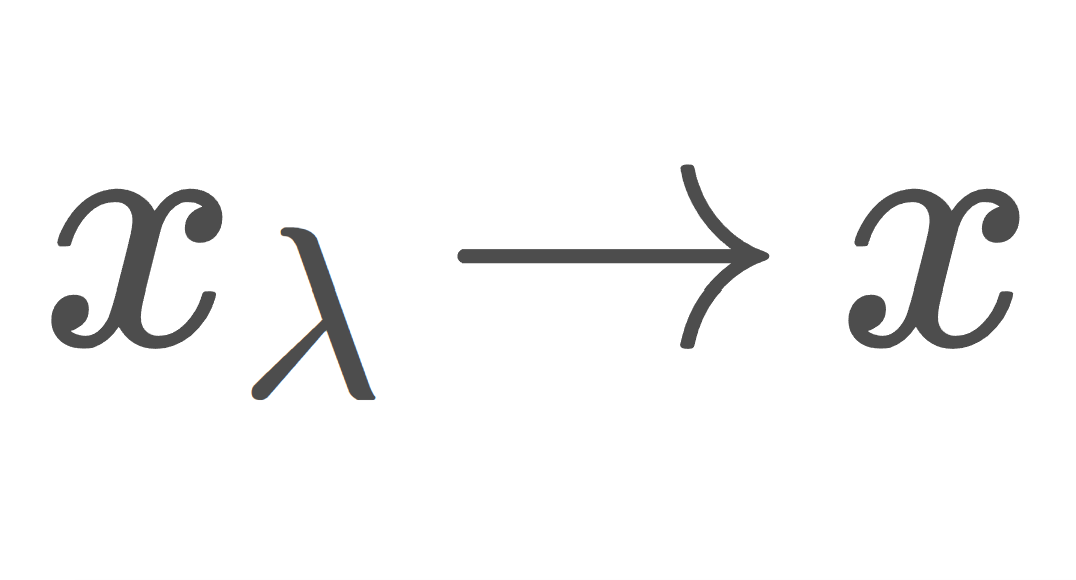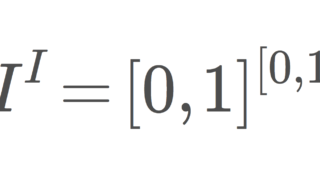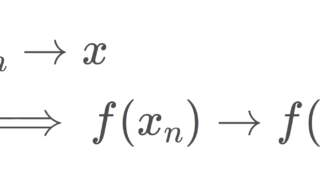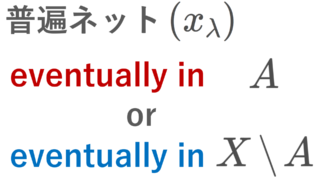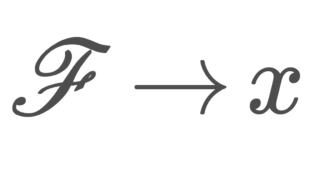正の整数を添え字とする点列について，添え字をより一般の有向集合に変えたものをネットあるいは有向点族・有向点列といいます。一般の位相空間を扱うにあたって，点列では不十分であることが知られていますが，ネットであれば，一般の位相空間を特徴づけることができます。
ネットについて，定義から位相の特徴づけまで，証明付きで，かつ点列では不十分であることも確認しながら，進めていきましょう。
ネット(有向点族)の定義と諸概念
点列 (x_n) の添え字 n\in\mathbb{N} を有向集合 \lambda\in \Lambda に一般化したものがネットです。まずは有向集合の定義を復習し，それからネット・部分ネットの定義，さらに収束の概念まで一気に確認しましょう。
0. 添え字となる有向集合の定義
たとえば，正の整数全体の集合は有向集合の一つです。有向集合は，前順序集合でかつ任意の2元の上界が存在するようなものをいいます。「任意の2元の上界の存在」により，正の整数で言う n\to\infty のようなことを考えることができ，点列の収束の概念を一般化することが可能です。実際は \Lambda に最大元があれば n\to\infty のようにいくらでも大きくすることはできませんが，最大元がない場合を考えることが多いです。
有向集合の実際の具体例などは，以下の記事で解説しています。
上の記事以外，本記事のネットの具体例のところでも，有向集合の具体例は紹介しています。
1. ネット(有向点族)・点列の定義
実際は位相空間上のネットについて考えますが，ここでは一般の集合の上で定義しましょう。
定義1（ネット・有向点族）
X を空でない集合とし， \Lambda を有向集合とする。さらに， i\colon \Lambda\to X を写像とする。
このとき， (\Lambda, i) の組を X 上のネット (有向点族, 有向点列; net) という。また， \Lambda=\mathbb{N} (正の整数の集合で通常の全順序が入ったもの) のときは点列 (sequence) という。
通常， x_\lambda = i(\lambda) とかいて，その集まりを \color{red}\large (x_\lambda) や \color{red}\large (x_\lambda)_{\lambda\in\Lambda} などとかいてネット(有向点族)という。
x_\lambda とかくのは， X の元であることをわかりやすくするためで，要するにネット (x_\lambda) とは，有向点族 \Lambda で添え字付けれた X の部分集合のことです。それを厳密に定義しようとすると，写像 \lambda\mapsto x_\lambda を考えることになります。添え字が自然数 \mathbb{N} のときは (x_n) とかき，これは点列と言います。
定義する前にも述べましたが，点列の添え字 n\in\mathbb{N} を有向集合 \lambda\in \Lambda に一般化したものがネットなわけです。
ネットの具体例を先に確認したい場合は，「ネット(有向点族)にまつわる具体例」のところまで飛んでください。
2. 部分ネットの定義
部分列（部分点列）と似たような感じで，部分ネットの概念を導入します。
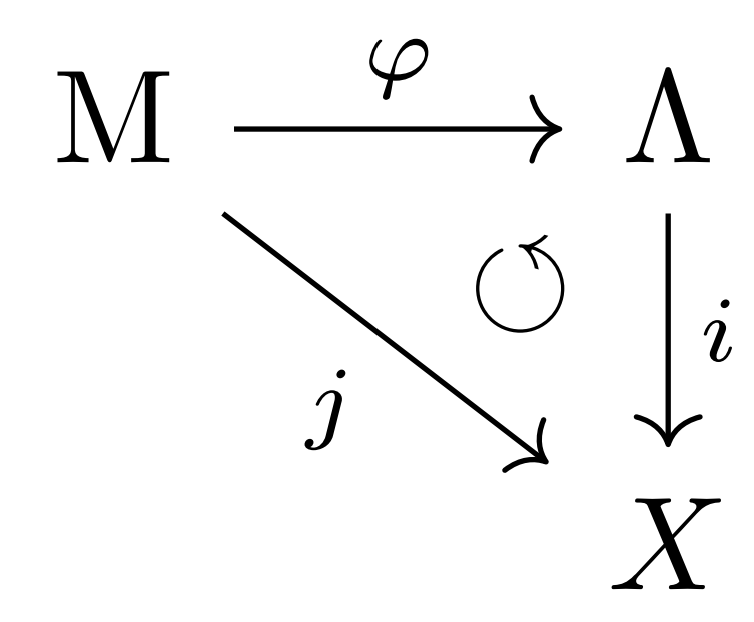
定義2（部分ネット）
X を空でない集合とし， (\Lambda, i) を X 上のネット(有向点族)とする。
X 上のネット (\Mu, j) が (\Lambda, i) の部分ネット (部分有向点族, 部分有向点列; subnet) であるとは，次の条件をみたす \varphi\colon \Mu\to \Lambda が存在することをいう。
- j=i\circ\varphi
- 任意の \mu_1, \mu_2\in\Mu に対し， \mu_1\le \mu_2\implies \varphi(\mu_1)\le \varphi(\mu_2) (単調性)
- 任意の \lambda\in \Lambda に対し，ある \mu\in \Mu が存在して， \lambda\le \varphi(\mu) (cofinal性)
通常， (x_\lambda) の部分ネットを \color{red}\large (x_{\varphi(\mu)}) や \color{red}\large (x_{\lambda_\mu}) のようにかく。
最後の記述は，点列 (x_n) の部分列を (x_{n_k}) とかくのに似ていますね。
注意ですが上の定義2中の「ネット」を全て「点列」に変えても，部分列（部分点列）の定義にはなりません。
点列 (\mathbb{N}, j) が，点列 (\mathbb{N},i) の部分列 (部分点列; subsequence) であるとは，次の条件をみたす \varphi\colon \mathbb{N}\to\mathbb{N} が存在することをいいます。
- j=i\circ\varphi
- 任意の k_1, k_2\in\mathbb{N} に対し， k_1\textcolor{red}{<} k_2\implies \varphi(k_1)\textcolor{red}{<} \varphi(k_2) (狭義単調性)
- 任意の n\in\mathbb{N} に対し，ある k\in\mathbb{N} が存在して， n\le \varphi(k) (cofinal性)
異なる部分を赤字で示しました。たとえば， (x_{n_k}) が点列 (x_n) の部分ネットというときには，
k(1)=k(2)<k(3)=k(4)<k(5)=k(6)<\cdots
というのが許容されますが，点列では許容されません。他にも， r\mapsto \max\{ 1, \lfloor r \rfloor\}=n_r としたとき，( \lfloor\,\cdot\, \rfloor は床関数(ガウス記号)) (x_{n_r})_{r\in\R} は点列 (x_n) の部分ネットです。
このことからもわかると思いますが， (\Mu, j) が (\Lambda, i) の部分ネットというときに，\Mu の濃度が \Lambda の濃度よりも大きくなることもあります。ただし， X の部分集合と見たときに， (x_{\lambda_\mu})\subset (x_\lambda) になることに変わりありません。
また，cofinal性があるのは，たとえば x_1, x_1, x_1,\ldots という点列を部分ネットとは言いたくないからです。 (x_\lambda) から部分的にとってきたとしても，もとが \lambda\to \infty みたいなものが考えられるなら，ちゃんと部分列の添え字でも \lambda_\mu\to \infty みたいになってほしいですよね。
3. ネット(有向点族)の収束・集積点の定義
さて，一般の位相空間におけるネット・点列の収束の定義をしましょう。その前に準備をします。
定義3（eventually in, frequently in）
(X,\mathcal{O}) を位相空間とし， (x_\lambda)_{\lambda\in \Lambda} \subset X をその上のネット(有向点族)とする。さらに A\subset X とする。
- (x_\lambda) is eventually in A とは，ある \lambda_0\in \Lambda が存在して，
\lambda\ge \lambda_0 \implies x_\lambda\in A
が成り立つことをいう。 - (x_\lambda) is frequently in A とは，任意の \lambda_0\in \Lambda に対し，ある \lambda\ge \lambda_0 が存在して， x_\lambda\in A が成り立つことをいう。
eventually とは日本語では「最終的に」と訳されますが，要するに \lambda を十分大きくすれば，「最終的に」ずっと A に入るようになるというイメージです。
また，frequently とは日本語では「頻繁に」と訳されますが，要するに \lambda をどれだけ大きくしても，無限に x_{\lambda'}\in A となる \lambda'>\lambda が取れるということです。
定義より明らかに， (x_\lambda) is eventually in A \implies (x_\lambda) is frequently in A です。
また， (x_\lambda) is eventually in A \iff (x_\lambda) is not frequently in X\setminus A です。逆に， (x_\lambda) is not eventually in A \iff (x_\lambda) is frequently in X\setminus A がいえます。
定義4（ネットの収束・集積点）
(X,\mathcal{O}) を位相空間とし， (x_\lambda)_{\lambda\in \Lambda} \subset X をその上のネット(有向点族)とする。
x\in X の任意の開近傍 U_x に対し， (x_\lambda) is eventually in U_x となるとき， (x_\lambda) は x に収束する (converge) といい，\large\color{red} x_\lambda\to x あるいは \lim x_\lambda=x とかく。
x\in X の任意の開近傍 U_x に対し， (x_\lambda) is frequently in U_x となるとき，x は (x_\lambda) の集積点 (accumulation point, cluster point) であるという。
注意ですが，収束先は1点とは限りません。たとえば，密着空間 (X,\{\emptyset, X\}) においては，全ての点 x\in X の開近傍が X のみなので， X 上のネットは全ての点に収束するといえます。後の定理5で紹介しますが，収束先が1点である必要十分条件は，ハウスドルフ空間( T_2 空間)であることです。
また，常に x_\lambda=x である定ネットでは，明らかに x_\lambda\to x です。
点列の収束・集積点も全く同じように定義されます。
ネット(有向点族)にまつわる具体例
具体例を紹介しましょう。
例1( I^I ).
I=[0,1] を単位閉区間とし，直積位相 I^I を考える。これは，
I^I=\{f\mid f\colon I\to I\}
に，各点収束の位相を入れた空間である(→I^I の位相的性質～コンパクトだが点列コンパクトでない例～)。
と定義すると， I^I そのものが有向集合であり，(定義1において i\colon I^I\to I^I を恒等写像と思うことで) I^I 自身がネットである。このネットを (f)_{f\in I^I} とかくことにする。
f\to \boldsymbol{1} である。ただし， \boldsymbol{1} とは，任意の x\in [0,1] に対し， \boldsymbol{1}(x)=1 となる関数 \boldsymbol{1}\colon I\to I を指すものとする。
A\subset I^I を，有限個の x\in [0,1] のみで 1，それ以外で 0 となる関数全体の集合
A=\left\{f\in I^I\middle| \begin{aligned} &f(x)=0 \text{ or } 1\text{ and } \\ &f(x)=1 \text{ only finitely often}\end{aligned}\right\}
とすると， A=(f)_{f\in A} も同様にネットである。このときもやはり f\to \boldsymbol{1} である。
(f)_{f\in A} が f\to \boldsymbol{1} となることは，直積位相 I^I の開基が
\begin{aligned} \{f\colon I\to I\mid f(i_1)\in U_1,\ldots, f(i_k)\in U_k\} \end{aligned}
の形でかけること(ただし， k\ge 1,\, i_1, \ldots, i_k\in I,\, U_1, \ldots, U_k は I における開集合)，特に I^I における開集合は， f\colon I\to I における有限個 i_1, \ldots, i_k の行き先しか制限できていない，それ以外の点 i\in I\setminus \{i_1, \ldots, i_k\} では， 0 から 1 までのどんな値を取っても構わないことから， \boldsymbol{1} の任意の開近傍は A と共通部分をもつことから分かります。
I^I における位相的性質は，以下の記事でも解説しています。
例2(近傍系とネット).
(X,\mathcal{O}) を位相空間とし， x\in X とする。
x の開近傍全体の集合を \mathcal{N}_x とすると， \mathcal{N}_x は逆包含順序，すなわち U_1\le U_2\iff U_1\supset U_2 という順序により有向集合になる。
各 U\in \mathcal{N}_x に対し， x_U\in U を一つ選ぶと， (x_U)_{U\in\mathcal{N}_x} は X 上のネットである。
明らかに，このネットは x_U\to x となる。
抽象的ですが，わかりやすい例でしょう。
例3(リーマン和とリーマン積分).
a<b を実数とする。さらに， n\ge 1 とし， a=x_0<x_1<x_2<\cdots< x_n=b をとる。このとき，
\delta=\{x_0,x_1, \ldots, x_n\}
とし，そのような有限集合 \delta 全体の集合を \Delta とすると， \Delta は包含順序 \delta_1\le \delta_2\iff \delta_1\subset \delta_2 により有向集合になる。
f\colon [a,b]\to \R を有界な関数とする。 \delta=\{x_0,x_1, \ldots, x_n\} に対し，
\begin{aligned}S_\delta f &= \sum_{k=1}^n\left( \sup_{x_{k-1}\le x\le x_k} f(x)\right) (x_k-x_{k-1}), \\ I_\delta f &=\sum_{k=1}^n\left( \inf_{x_{k-1}\le x\le x_k} f(x)\right) (x_k-x_{k-1}) \end{aligned}
とすると， (S_\delta f)_{\delta\in \Delta}, (I_\delta f)_{\delta\in \Delta} はともにネットである。この2つのネットが同じ値に収束するとき， f はリーマン積分可能 (Riemann integrable) といい，その収束値を \int_a^b f(x) \, dx とかく。
リーマン和によるリーマン積分の定義も，実はネットの収束の話をしていたんですね。大学1年生で習うときは，ネットという言葉は使われませんが(→リーマン和による定積分の定義とリーマン積分可能・不可能な例)。
例4(補有限位相).
X を無限集合とし，
\mathcal{O}_f=\{\emptyset\}\cup \{ O\subset X\mid X\setminus O \text{ is finite}\}
を，補集合が有限集合である部分集合全体（と \{\emptyset\} との和集合）とすると， (X,\mathcal{O}_f) は位相空間になる。この位相を補有限位相 (cofinite topology, finite complement topology) という。
補有限位相において， (x_n)\subset X を，どの2点も異なる点列とすると， (x_n) は全ての点に収束する。すなわち，任意の x\in X に対し， x_n\to x である。
x\in X の任意の開近傍 U は， X\setminus U が有限集合であるため，ある N\ge 1 が存在して，n\ge N\implies x_n\in U，すなわち (x_n) is eventually in U となります。 よって， x_n\to x といえますね。
補有限位相は T_1 ですが，ハウスドルフ( T_2)ではありません。後の定理5で紹介しますが，収束する任意のネットの収束点が1点のみである必要十分条件は， X がハウスドルフ( T_2)であることです。本例は， T_1 だと収束点が1点とは限らない例です。
例5(シェルピンスキー空間).
2点集合 S=\{0,1\} について，その上の開集合族を
\mathcal{O}=\Bigl\{ \emptyset, \{0\}, \{0,1\}\Bigr\}
としたときの位相空間 (S,\mathcal{O}) をシェルピンスキー空間 (Sierpinski space) という。
- 0,0,0,0,0,\ldots という点列は， 0 にも 1 にも収束する
- 1,1,1,1,1,\ldots という点列は， 1 に収束するが， 0 には収束しない
- 0,1,0,1,0,\ldots という点列は， 1 に収束するが， 0 には収束しない
収束の定義から分かります。
次の例は，順序数と順序位相が分からないと読めませんので， 分からなければ読み飛ばしてください。
例6(順序数による順序位相).
\omega_1 を最小の非可算順序数とし， \omega_1+1=[0,\omega_1] における順序位相を考える。
\omega_1= [0,\omega_1) は全順序集合であるので特に有向集合であるから，ネットである。このネットを (\alpha)_{\alpha\in \omega_1} とかくと， \alpha\to \omega_1 である。
順序位相については，以下で詳しく解説しています。
ネット(有向点族)による位相空間の特徴づけと点列との比較
ネットは，位相空間における多くの概念を特徴づけることができます。紹介していきましょう。点列では特徴づけられないことも一緒に述べます。
1. ネットの集積点 ⇔ 収束部分ネットをもつ
定理1（ネットの集積点 ⇔ 収束部分ネットをもつ）
(X,\mathcal{O}) を位相空間とし， (x_\lambda)_{\lambda\in \Lambda} \subset X をその上のネット(有向点族)とする。このとき，次の2つは同値である。
- x\in X が (x_\lambda) の集積点である
- x \in X に収束する部分ネットが存在する
証明
1.\implies2.について
\Mu = \{ (\lambda, U)\in \Lambda\times \mathcal{N}_x\mid x_\lambda\in U\}
と定め， (\lambda_1, U_1)\le (\lambda_2, U_2)\iff \lambda_1\le \lambda_2\text{ and } U_1\supset U_2 と定義すると， \Mu は有向集合であることを示そう。特に， (\lambda_1, U_1), (\lambda_2, U_2)\in\Mu に対し，上界が存在することを示す。 U_1\cap U_2\in\mathcal{N}_x であることと， (x_\lambda) is frequently in U_1\cap U_2 であることから，ある \lambda が存在して，
とできる。このときの (\lambda, U_1\cap U_2) は上界であるので，\Mu が有向集合であることが示せた。 \varphi\colon \Mu\to \Lambda を \varphi(\lambda, U)=\lambda とすると，これは定義2をみたしているので， (x_\lambda) の部分ネット (x_{\varphi(\mu)}) を定める。この部分ネットが x に収束することを示そう。
U_0\in \mathcal{N}_x とすると， (x_\lambda) is frequently in U_0 より，ある \lambda_0 \in \Lambda が存在して， x_{\lambda_0}\in U_0 である。 \Mu の定義から明らかに
\begin{aligned}&(\lambda,U)\ge (\lambda_0, U_0)\\&\implies x_{\varphi(\lambda, U)}=x_\lambda\in U\subset U_0\end{aligned}
なので， (x_{\varphi(\mu)}) is eventually in U_0 である。よって， (x_{\varphi(\mu)}) は x に収束する。
2.\implies1.について
(x_{\varphi(\mu)}) を収束部分ネットとする。 U\in \mathcal{N}_x に対し， (x_{\varphi(\mu)}) is eventually in U なので，ある \mu_0 が存在して，
\mu\ge \mu_0\implies x_{\varphi(\mu)}\in U
とできる。任意の \lambda_0\in\Lambda に対し， \varphi(\mu)\ge \lambda_0 となる \mu\ge \mu_0 を選ぶと， x_{\varphi(\mu)}\in U なので， (x_\lambda) is frequently in U である。よって， (x_\lambda) は x を集積点にもつ。
証明終
なお，点列 (x_n) について，x\in X が (x_n) の集積点だとしても， x に収束する部分点列が存在するとは限りません。 x に収束する (x_n) の部分ネットであれば上記定理より存在します。ただし， X が第一可算なときは，部分点列が存在します。
2. ネットと閉集合
定理2（ネットと閉集合）
(X,\mathcal{O}) を位相空間とし， A\subset X とする。このとき，1. \iff 2. \impliedby 3.である。
- x\in \overline{A}
- あるネット (x_\lambda)\subset A で， x_\lambda\to x となるものが存在する
- ある点列 (x_n)\subset A で， x_n \to x となるものが存在する
X が第一可算のときは全て同値である。
証明
1. \implies2.について
x\in\overline{A} のとき，任意の開近傍 U\in \mathcal{N}_x に対し， U\cap A\ne\emptyset であるから， x_U\in U\cap A を選んでくると， (x_U)_{U\in\mathcal{N}_x}\subset A は明らかに x に収束するネットである。
2. \implies1.について
2.のとき， x の任意の開近傍 U\in\mathcal{N}_x に対し，x_\lambda \in U \cap A となる \lambda が存在するので，特に U\cap A\ne\emptyset であるから， x\in \overline{A} である。
3. \implies2.は，点列はネットの一種であることから明らか。
第一可算のときの1.\implies 3.について
第一可算より， x の基本近傍系を
U_1\supset U_2\supset U_3\supset\cdots
とできる。 x\in \overline{A} より，各 n\ge 1 で U_n\cap A\ne\emptyset である。よって， x_n \in U_n\cap A を選んでくると， (x_n)\subset A は明らかに x に収束する点列である。
証明終
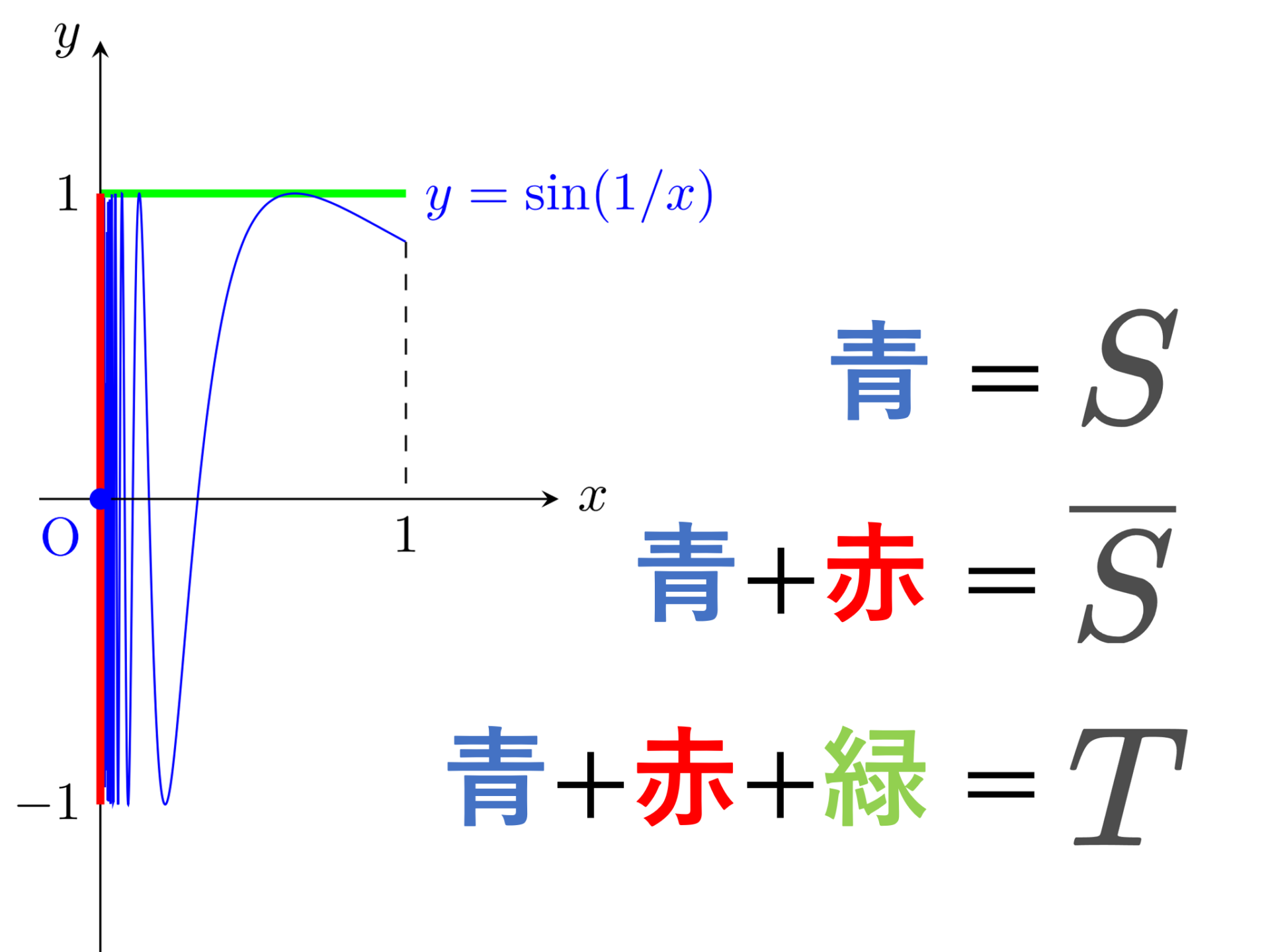
なお，第一可算でないときは，1.\implies3.は成立しません。例1.で紹介した， I^I における
A=\left\{f\in I^I\middle| \begin{aligned} &f(x)=0 \text{ or } 1\text{ and } \\ &f(x)=1 \text{ only finitely often}\end{aligned}\right\}
がその例です。 \boldsymbol{1} を，任意の x\in [0,1] に対し， \boldsymbol{1}(x)=1 となる関数 \boldsymbol{1}\colon I\to I を表すこととすると，\overline{A}=\boldsymbol{1} だし，ネット (f)_{f\in A} は f\to \boldsymbol{1} となります。
一方で，点列 (f_n)\subset A で， f_n\to \boldsymbol{1} となるものはありません。 I^I における位相は各点収束であることに注意してください(→I^I の位相的性質～コンパクトだが点列コンパクトでない例～)。
もし，点列 (f_n)\subset A が I^I の位相で収束，すなわち各点収束したとすると， f_n(x)=1 となる x は有限個しかないので， f_n が 0,1 のどちらかの値しかとらないことに注意すると，収束先の関数 f は， f(x)=1 となる x は高々可算個のはずです。しかし，関数 \boldsymbol{1} はそうはなっていないですね。
また，例6.における [0,\omega_1)\subset [0,\omega_1] もその例で，\overline{[0,\omega_1)}=[0,\omega_1] ですが，点列 (x_n)\subset [0,\omega_1) で， x_n\to \omega_1 となるものは存在しません(→順序位相の定義と順序数における順序位相の性質)。
3. ネットと連続写像
定理3（ネットと連続写像）
X, Y を位相空間とし，f\colon X\to Y とする。このとき，1. \iff 2. \implies 3.である。
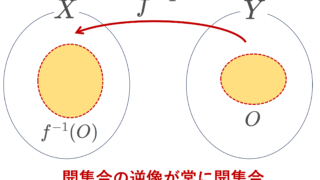
- f は x\in X で連続。すなわち， f(x)\in Y の任意の近傍 N\subset Y の逆像 f^{-1}(N)\subset X が x\in X の近傍である
- x_\lambda \to x となる任意のネット (x_\lambda)_{\lambda\in\Lambda}\subset X に対し， f(x_\lambda)\to f(x) となる
- x_n \to x となる任意の点列 (x_n)\subset X に対し， f(x_n)\to f(x) となる（点列連続; sequentially continuous）
X が第一可算のときは全て同値である。
(f(x_\lambda))_{\lambda\in\Lambda} は Y におけるネットであることに注意してください。
証明
1.\implies 2.について
x_\lambda\to x となるネット (x_\lambda) を考える。 f(x)\in Y の近傍 N\subset Y を任意にとる。f^{-1}(N)\subset X は x の近傍なので，ある \lambda_0 が存在し，
\lambda\ge \lambda_0\implies x_\lambda \in f^{-1}(N)
となる。このとき， f(x_\lambda)\in N なので， (f(x_\lambda)) is eventually in N となる。ゆえに， f(x_\lambda)\to f(x) である。
2.\implies 1.について
対偶を示す。 f が x\in X で連続でないとすると， f(x)\in Y のある近傍 N\subset Y で， f^{-1}(N)\subset X が x の近傍でないものが存在する。このとき， x\notin \operatorname{Int}(f^{-1}(N)) (Intは内部(開核)を指す)なので，
x\in X\setminus \operatorname{Int}(f^{-1}(N))=\overline{X\setminus f^{-1}(N)}
である。定理1より，あるネット (x_\lambda)\in X\setminus f^{-1}(N) で， x_\lambda\to x となるものが存在するが，このとき， f(x_\lambda)\notin N なので， f(x_\lambda) \nrightarrow f(x) である。
2.\implies 3.については，点列はネットの一種であることから明らか。
第一可算のときの3.\implies 1.について
対偶を示す。 f が x\in X で連続でないとする。上の 2.\implies 1.の証明と同様にして，定理1より， x_n\to x がとれるが，このとき， f(x_n) \nrightarrow f(x) なので，点列連続でない。
証明終
なお，第一可算でないときは，3.\implies1.は成立しません。点列連続だけど連続でない例は，以下の記事で紹介しています。
4. ネットと直積位相
定理4（ネットと直積位相）
\{(X_\alpha,\mathcal{O}_\alpha)\}_{\alpha\in\Alpha} を位相空間の族とする。さらに， X=\prod_{\alpha\in\Alpha} X_\alpha における直積位相を考え， p_\alpha \colon X\to X_\alpha を自然な射影とする。
(x_\lambda)_{\lambda\in\Lambda}\subset X をネットとし， x\in X とする。このとき，次の2つは同値である。
- x_\lambda\to x
- 任意の \alpha\in \Alpha に対し， p_\alpha(x_\lambda)\to p_\alpha(x)
この定理は直積位相を扱うにあたって，使いやすい定理です。
証明
1.\implies 2.について
p_\alpha が連続であることと，定理3より言える。
2.\implies 1.について
U を x の開近傍とすると，直積位相の定義より， ある n\ge 1 と \alpha_1,\ldots, \alpha_n\in \Alpha と， U_1\in \mathcal{O}_{\alpha_1}, \ldots ,U_n\in\mathcal{O}_{\alpha_n} が存在して，
x\in \prod_{k=1}^n U_k \times\prod_{\alpha\in \Alpha\setminus\{\alpha_1,\ldots, \alpha_n\} }X_\alpha\subset U
とできる。真ん中の集合を B とする。 (x_\lambda)_{\lambda\in\Lambda} is eventually in B を示そう。2.の仮定より，各 1\le k\le n に対して，ある \lambda_k が存在して，
とできる。 \lambda'=\max\{ \lambda_1,\ldots, \lambda_n\} とおくと，全ての 1\le k\le n に対して，
とできる。すなわち， \lambda\ge \lambda'\implies x_\lambda\in B となるから， (x_\lambda)_{\lambda\in\Lambda} is eventually in B である。よって， x_\lambda\to x である。
証明終
5. ネットと分離公理～収束先の一意性～
定理5（ネットと分離公理～収束先の一意性～）
(X,\mathcal{O}) を位相空間とする。このとき，次の2つは同値である。
- X はハウスドルフ空間( T_2 空間)である
- ネットが収束するとき，その収束先は必ず1点のみである
証明
1.\implies 2.について
ネット (x_\lambda)\subset X が x_\lambda\to x\in X となるとする。 y\in X を y\ne x とすると， X はハウスドルフ空間なので，ある x\in X の開近傍 U と y\in X の開近傍 V で U\cap V\ne \emptyset となるものが存在する。
(x_\lambda) is eventually in U なので， (x_\lambda) is not eventually in V であり，これより， (x_\lambda) は y に収束し得ない。
よって， (x_\lambda) の収束先は x のみである。
2.\implies 1.について
X がハウスドルフでないと仮定する。このとき，ある異なる2点 x,y\in X が存在して， x,y の開近傍全体の集合 \mathcal{N}_x, \mathcal{N}_y を考えると，任意の U\in \mathcal{N}_x, \, V\in \mathcal{N}_y に対し， U\cap V\ne \emptyset とできる。よって， x_{U, V}\in U\cap V を選ぶことができる。
\mathcal{N}_x, \mathcal{N}_y には，逆包含順序が入っているものとし，さらに \mathcal{N}_x\times \mathcal{N}_y に積順序，すなわち
\begin{aligned}&(U_1, V_1)\le (U_2, V_2)\\&\iff U_1\le U_2\text{ and } V_1\le V_2\end{aligned}
という順序が入っているものとすると，この順序により \mathcal{N}_x\times \mathcal{N}_y は有向集合になる。ネット (x_{U, V})_{(U, V)\in \mathcal{N}_x\times \mathcal{N}_y} は， x, y の両方に収束するが，これは2.の仮定に矛盾する。
ゆえに， X はハウスドルフである。
証明終
X がハウスドルフ( T_2)空間ではなく， T_1 空間のときは，収束点が1点とは限りません。例4.がその例です。
6. ネットとコンパクト性
定理6（ネットとコンパクト性）
(X,\mathcal{O}) は位相空間とする。このとき，以下は同値
- X はコンパクト
- X 上の任意のネットが収束する部分ネットをもつ
- X 上の任意のネットが集積点をもつ
2. \iff 3.については，定理1と同じです。1.\iff 3.を示しましょう。
証明
1.\implies 3.について
(x_\lambda)_{\lambda\in\Lambda}\subset X をネットとする。
F_\lambda =\overline{\{x_\mu \mid \mu\ge \lambda\}}
とおくと， \{ F_\lambda\}_{\lambda\in\Lambda} は有限交叉性をもつ。実際， \lambda_1,\ldots, \lambda_n\in \Lambda とすると， \Lambda は有向集合より， \mu\ge \lambda_1,\ldots,\mu\ge \lambda_n となる \mu \in\Lambda がとれ， x_\mu \in \bigcap_{k=1}^n F_{\lambda_k} となるからである。コンパクト性より，x\in \bigcap_{\lambda\in\Lambda} F_\lambda が存在する。
よって， x の任意の近傍 N_x について， (x_\lambda)_{\lambda\in\Lambda} is frequently in N_x なので， x は (x_\lambda)_{\lambda\in\Lambda} の集積点である。
3.\implies1.について
\mathcal{C} を X の開被覆とする。
\Lambda = \{\lambda \subset \mathcal{C}\mid \lambda \text{ is finite}\}
を有限部分集合の族とすると，\Lambda は包含関係によって有向集合である。 X がコンパクトでないとすると，任意の \lambda\in \Lambda に対し，
が取れる。ネット (x_\lambda) は3.の仮定より集積点 x\in X をもつ。 \mathcal{C} は開被覆より，\bigcap_{C\in\mathcal{C}} (X\setminus C)=\emptyset であるが，これは矛盾している。実際， C_x\in \mathcal{C} を x の近傍とすると，x は (x_\lambda) の集積点なので， (x_\lambda) is frequently in C_x である。よって，ある \{C_x\}\le \lambda (すなわち \{C_x\}\subset \lambda )をみたす \lambda が存在して， x_\lambda \in C_x とならねばならないが， x_\lambda はその取り方から C_x には入らないので，矛盾している。
証明終
ネットは位相的性質が直感的に扱えて良いですね。
