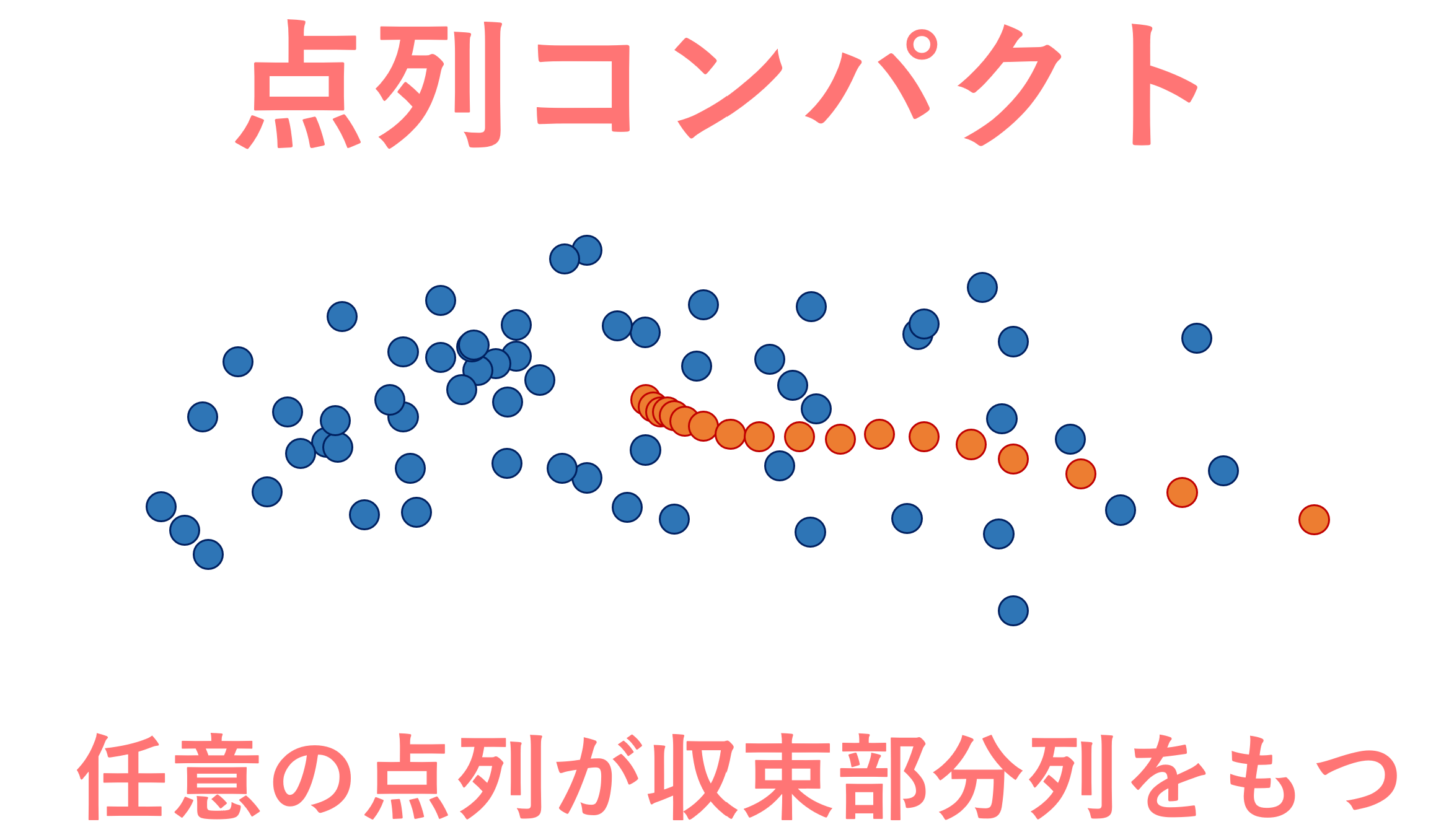
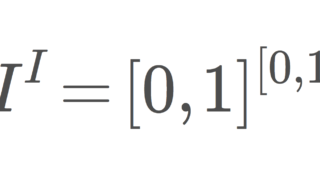点列コンパクトとは,任意の点列が収束部分列をもつような位相空間のことを言います。「点列がコンパクトにまとまっている」ようなイメージの空間で,通常のコンパクト性とも関連があります。
点列コンパクト性について,通常のコンパクト性とも絡めながら,詳しく解説していきましょう。
点列コンパクトの定義
定義(点列コンパクト)
(X,\mathcal{O}) を位相空間とする。任意の点列 (x_n)\subset X が収束部分列をもつとき, X を点列コンパクト (sequentially compact) であるという。
一般のコンパクトは,任意の開被覆が有限部分被覆をもつとして定義されますが,コンパクトは点列を一般化したネット(有向点族)が常に収束部分ネットをもつことと同値です。このネット(有向点族)の点列バージョンが点列コンパクトと考えることができます。
注意ですが,コンパクトと点列コンパクトは別の概念で,どちらが成り立てばもう一方が成り立つというわけではないです。ネット(有向点族)は点列を一般化した概念ですが,収束部分ネットも収束部分列を一般化した概念です。「ネットが常に収束部分ネットをもつ」ならば「点列が常に収束部分ネットをもつ」は言えますが,「点列が常に収束部分列をもつ」とまでは言えません。逆に,「点列が常に収束部分列をもつ」ならば「点列が常に収束部分ネットをもつ」は言えますが,「ネットが常に収束部分ネットをもつ」とまでは言えません。
ただし,距離空間の下では,コンパクトと点列コンパクトは同値です。他に,第二可算の下でも同値です。これについては,後の性質のところで紹介しましょう。
コンパクトに関する諸概念を紹介しておきます。
| 名称 | 定義 |
|---|---|
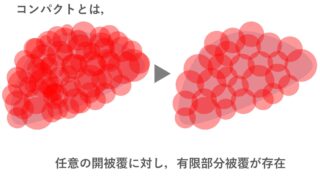
| コンパクト (compact) | 任意の開被覆が有限部分被覆をもつ |
| 局所コンパクト (locally compact) | 任意の点がコンパクトな近傍をもつ |
| 強局所コンパクト (strongly locally compact) | 任意の点がコンパクトな閉近傍をもつ |
| 相対コンパクト (relatively compact) | 閉包がコンパクトな部分集合 |
| 可算コンパクト (countably compact) | 任意の可算開被覆が有限部分被覆をもつ |
| リンデレーフ (Lindelöf) | 任意の開被覆が可算部分被覆をもつ |
| 点列コンパクト (sequentially compact) | 任意の点列が収束部分列をもつ |
| 極限点コンパクト (limit point compact) | 任意の無限部分集合が集積点をもつ |
| 擬コンパクト (pseudocompact) | この上の任意の実連続関数が有界 |
| σコンパクト (σ-compact) | コンパクト集合の可算和でかける空間 |
| メタコンパクト (metacompact) | 任意の開被覆が点有限な(すなわち,各点ごとに有限個の集合でしか覆われていない)開細分被覆をもつ |
| パラコンパクト (paracompact) | 任意の開被覆が局所有限な(すなわち,各点ごとに有限個の集合でしか覆われていない近傍をもつような)開細分被覆をもつ |
点列コンパクトの具体例
点列コンパクトの具体例を確認するうえで,その他のコンパクト性の概念を紹介しましょう。
例1( I ).
I=[0,1] はコンパクトかつ点列コンパクトである。
I がコンパクトであることはハイネ–ボレルの被覆定理とその証明~有界閉区間のコンパクト性~,点列コンパクトであることはボルツァノ–ワイエルシュトラスの定理とその証明を確認してください。
例2( [0,1) ).
[0,1) はコンパクトでも点列コンパクトでもない。
x_n=1-1/n とすると, x_n\to 1\notin [0,1) なので,点列コンパクトではありません。また,開被覆 \{ [0, 1-1/n)\}_n は有限部分被覆をもたないので,コンパクトでもありません。
コンパクトであることは, I がコンパクトであることと,コンパクト空間の直積はコンパクトであるというチコノフの定理 (Tychonoff’s theorem) から言えます。点列コンパクトでないことを示しておきましょう。
点列コンパクトでない証明
点列コンパクトであると仮定する。このとき, (f_n)\subset I^I を, f_n(i) = ( i を2進展開したときの小数第 n 位の数) と定める。ただし, 1.0000\cdots_{(2)} = 0.1111\cdots_{(2)} などについては左辺を採用する。
もし,収束部分列 (f_{n_k})\subset (f_n) が存在すると仮定する。直積位相 I^I は各点収束位相であることに注意する。 \alpha \in I を,2進展開したときの小数第 n_{2k} 位 ( k\ge 1) を 1,それ以外が 0 となる数とすると,数列 \{ f_{n_k}(\alpha)\}\subset I は 0,1,0,1,0,1\ldots という風になり, I 上で収束しない。これは矛盾である。よって示された。
証明終
I^I の詳しい性質は,以下で解説しています。
例4(順序位相 \omega_1=[0,\omega_1) ).
\omega_1 を最小の非可算順序数とする。このとき, \omega_1=[0,\omega_1) は点列コンパクトであるが,コンパクトでない。
順序位相については,以下で解説しています。点列コンパクトである理由を簡単に言うと, \omega_1 は大きすぎて,点列では \omega_1=[0,\omega_1) からはみ出ることはできない,という感じです。
例5( \omega_1\times I^I ).
直積位相 \omega_1\times I^I は可算コンパクト空間とコンパクト空間の直積なので可算コンパクトである。しかし,コンパクトでも点列コンパクトでもない。
\omega_1 がコンパクトでないし, I^I は点列コンパクトでないので, \omega_1\times I^I はコンパクトでも点列コンパクトでもないです。
点列コンパクトに関する性質
点列コンパクトのときに成り立つ性質をまとめて紹介しましょう。
定理1(点列コンパクトに関する諸性質)
1.と2.については,簡単なので省略します。2.は連続 \implies 点列連続を用います。
3.については,可算コンパクトの定義・性質と証明・具体例で示しています。
4.については,コンパクトなら可算コンパクトであることと,3.より成立します。
5.については,点列コンパクトなら可算コンパクトであることを踏まえて,可算コンパクトの定義・性質と証明・具体例の記事で示しています。
なお,ハウスドルフ空間( T_2 空間)における,コンパクト部分集合は閉ですが,点列コンパクトな部分集合は閉集合とは限りません(コンパクトな部分集合は閉集合です)。たとえば,例4.を [0,\omega_1)\subset [0,\omega_1] とみたとき, [0,\omega_1) は点列コンパクトですが,閉集合ではありません。
6.について簡単に示しましょう。 (x_n) を直積空間における点列とすると,第一成分が収束するように部分列 (x_n^{(1)})\subset (x_n) が取れます。次に第二成分が収束するように部分列 (x_n^{(2)})\subset (x_n^{(1)}) が取れます。次に第三成分が収束するように部分列 (x_n^{(3)})\subset (x_n^{(2)}) が取れます。これを帰納的に繰り返します。
このとき,点列 (x_n^{(n)}) を考えると,これは任意の成分で収束します(対角線論法)。直積空間における点列の収束の位相は,各成分の収束の位相なので, (x_n^{(n)}) は直積空間上収束すると言えました。
距離空間におけるコンパクトとの同値性
距離空間なら,もっと話はシンプルです。
定理2(距離空間におけるコンパクトとの同値性)
(X, d) を距離空間とする。このとき,以下は同値である。
また,上のいずれか(したがって全て)が成立するとき,次の3つが成立する。
上の3つは一般の距離空間において同値である。
後半の3つが一般の距離空間において同値であることは,第二可算公理と第二可算な位相空間の例・性質で証明しています。
本記事では,最初の5つの同値性について簡単に証明しましょう。以下で, \varepsilon>0 に対し, a\in X における \varepsilon-近傍を
B_\varepsilon(a)=\{x\in X\mid d(a,x)<\varepsilon\}
とかくことにします。
証明
3. \iff4.について
距離空間は T_1 分離公理をみたし, T_1 の下では,3.と4.は同値(→可算コンパクトの定義・性質と証明・具体例)なので示せた。
2.\iff 3.,1.\implies 2.について
2. \implies 5.について
点列コンパクトの定義よりコーシー列が収束せねばならないので,明らかに完備である。全有界でないと仮定する。このとき,ある \varepsilon>0 が存在して,次をみたす点列 (a_n)_{n=1}^\infty を帰納的に構成できる。
a_n\notin B_\varepsilon(a_1)\cup B_\varepsilon(a_2)\cup \cdots\cup B_\varepsilon(a_{n-1})
(a_n) は集積点をもたないので,点列コンパクト性に反する。よって,点列コンパクトならば全有界である。
全有界 \implies 可分について
各 n\ge 1 に対し,ある a^{(n)}_1, a^{(n)}_2,\ldots,a^{(n)}_{k_n} が存在して,
X=B_{\frac{1}{n}}(a^{(n)}_1)\cup B_{\frac{1}{n}}(a^{(n)}_2)\cup \cdots\cup B_{\frac{1}{n}}(a^{(n)}_{k_n})
とできる。このときの (a^{(n)}_{i})_{1\le i\le k_n, \, n\ge 1} は可算集合で稠密なので, X は可分である。
5.\implies 2.について
(x_m)\subset X を任意の点列とする。 X は全有界なので,各 n\ge 1 に対し,ある a^{(n)}_1, a^{(n)}_2,\ldots,a^{(n)}_{k_n} が存在して,
X=B_{\frac{1}{n}}(a^{(n)}_1)\cup B_{\frac{1}{n}}(a^{(n)}_2)\cup \cdots\cup B_{\frac{1}{n}}(a^{(n)}_{k_n})
とできる。 n=1 とする。いずれかの B_1(a^{(1)}_i) で, (x_m) を無限個含むものがある。 i が複数ある場合はそのうちの一つを選び, (x_m) のうち, B_1(a^{(1)}_i) 内にある部分列を (x^{(1)}_m)\subset (x_m) とする。
同様に,いずれかの B_{1/2}(a^{(2)}_j) で, (x^{(1)}_m) を無限個含むものがある。 j が複数ある場合はそのうちの一つを選び, (x^{(1)}_m) のうち, B_{1/2}(a^{(2)}_j) 内にある部分列を (x^{(2)}_m)\subset (x^{(1)}_m) とする。
このように,帰納的に部分列を定める。このとき,点列 (x^{(m)}_m) を考える(対角線論法)と,三角不等式により,
m_1, m_2\ge M\implies d(x^{(m_2)}_{m_2},x^{(m_1)}_{m_1})<\frac{2}{M}
となるため, (x^{(m)}_m) はコーシー列である。 X は完備なので収束する。よって X は点列コンパクトである。
5.\implies 1.について
5.より可分であり,距離空間において可分と第二可算は同値なので, X は第二可算である。また,5.\implies 2.は既に示したので,これと定理1.5より, X はコンパクトである。
証明終