有界とは,簡単に言うと \infty (無限遠)に飛んでいかないということです。
特に,有界数列(点列)・有界関数・有界集合(区間)の3つについて,その定義を考えてみましょう。
有界数列
定義(数列の有界性)
\{a_n \} を数列とする。 \{a_n\} が有界 (bounded) であるとは,ある K > 0 が存在して,
\color{red} |a_n| < K, \quad n \ge 1
が成立することである。
n\ge 1 に依存せずに上からある定数 K で抑えられるということですね。
「|a_n| < K, \,\, n \ge 1 」とは,「任意の n \ge 1 に対して, |a_n| < K 」と同じ意味です。
なお,絶対値さえ定義されれば,数列ではなくもっと一般の点列でも構いません。
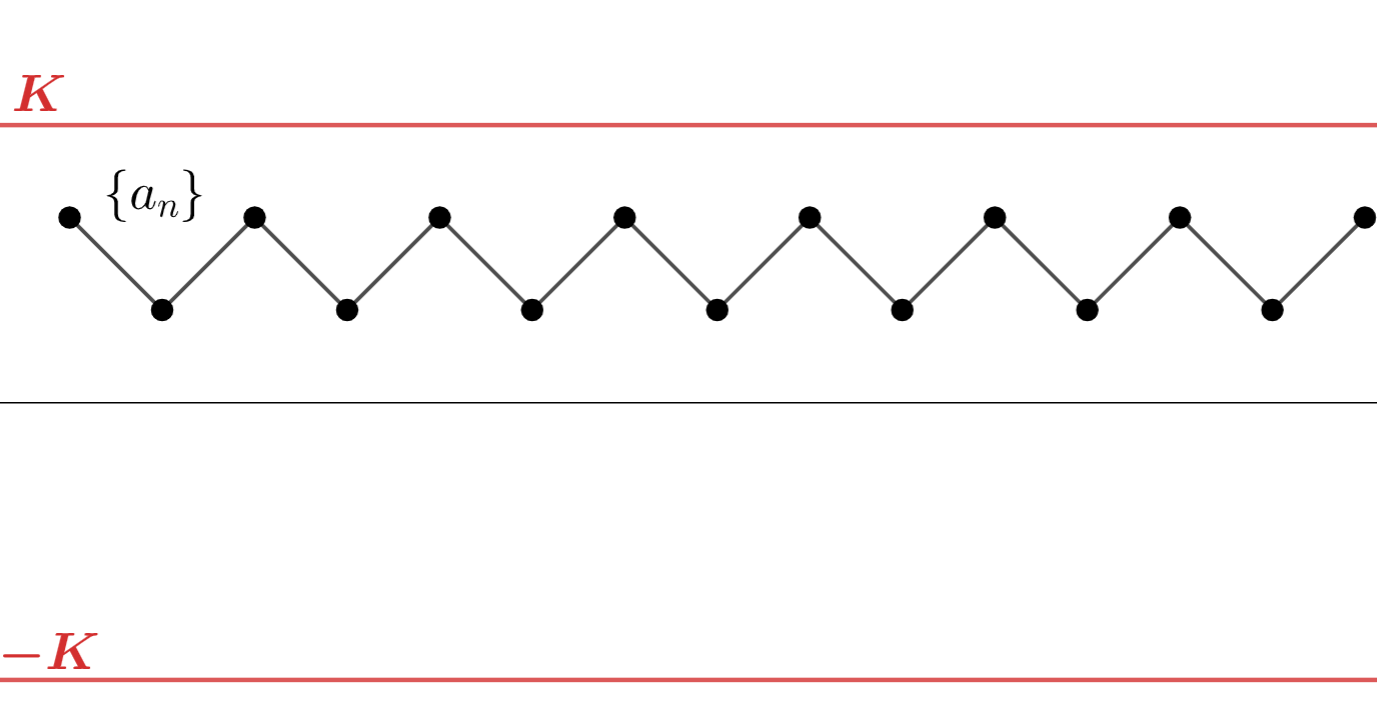
有界な数列のイメージ
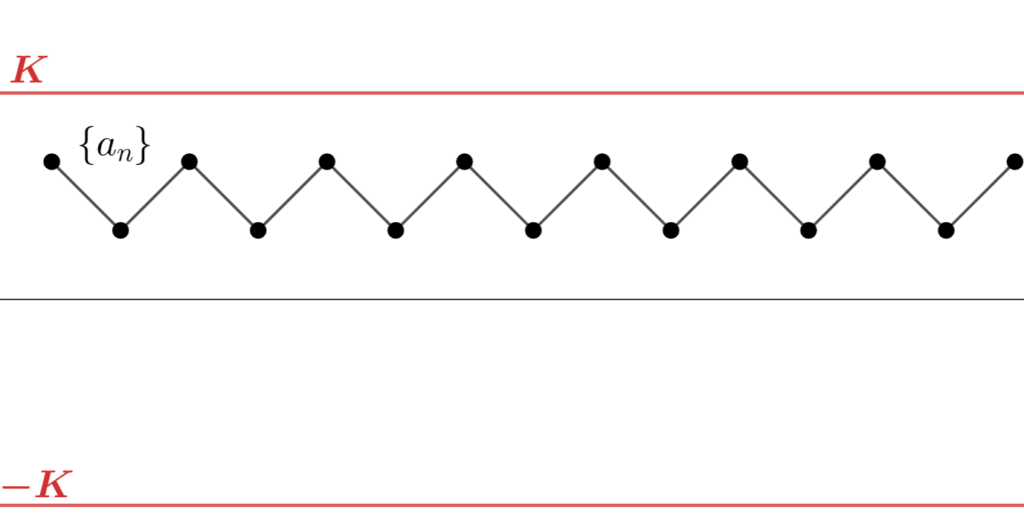
有界でない数列のイメージ
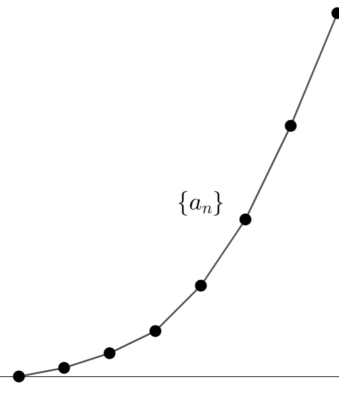
有界でない数列は無限遠に飛んでいきますね。
有界関数
定義(関数の有界性)
f\colon A \to \mathbb{R} \text{ or } \mathbb{C} とする。 f が有界 (bounded) であるとは,ある K > 0 が存在して,
\color{red}|f(x)| < K , \quad x \in A
が成立することである。
x \in A に依存せずに上からある定数 K で抑えられるということですね。
「 |f(x)| < K , \,\, x \in A 」とは,「任意の x \in A に対して |f(x)| < K 」と同じ意味です。
なお, f の終域は,絶対値(に相当するもの)が定義される空間であれば, \mathbb{R} や \mathbb{C} 以外でも,なんでも構いません。
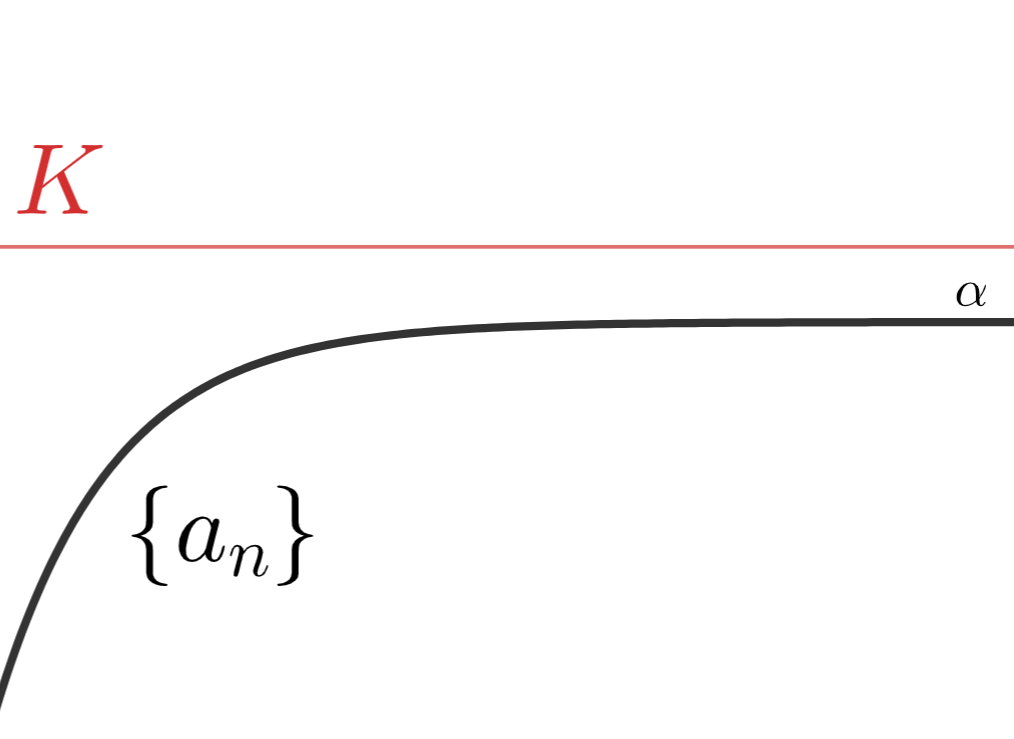
有界な関数のイメージ
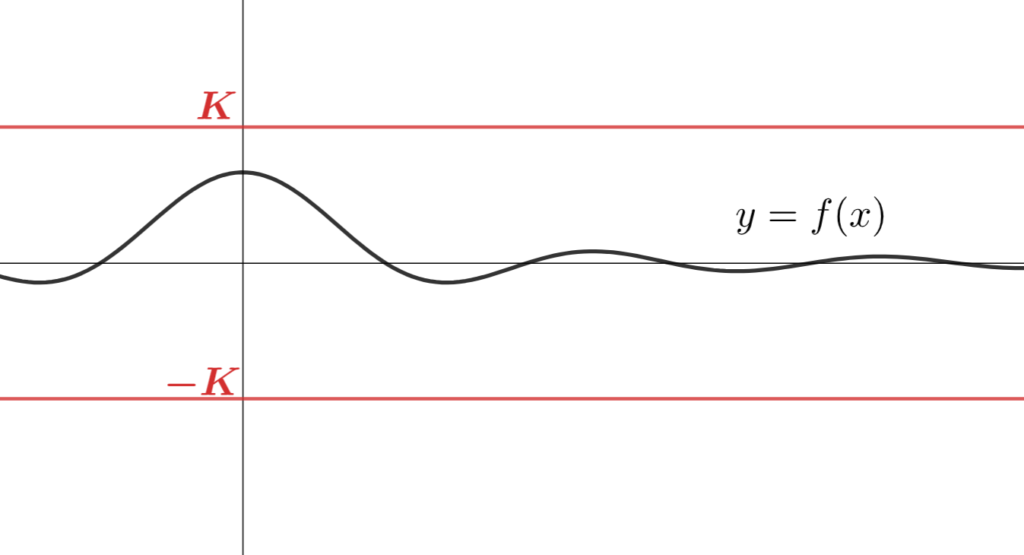
有界でない関数のイメージ
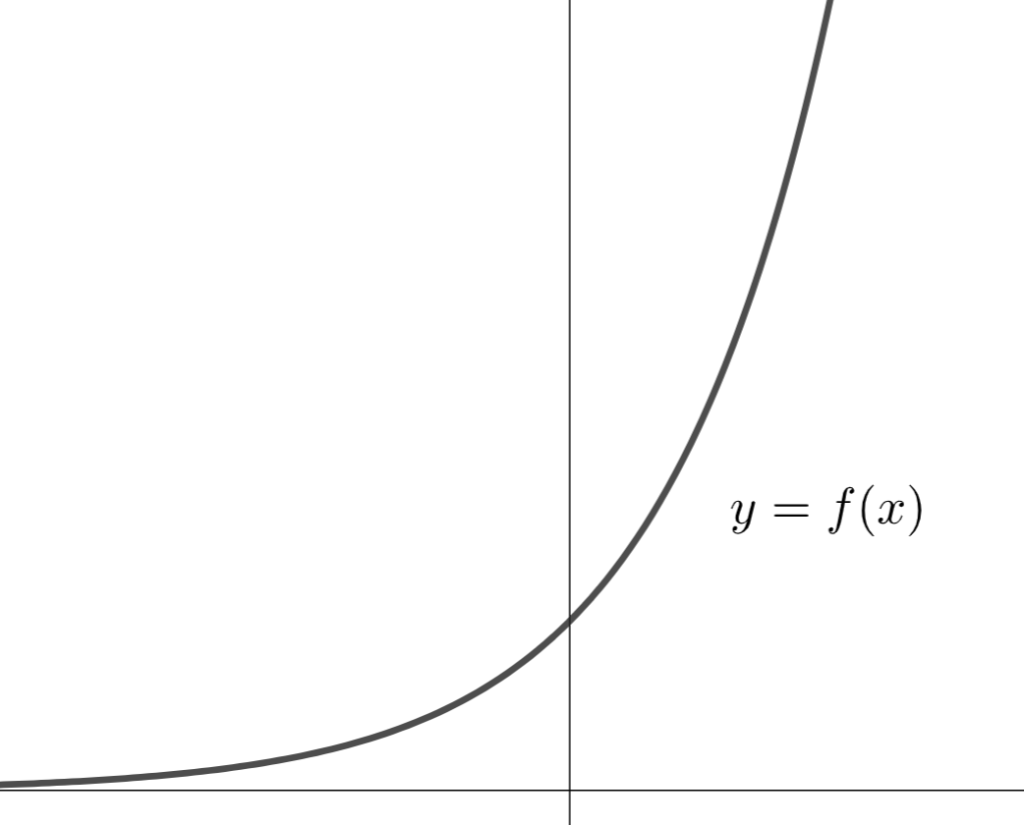
有界でない関数は無限遠点に飛んでいきますね。
有界集合
定義(集合の有界性)
A \in \mathbb{R}^n が有界 (bounded) であるとは,ある R>0 が存在して,
\color{red} A \subset B(0; R)
が成立することである。ただし,
( 0 を中心とする半径 R の n 次元球)と定義する。
「 A \subset B(0; R) 」とは,「任意の x\in A に対して, x \in B(0; R) 」と同じ意味です。
有界な集合のイメージ
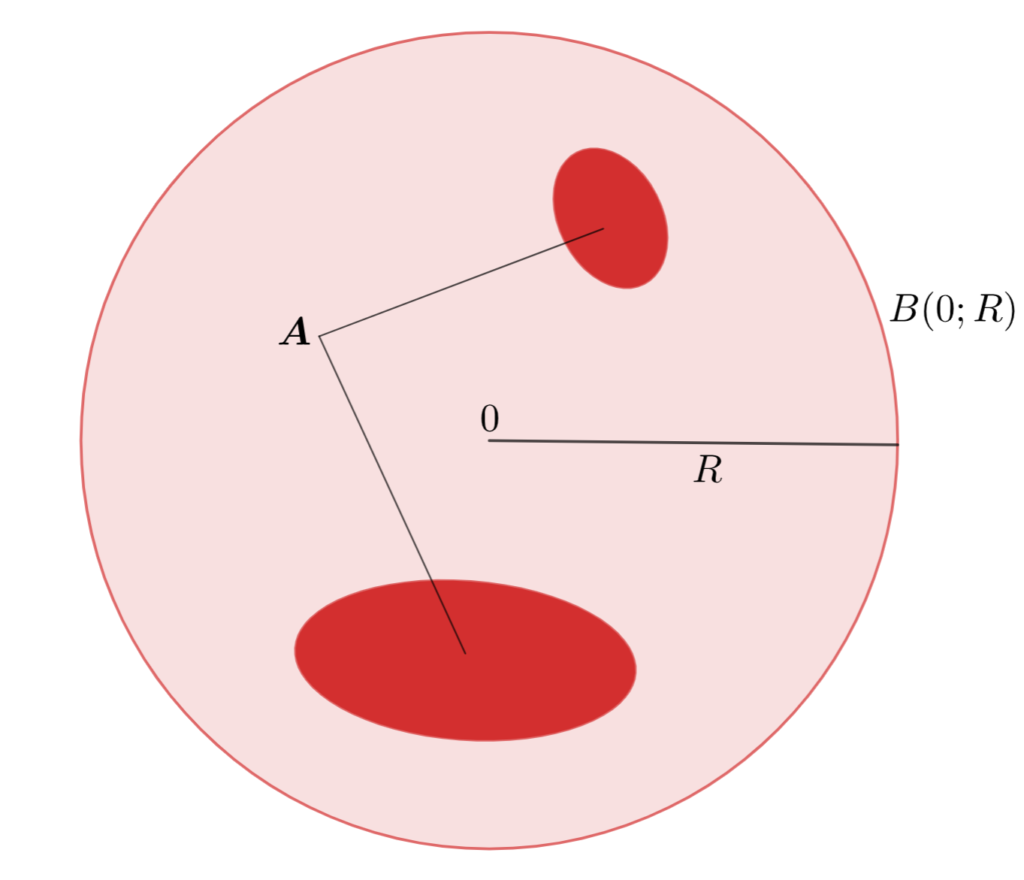
有界でない集合のイメージ

有界でない集合は,集合が無限遠に伸びていますね。
有界区間
\mathbb{R}^n において, n=1 としましょう。このとき,特に \infty < a < b < \infty に対し,区間 \color{red} (a,b), [a, b], [a, b), (a, b] を有界区間といいます。
実際, R=\max\{|a|, |b|\} とすると, [a, b] \subset [-R, R] (他も同様) ですし,「無限遠に飛ばない」と言えますね。
有界に関する話題
有界に関する話題をいくつか列挙しておきましょう。