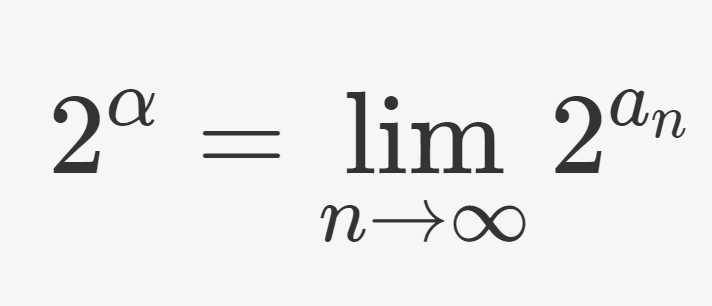数学における well-defined, ill-defined とは,それぞれ「ちゃんと定義できている」,「定義があいまい・無効・無意味である」ことを意味します。専門数学をやっていくにあたっては必須の用語でしょう。この言葉について,具体例も交えながら,分かりやすく紹介しましょう。
【数学】well-defined, ill-definedの定義
定義(well-defined, ill-defined)
「ちゃんと定義できている」,「定義として有効かつ有意義である」ことを well-defined であるといい,「定義できていない・あいまいである」,「定義として無効・無意味である」ことを ill-defined であるという。
define は「定義する」という動詞です。well は「よく」,ill は「悪く」のような雰囲気の意味ですから,well-defined は「ちゃんと定義された」で ill-defined は「定義が悪い」のような意味合いです。この2つは対義語になっています。
また,「ill-defined である」とはいわず「well-defined でない」ということもあります。
なお「定義」の意味は定義・公理・定理・命題・補題・系を完全理解しようを参照してください。
具体例を通して考えた方が,理解しやすいと思うので,実際に具体例を確認していきましょう。
【数学】well-defined, ill-definedの具体例
例1.
\alpha = \lim_{n\to\infty} a_n と定義するとき,この定義は \{a_n\} が収束するなら well-defined であるが,振動するなら ill-defined である。
\lim_{n\to\infty} a_n がちゃんと値として存在するなら,それを \alpha と定義することは「ちゃんと定義できている」わけですが, \lim_{n\to\infty} a_n が定義されないのであれば,それを \alpha とすることは「定義として無効」ですね。
例2(指数関数の定義).
既に非負の有理数 q\in\mathbb{Q}_{\ge 0} に対して, 2^q が定義されているとする。
\alpha \in\mathbb{R}_{\ge 0} とする。 \{a_n\} \subset \mathbb{Q}_{\ge 0} を非負の有理数列とし, a_n\xrightarrow{n\to\infty} \alpha であると仮定したとき,
2^\alpha = \lim_{n\to\infty} 2^{a_n}
と定義する。
この定義は \{a_n\} の取り方に依らず,右辺は同じ値に収束し,さらに \alpha\in \mathbb{Q}_{\ge 0} のときは元の値に一致するから,well-defined である。
2^\alpha を定義するのに, \alpha に収束する有理数列 \{a_n\} を経由して定義していますね。このとき, \{ a_n\} の取り方は複数あり,そのとり方によって収束値が変わってしまうと問題です。そのようなことが起こらないことが分かって初めて定義が正当化されます。
このように,ある定義をするのに,複数の取り方がある別の概念を経由することは多いです。このとき,その「複数の取り方」に依らないことを示して well-defined であるといえることは,専門数学においてとても多いです。
例3.
内角の和が 360^\circ である三角形を「四角型三角形」と定義する。
この定義は,ill-defined である。
内角の和が 360^\circ である三角形はそもそも存在しないため,これに言葉をつけることはナンセンスであり,「定義として無意味」ですね。
well-definedが出現する記事
専門数学においては,well-definedであるかどうかが重要になる場面が多くあります。well-definedが出現する記事は,以下で確認してみてください。