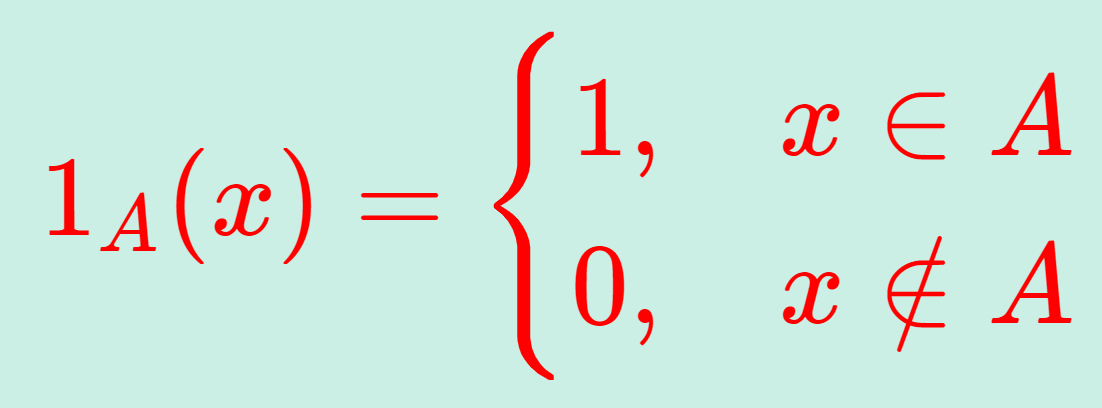大学数学でよく使われる「定義関数(指示関数,特性関数ともいう)」について解説します。その定義自体は難しいものではなく,いわゆる「便利記号」の一つです。
注釈なしで出てくることがあるので,覚えておきましょう。
なお,確率論では,「特性関数」というと,ここでいう「定義関数」とは意味が変わります。今回は確率論の文脈の特性関数を解説しているわけではないので,注意してください。
確率論の特性関数については,いずれ記事にしたいと思います。
それでは解説に移りましょう。
定義関数(指示関数,特性関数)の定義
定義(定義関数,指示関数,特性関数)
集合 A に対し,
\textcolor{red}{1_A (x) = \begin{cases} 1 & x \in A,\\ 0 & x \notin A \end{cases}}
となる関数 1_A を定義関数 (指示関数, indicator function) または特性関数 (characteristic function) という。定義関数は 1_A だけでなく,
などと書かれることが多い( \chi はギリシャ文字「カイ」)。
また, x に依存する命題 P(x) に関して,
\textcolor{red}{1_P(x) = \begin{cases} 1, & \text{if } P(x)\text{ is true,} \\ 0, & \text{if } P(x)\text{ is false} \\ \end{cases} }
として用いる場合もある(trueは真,falseは偽の意味)。
なお本サイトでは,3つの表記のうち, 1_A という表記を一貫して採用します。
定義関数(指示関数,特性関数)の具体例
早速,具体例を確認していきましょう。
例1.(積分)
f\colon \mathbb{R} \to \mathbb{R} を(積分ができる)関数とする。このとき,
\int_{\mathbb{R}} f(x) 1_{[-1, 1]} (x) dx = \int_{-1}^1 f(x) dx
である。
積分区間を制限するのに用いるやり方ですね。
例2.(積分その2)
A \subset \mathbb{R}^2 を”性質の良い”集合(すなわち面積確定集合)とすると, A の面積は
\int_{\mathbb{R}^2} 1_A (x) dx = \int_A dx
として定義される。
大学生が最初に定義関数を見るのが,もしかしたら「面積」や「体積」を積分で定義する場面だったかもしれません。
例3.(場合分け)
A_1, A_2, \ldots, A_n をどの2つも互いに素な(すなわち共通部分をもたない)集合とする。このとき,
f(x) = \begin{cases} a_1 & \text{ if } x \in A_1, \\ a_2 & \text{ if } x \in A_2, \\ \ldots & \ldots \\ a_n& \text{ if } x \in A_n, \\ 0 & \text{otherwise} \end{cases}
となる関数 f は,定義関数を用いると,
とかける。
場合分けにもうまく適用できました。
例4.(場合分けその2)
[x] は, x を超えない最大の整数を表すとすると,
\begin{aligned} [x] &= \sum_{n=-\infty}^\infty n \, 1_{[n, n+1)} (x) \\ &= \sum_{n=-\infty}^\infty n \, 1_{n \le x <n+1}(x) \end{aligned}
となる。
最後の例の最後の書き方は,「集合」を添え字にするのではなく, n \le x < n+1 という「命題」を添え字にしていると思えます。
まとめ
定義関数(指示関数,特性関数)は,大学数学において特に注釈なく出てくることがあります。 1_A, 1\hspace{-2.5mm}1_A, \chi_A のどの表記で出てきても良いように,しっかりと覚えておくようにしましょう。