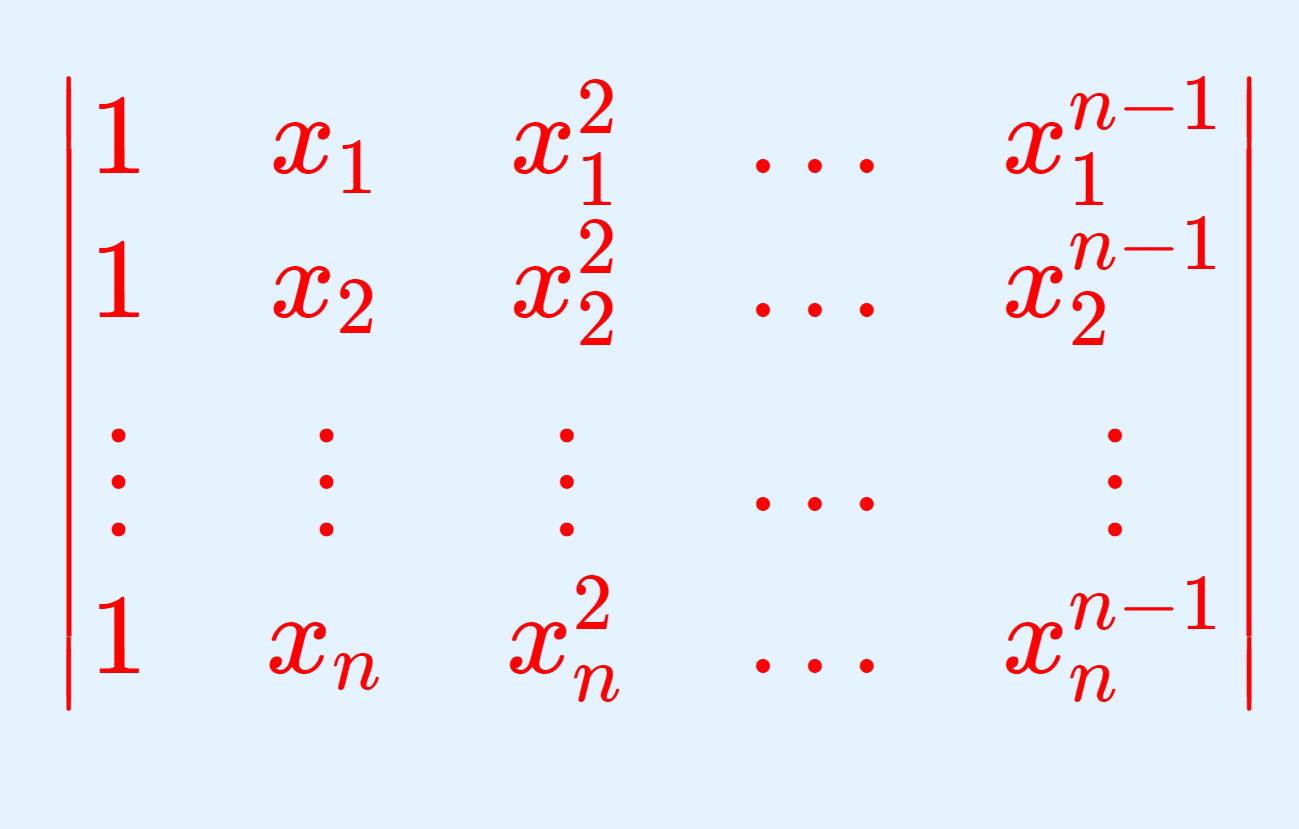ファンデルモンドの行列式 (ヴァンデルモンドの行列式; Vandermonde determinant) といわれる特殊な行列式について紹介し,それを2通りの方法で証明します。
ファンデルモンド行列の定義
定義(ファンデルモンド行列)
以下の n 次正方行列
\color{red} \begin{pmatrix} 1 & x_1 & x_1^2 & \dots &x_1^{n-1} \\ 1 & x_2 & x_2^2 & \dots & x_2^{n-1} \\ \vdots & \vdots & \vdots & \cdots & \vdots \\ 1 & x_n & x_n^2 & \dots & x_n^{n-1} \end{pmatrix}
をファンデルモンド行列 (Vandermonde matrix) という。
なお,上の転置行列である
\color{red} \begin{pmatrix} 1 & 1 & \dots &1\\ x_1 & x_2 & \dots & x_n \\ x_1^2 & x_2^2 & \dots & x_n^2 \\ \vdots & \vdots & \cdots & \vdots \\ x_1^{n-1} & x_2^{n-1} & \dots & x_n^{n-1} \end{pmatrix}をファンデルモンド行列とすることもあります。一般に \det A = \det A^\top であるため(→証明はこちら)どちらで定義しても行列式は一致します。
ファンデルモンドの行列式
ファンデルモンド行列の行列式( \det )をファンデルモンドの行列式 (Vandermonde determinant) といいます。これについて,以下が成り立ちます。
定理(ファンデルモンドの行列式)
\color{red} \begin{vmatrix} 1 & x_1 & x_1^2 & \dots &x_1^{n-1} \\ 1 & x_2 & x_2^2 & \dots & x_2^{n-1} \\ \vdots & \vdots & \vdots & \cdots & \vdots \\ 1 & x_n & x_n^2 & \dots & x_n^{n-1} \end{vmatrix} = \prod_{i<j} (x_j - x_i)
が成立する。
これについて,
- 因数定理を用いた証明
- 帰納法を用いた証明
の2通りで証明しましょう。
因数定理を用いたファンデルモンド行列式の証明
証明
行列式の定義から,求める行列式は 0 + 1 + \dots +(n-1) = n(n-1)/2 次の多項式であることに注意する。
x_i = x_j \, (i < j ) と仮定しよう。このとき,ファンデルモンド行列の第 i, j 行は一致するから,行列式は 0 となる。よって因数定理により行列式は (x_j - x_i) を因数に持つ。
故に,求める行列式は \prod_{i<j} (x_j-x_i) で割り切れる。 \prod_{i<j} (x_j - x_i) は n(n-1)/2 次の式であるから,求める行列式はこれ以外に(定数以外の)因数を持たない。すなわち,求める行列式は
c \prod_{i<j} (x_j-x_i)
の形である。ファンデルモンド行列の対角成分の積である x_2 x_3^2 \dots x_n^{n-1} の係数を両辺で比較することで, c = 1 を得る。
証明終
帰納法を用いたファンデルモンド行列式の証明
証明
行列式(det)の定義と現実的な求め方~計算の手順~に従って,式変形していく(式変形の詳細は後で解説してある)。
\small \begin{aligned} &\begin{vmatrix} 1 & x_1 & x_1^2 & \dots &x_1^{n-1} \\ 1 & x_2 & x_2^2 & \dots & x_2^{n-1} \\ \vdots & \vdots & \vdots & \cdots & \vdots \\ 1 & x_n & x_n^2 & \dots & x_n^{n-1} \end{vmatrix} \\ &= \begin{vmatrix} 1 & x_1 & x_1^2 & \dots &x_1^{n-1} \\ 0 & x_2 - x_1& x_2^2 - x_1^2& \dots & x_2^{n-1} - x_1^{n-1} \\ \vdots & \vdots & \vdots & \cdots & \vdots \\ 0 & x_n - x_1 & x_n^2 - x_1^2& \dots & x_n^{n-1}- x_1^{n-1} \end{vmatrix} \\ &= \begin{vmatrix} x_2 - x_1& x_2^2 - x_1^2& \dots & x_2^{n-1} - x_1^{n-1} \\ \vdots & \vdots & \cdots & \vdots \\ x_n - x_1 & x_n^2 - x_1^2& \dots & x_n^{n-1}- x_1^{n-1} \end{vmatrix} \\ &= \begin{vmatrix} x_2 - x_1& x_2^2 - x_1x_2& \dots & x_2^{n-1} - x_1x_2^{n-2} \\ \vdots & \vdots & \cdots & \vdots \\ x_n - x_1 & x_n^2 - x_1x_n& \dots & x_n^{n-1}- x_1x_n^{n-2} \end{vmatrix} \\ &= \begin{vmatrix} x_2 - x_1& x_2(x_2-x_1)& \dots & x_2^{n-2}(x_2-x_1) \\ \vdots & \vdots & \cdots & \vdots \\ x_n - x_1 & x_n(x_n- x_1)& \dots & x_n^{n-2}(x_n-x_1) \end{vmatrix} \\ &= \prod_{j=2}^n (x_j-x_1) \begin{vmatrix} 1& x_2 & \dots & x_2^{n-2} \\ \vdots & \vdots & \cdots & \vdots \\ 1& x_n& \dots & x_n^{n-2} \end{vmatrix}\end{aligned}ただし,式変形は以下の手順で行った。
- 第 1 行の -1 倍を他の行に加える
- 第 1 列に対して展開する
- 第 k 列の -x_1 倍を第 k+1 列に加える
- 因数をまとめる
- 第 k 行を (x_{k+1} - x_k ) で割る
よって数学的帰納法により,結論が従う。
証明終
有用な行列式の1つですから,覚えておくとよいでしょう。
その他の有用な行列式
一般の行列式の性質については,以下の記事を参照してください。