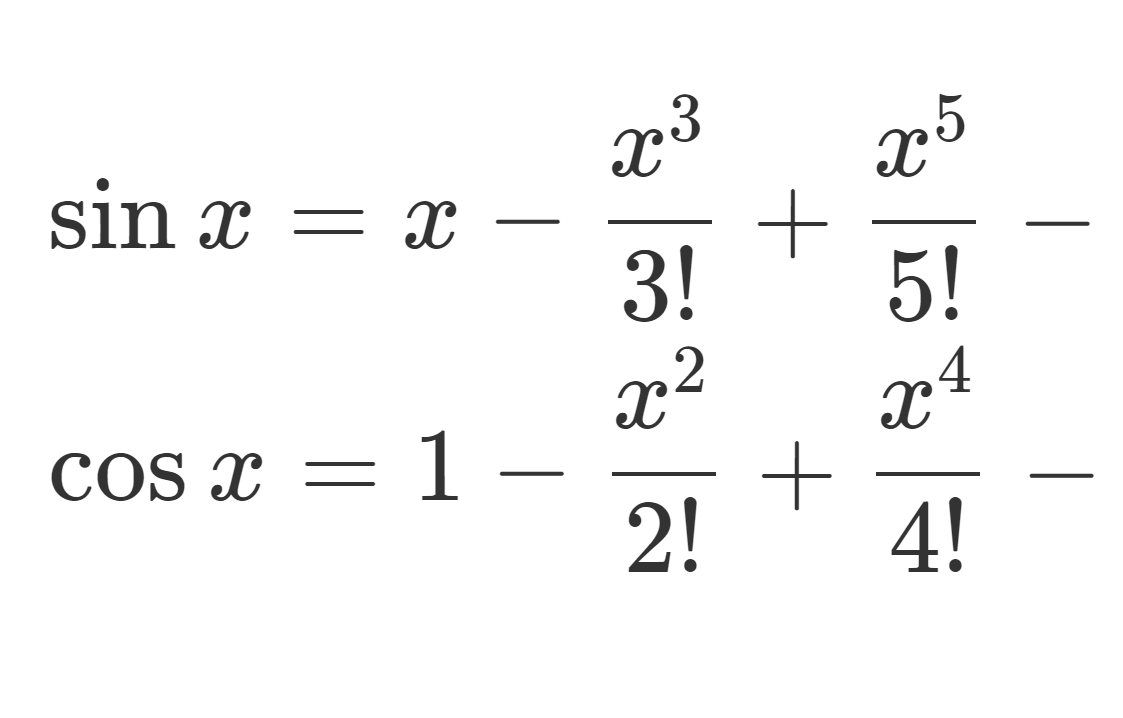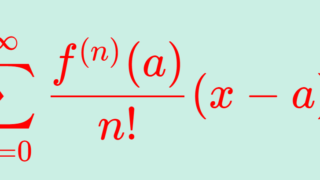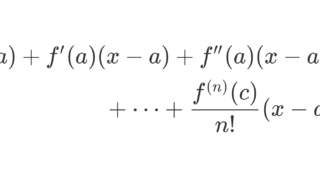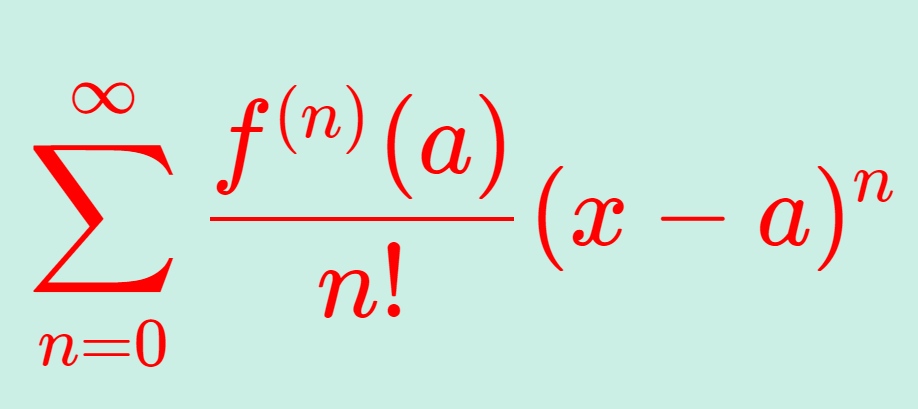サイン・コサインの0でのテイラー展開,すなわちマクローリン展開は
\small \displaystyle \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \dots + (-1)^n \frac{x^{2n+1}}{(2n+1)!} + \cdots, \,\, (|x|<\infty), \\ \cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \dots + (-1)^n \frac{x^{2n}}{(2n)!} + \cdots, \,\, (|x|<\infty).
になります。これの導出について,詳しく確認していきましょう。
三角関数sin,cosのマクローリン展開(0でのテイラー展開)
もう一度,結論を述べましょう。
定理( \sin,\cos のマクローリン展開)
\sin x , \cos x はどちらもマクローリン展開可能であり,
\color{red} \small \displaystyle \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \dots + (-1)^n \frac{x^{2n+1}}{(2n+1)!} + \cdots, \,\, (|x|<\infty), \\ \cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \dots + (-1)^n \frac{x^{2n}}{(2n)!} + \cdots, \,\, (|x|<\infty).
である。特に収束半径はどちらも \infty である。
これの導出について,様々な視点から考察するのが本記事です。
三角関数sin,cosのマクローリン展開の導出
詳しい導出について
- そもそもマクローリン展開とは
- 形式的な導出
- ちゃんとした導出
- オイラーの公式からみた視点
の順に紹介していきましょう。
そもそもマクローリン展開とは
マクローリン展開の厳密な定義を復習しましょう。
定義(マクローリン展開)
f を C^\infty 級関数(すなわち無限回微分可能)とする。 0 の近くで
\small\color{red} \begin{aligned} f(x) ={}& f(0)+ f'(0)x + \frac{f''(0)}{2!}x^2 \\ & \hspace{20pt} + \dots + \frac{f^{(n-1)}(x)}{(n-1)!}x^{n-1} + \textcolor{red}{R_n} \end{aligned}と表したとき, R_n \xrightarrow{n\to\infty} 0 となるならば,
\small \color{red}\begin{aligned} &f(x) = \sum_{n=0}^\infty\frac{ f^{(n)}(0)}{n!} x^n \\ &= f(0) + f'(0)x + \frac{f''(a)}{2!} x^2 + \cdots \end{aligned}
とできる。これを f のマクローリン展開 (Maclaurin expansion) という。
なお,テイラー展開は上において,中心を a に移動させたもの,すなわち x を x-a に置き換え, f^{(k)} (0) を f^{(k)}(a) 置き換えたものになります。
sin,cosのマクローリン展開の形式的な導出
さて,まずは形式的な導出を考えましょう。マクローリン展開の結論の式
\small \begin{aligned} &f(x) = \sum_{n=0}^\infty\frac{ f^{(n)}(0)}{n!} x^n \\ &= f(0) + f'(0)x + \frac{f''(a)}{2!} x^2 + \cdots \end{aligned}に形式的に当てはめることを考えます。今の場合は f(x)= \sin x と f(x) = \cos x ですね。 (\sin x)' = \cos x, (\cos x)' = -\sin x, \sin 0 =0, \cos 0 = 1 であることを思い出すと,
- f(x) = \sin x のとき, f^{(n)}(0) = \begin{cases} 0 & n=2k , \\ (-1)^k & n=2k+1 \end{cases}
- f(x) = \cos x のとき, f^{(n)}(0) =\begin{cases} (-1)^k & n=2k , \\ 0 & n=2k+1 \end{cases}
になることが分かるでしょう。(更に簡単に書くと (\sin x)^{(n)} = \sin(x+n\pi/2), (\cos x)^{(n)} = \cos (x+ n\pi/2) と書けます)このことを用いると,形式的に
\small \begin{aligned} \sin x &= x - \frac{x^3}{3!} + \frac{x^5}{5!} - \dots + (-1)^n \frac{x^{2n+1}}{(2n+1)!} + \cdots\\ \cos x &= 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \dots + (-1)^n \frac{x^{2n}}{(2n)!} + \cdots \end{aligned}
が得られます。ここで
なので,コーシーアダマールの公式を用いると収束半径は \infty だとわかり,上の無限級数の式は |x|<\infty で成立すると求まりますね。
sin,cosのマクローリン展開のちゃんとした導出
上はあくまで形式的な導出でした。本当はマクローリン展開の定義の赤字部分 R_n \xrightarrow{n\to\infty} 0 となるならば,のところをちゃんと確認せねばなりません。 C^\infty 級(無限回微分可能)でも,必ずしもマクローリン展開できるとは限らないのです。
形式的な導出はあくまで結論の式に当てはめただけで,そもそも R_n \xrightarrow{n\to\infty} 0 となるかどうかの確認ができていないわけです。
早速確認していきたいのですが,ここでマクローリンの定理といわれる定理を紹介します。
f は 0 の近くで n 回微分可能であるとする。このとき,
\small \begin{aligned} f(x) ={}&\sum_{k=0}^{n-1} \frac{f^{(k)}(0)}{k!} x^k +R_n\\ ={}& f(0)+ f'(0)x + f''(0)x^2 \\ & \hspace{50pt} + \dots +R_n \end{aligned}
と表すと, \color{red} R_n = \dfrac{f^{(n)}(c)}{n!}x^n となる 0<c<x または x<c< 0 が存在する(ラグランジュの剰余項, c は x, n に依存する)。
R_n 部分の表現を得ることができる定理です。マクローリンの定理とその証明については,以下の記事で解説しています。
これを用いて,確かに R_n \xrightarrow{n\to\infty} 0 となることを確認することで,形式的な導出を正当化しましょう。
R_n \xrightarrow{n\to\infty}0 の証明
上の定理により,剰余項について R_n = \dfrac{f^{(n)}(c)}{n!}x^n となる c が存在する。 f(x) = \sin x, \cos x いずれの場合も |f^{(n)}(c)| \le 1 であるから,
|R_n| \le \frac{|x|^n}{n!} \xrightarrow{n\to\infty} 0
従って, R_n \xrightarrow{n\to\infty} 0 が分かった。
証明終
これにより,形式的な導出が正当化できたわけです。
オイラーの公式からみたsin,cosのマクローリン展開
オイラーの公式からみた視点を与えておきましょう。オイラーの公式とは以下のようなものです。
これを用いると, \cos x = \operatorname{Re}( e^{ix}), \sin x = \operatorname{Im} (e^{ix}) と表されるのが分かります。ここで, e^x のマクローリン展開は
e^x = 1 + x+ \frac{x^2}{2!} + \frac{x^3}{3!} +\cdots
ですから,ここに x の代わりに ix を当てはめると,
を得ることになり,実部・虚部を比較することで,
を得ることができます。
複素数におけるsin,cosをマクローリン展開で定義する
得られたマクローリン展開の式は |x| < \infty 上絶対収束するものでした。これは x は実数に限らず,複素数にしても同じです。このことを用いて,複素数における \sin ,\cos は定義することができます。最後にその定義を述べてみましょう。
定義(複素数における \sin, \cos )
z \in \mathbb{C} に対して,
\color{red} \begin{aligned} \cos z &= 1-\frac{z^2}{2!} + \frac{z^4}{4!}- \frac{z^6}{6!}+ \cdots \\ \sin z &= z-\frac{z^3}{3!} +\frac{z^5}{5!} - \frac{z^7}{7!} + \cdots \end{aligned}
と定義する。
e^z も同様に定義することで,複素数版のオイラーの公式 e^{iz} = \cos z + i \sin z も得ることができます。