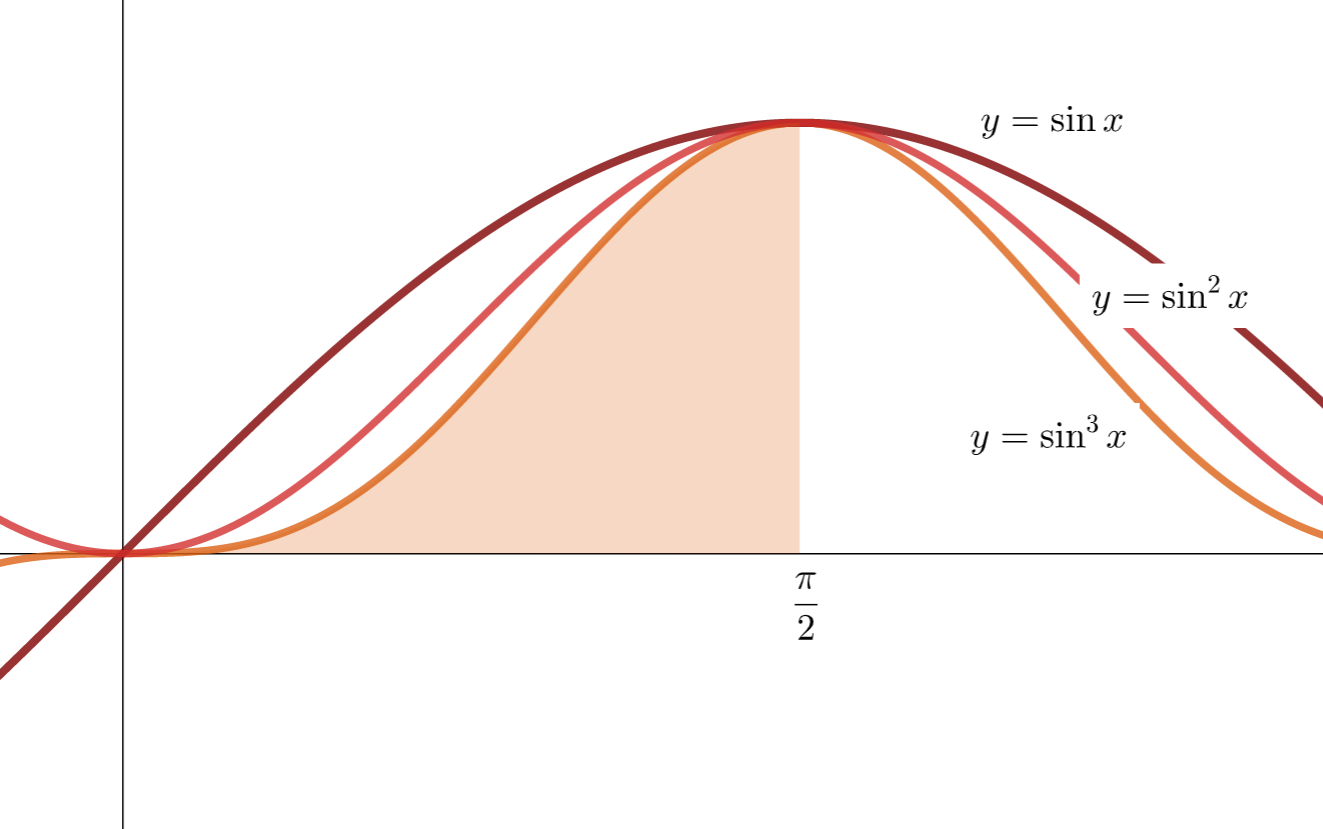
行列単位とは， (i,j) 成分のみが 1 で，それ以外の成分が 0 となる行列を指します。これについて，その定義と積に関する性質を紹介します。
行列単位の定義
定義（行列単位）
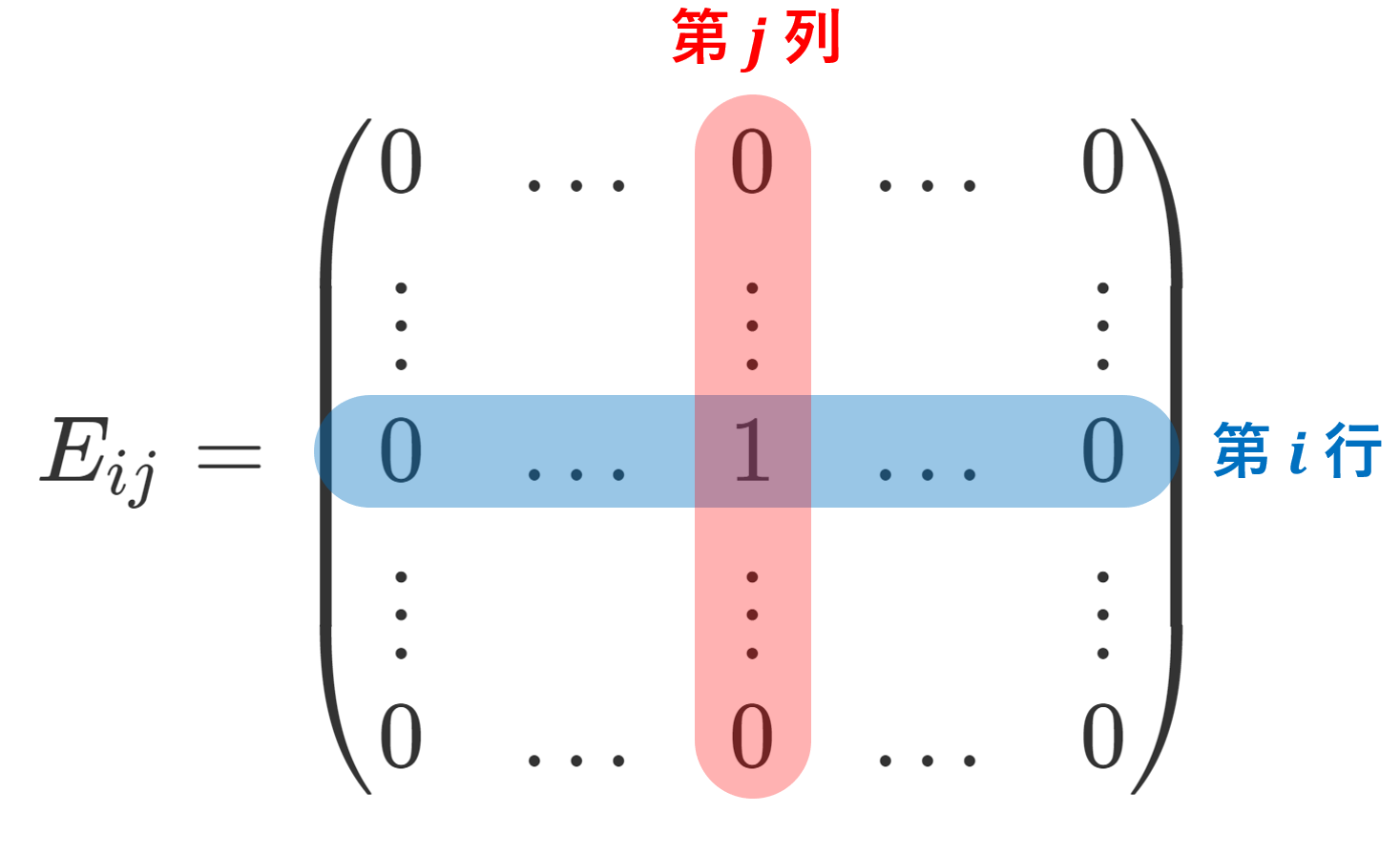
(i,j) 成分のみが 1 でそれ以外の成分が 0 である m\times n 行列 \color{red} E_{ij} を行列単位 (matrix unit)という。
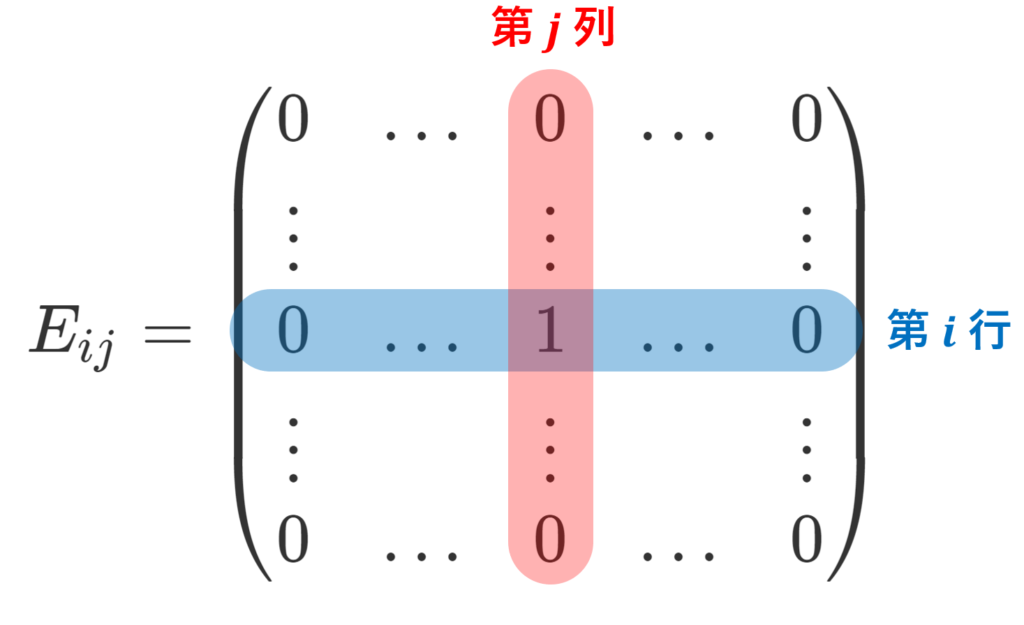
注意ですが，単位行列(identity matrix) とは定義が違います。比較のために，単位行列の定義を述べておきましょう。
n 次正方行列において，(左上から右下への)対角成分のみ 1 でそれ以外は 0 である行列，すなわち
a_{ij} = \begin{cases} 1 & i=j, \\ 0 & i \ne j \end{cases}
となる行列を n 次単位行列 (identity matrix) という。
n 次単位行列は
\begin{pmatrix} 1 & 0 & \ldots & 0 \\ 0 & 1 & \ldots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & 1 \end{pmatrix}
の形である。 n 次単位行列は I, E や I_n, E_n と書かれることが多い。
(i,i), \,\, 1\le i\le n 成分すなわち対角成分が 1 であり，それ以外が 0 である行列が単位行列，単に (i,j ) 成分1つのみが 1 である行列を行列単位というんですね。
単位行列については以下でも解説しています。
行列単位の性質
行列単位と積の性質を述べましょう。
命題（行列単位と積）
1. E_{ij} を m \times n 行列の行列単位， A=(a_{ij}) を n \times l 行列とするとき，
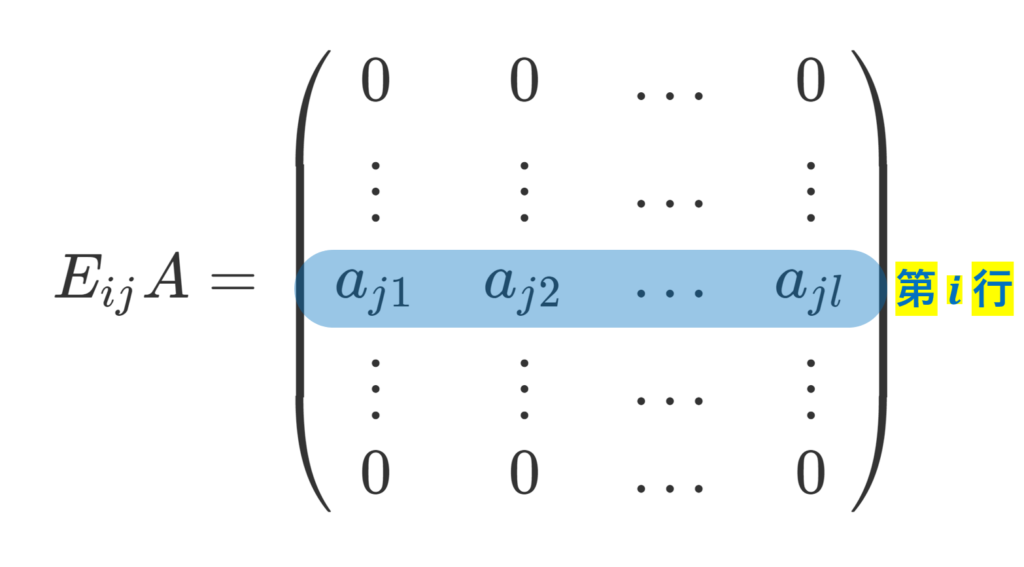
第 i 行となっているのは，第 j 行の誤植ではありませんので注意してください。
2. A=(a_{ij}) を m \times n 行列， E_{ij} を n \times l 行列の行列単位とするとき，
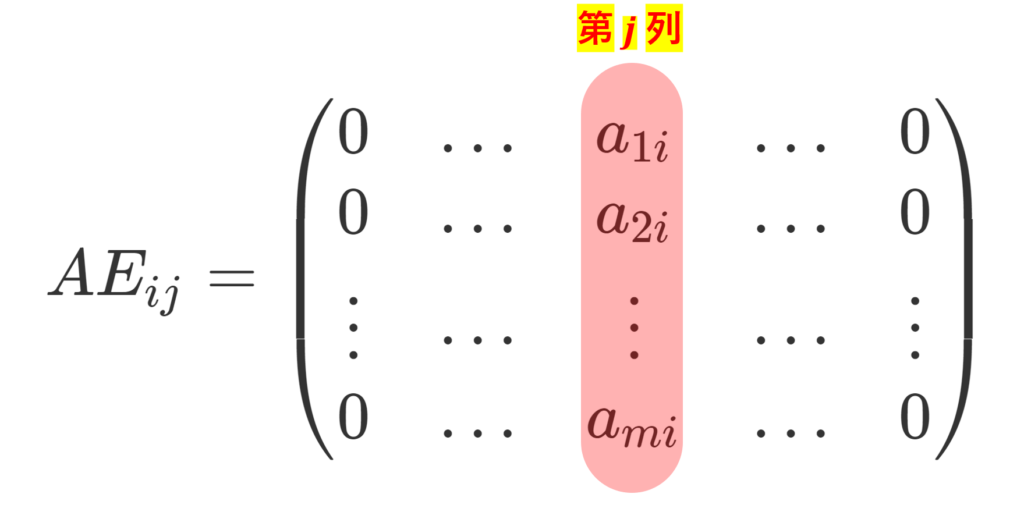
3. E_{ij} を m\times n 行列の行列単位， E_{kl} を n \times p 行列の行列単位とするとき，
E_{ij} E_{kl} = \delta_{jk} E_{il}.
ただし， \delta_{jk} はクロネッカーのデルタであり， \delta_{jk} =\begin{cases} 1 & \text{if }j=k \\ 0 & \text{if } j\ne k\end{cases} と定義される。
行列の積が分かれば，証明は明らかなので省略しましょう。
行列の積を含む，行列の演算については，以下の記事で解説しています。
