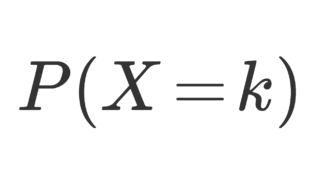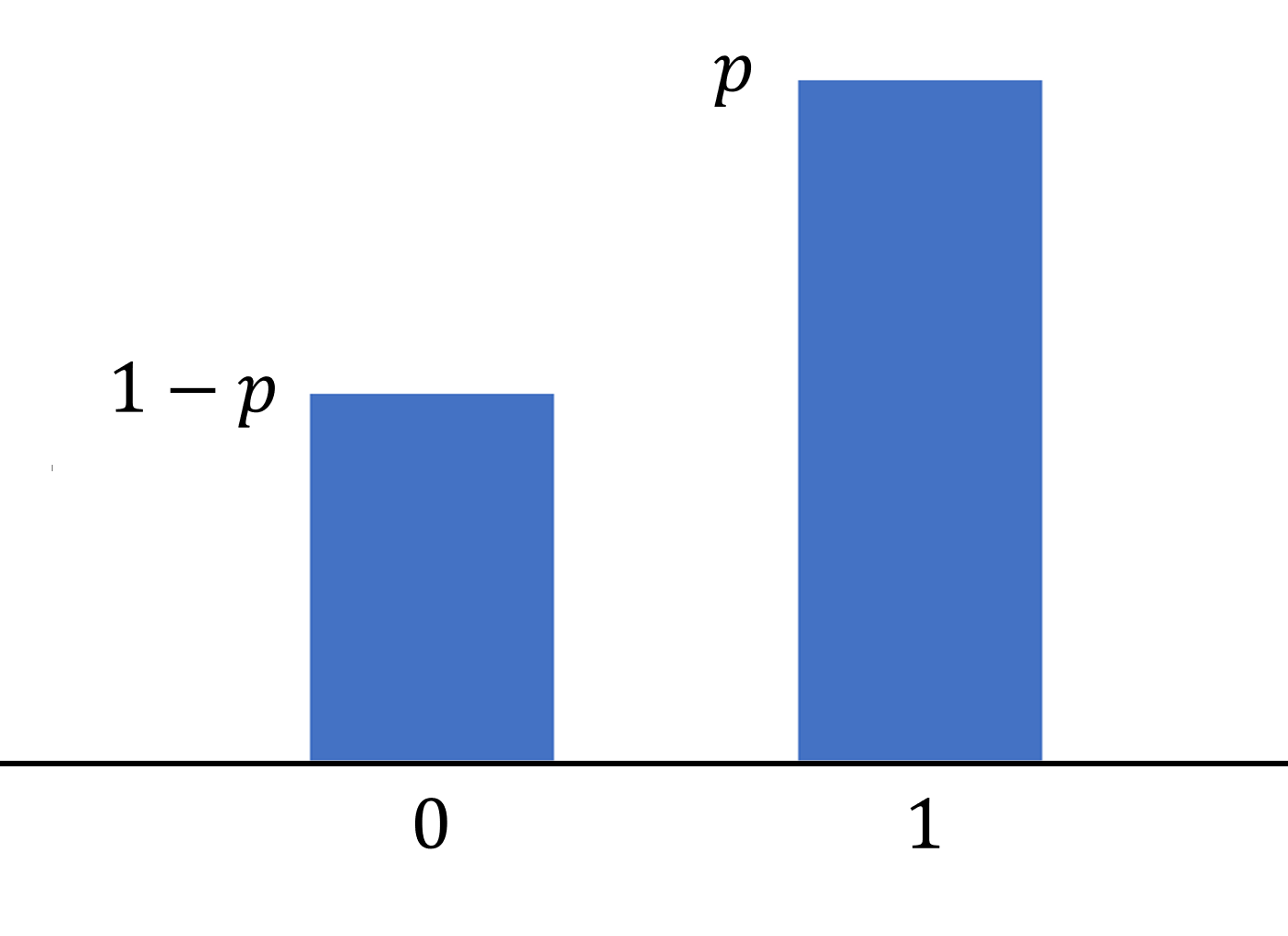一様分布(離散一様分布・連続一様分布)の定義と,その諸性質(平均・分散・標準偏差・積率母関数・特性関数など)を導出付きでまとめます。
一様分布の定義
一様分布には,離散一様分布と連続一様分布があります。まずはそれぞれの定義を確認していきましょう。
離散一様分布
定義(離散一様分布)
確率変数 X が 1,2,3,\dots, n 上離散一様分布 (discrete uniform distribution) に従うとは,
\color{red}P(X=k) = \frac{1}{n}\quad(1\le k \le n)
となることである。
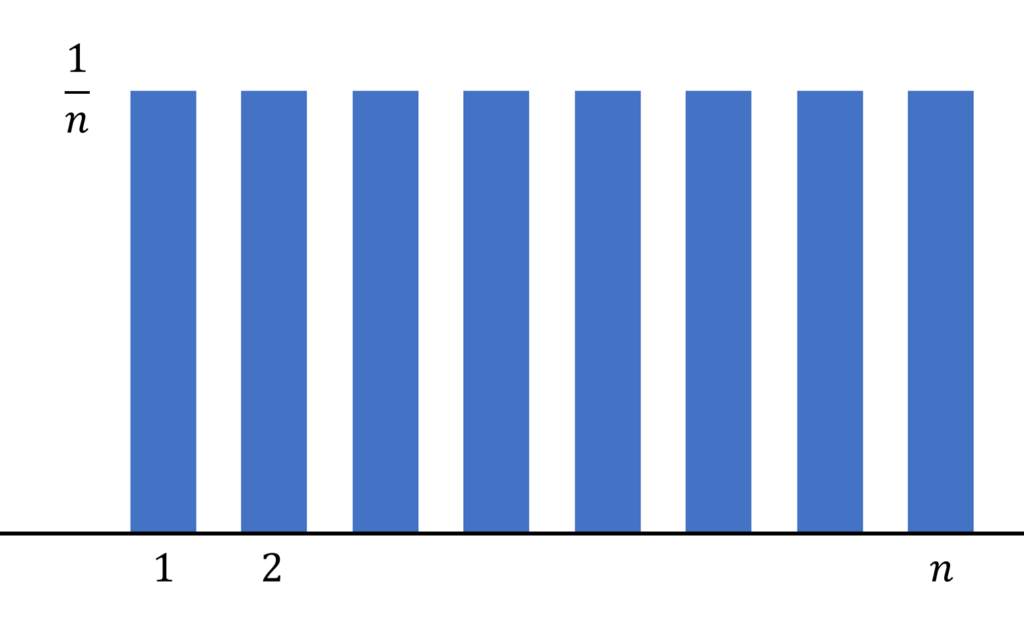
X=1,2,3,\dots, n となる確率が等しいということですね。
たとえば,サイコロの出目 X は P(X=1) = P(X=2) = \dots = P(X=6) =1/6 と考えられることから, 1,2,3,\dots, 6 上の離散一様分布に従っていると言えますね。
なお,整数 m<n に対し, k=m, m+1, \dots, n 上の離散一様分布も考えることができますが,今回は省略します。
連続一様分布(1次元)
定義(連続一様分布)
確率変数 X が [a,b] 上連続一様分布 (continuous uniform distribution) に従うとは,
\color{red} P(X\in A) = \int_{A\cap[a,b]} \frac{dx}{b-a}
となることである。このとき,確率密度関数は
となる。
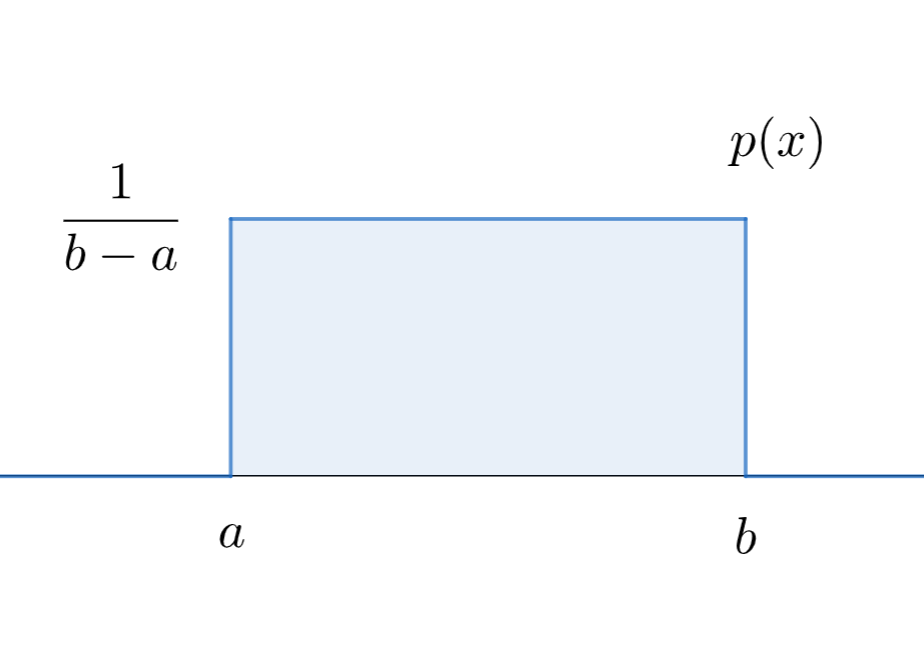
[a,b] という「連続的」な空間において,各集合に属する確率が「一様」である,ということですね。たとえば,区間 [c,d] \subset [a,b] に対し,
P(X\in [c,d]) = \frac{d-c}{b-a}
になります。
確率密度関数が 1/(b-a) \,\,(a\le x\le b) になるのは,積分して 1 にならないといけないからです。 P(X\in [a,b]) = 1 ですからね。
たとえば,ある区間に,ものを無作為に落としたとき,その区間のどこに落ちるかは,連続一様分布に従っていると言えますね。
一様分布の諸性質まとめ
まず最初に,今回考える諸性質を全て列挙しておきましょう。
| 離散一様分布 | 連続一様分布 | |
|---|---|---|
| 定義 | 1,2,\dots, n 上の離散一様分布 | [a,b] 上の連続一様分布 |
| 確率 | P(X=k) = \frac{1}{n}\\ (k=1,2,\dots,n) | \begin{aligned}&P(X\in A) \\&=\int_{A \cap [a,b]} \frac{dx}{b-a} \end{aligned} |
| 確率分布の型 | 離散型 | 連続型 |
| 確率密度関数 p(x) | なし | \begin{cases} \frac{1}{b-a} & a\le x\le b, \\ 0 & \text{otherwise} \end{cases} |
| 累積分布関数 F(x) = P(X\le x) | \begin{cases} 0 & x \le 1, \\ \frac{\lfloor x\rfloor}{n} & 1 \le x \le n , \\ 1 & n\le x \end{cases} | \begin{cases} 0 & x\le a, \\ \frac{x-a}{b-a} & a\le x\le b, \\ 1 & b\le x \end{cases} |
| 平均(期待値) E[X] | \frac{n+1}{2} | \frac{a+b}{2} |
| 分散 V(X) | \frac{n^2-1}{12} | \frac{(b-a)^2}{12} |
| 標準偏差 \sqrt{V(X)} | \frac{1}{2}\sqrt{\frac{n^2-1}{3}} | \frac{b-a}{2\sqrt{3}} |
| 積率母関数 E[e^{tX}] | \frac{e^t-e^{t(n+1)}}{n(1-e^t)} | \frac{e^{tb}-e^{ta}}{(b-a)t} |
| 特性関数 E[e^{it X}] | \frac{e^{it}-e^{it(n+1)}}{n(1-e^{it})} | \frac{e^{itb}-e^{ita}}{i(b-a)t} |
これらの,特に累積分布関数以降ついて,順番に確認していきましょう。
離散一様分布の諸性質
まずは,離散一様分布の性質から確認していきましょう。
離散一様分布の累積分布関数
離散一様分布の累積分布関数(分布関数)は
\color{red} F(x) = P(X\le x ) = \begin{cases} 0 & x \le 1, \\ \lfloor x\rfloor/n & 1 \le x \le n , \\ 1 &n \le x \end{cases}
になります。ここで, \lfloor x\rfloor は床関数(ガウス記号)を表します。グラフを描くと以下のようになります。
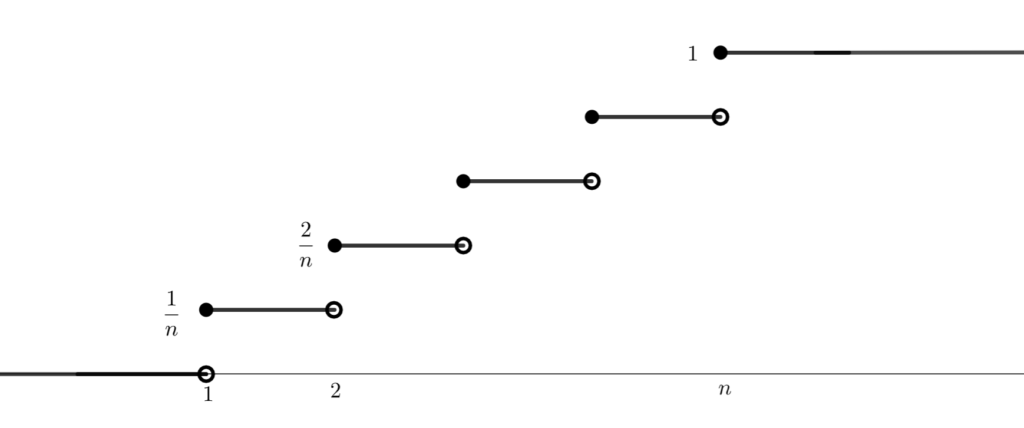
離散一様分布の平均(期待値)
離散一様分布の平均は
\color{red} E[X] = \frac{n+1}{2} になります。
実際,
と計算されるからです。
離散一様分布の分散
離散一様分布の分散は
\color{red} V(X) = \frac{n^2-1}{12}
になります。実際,
と計算されるからです。
離散一様分布の標準偏差
離散一様分布の標準偏差は,分散のルート \sqrt{V(X)} ですから,
\color{red}\sqrt{V(X)} = \frac{1}{2}\sqrt{\frac{n^2-1}{3}}
と求めることができます。
離散一様分布の積率母関数(モーメント母関数)
離散一様分布の積率母関数(モーメント母関数)は,
\color{red} E[e^{tX}] = \frac{e^t-e^{t(n+1)}}{n(1-e^t)}
となります。実際,等比数列の和の公式を用いて,
と計算されるからです。
離散一様分布の特性関数
離散一様分布の特性関数は,
\color{red} E[e^{itX}] =\frac{e^{it}-e^{it(n+1)}}{n(1-e^{it})}
となります。実際,等比数列の和の公式を用いて,
と計算されるからです。
連続一様分布の諸性質
続いて,連続一様分布の性質を確認していきましょう。
連続一様分布の累積分布関数
連続一様分布の累積分布関数(分布関数)は,
\color{red} F(x) = P(X \in (-\infty, x]) = \begin{cases} 0 & x\le a, \\ \frac{x-a}{b-a} & a\le x\le b, \\ 1 & b\le x \end{cases}
になります。実際,
と計算されるからです。グラフを描くと以下のようになります。
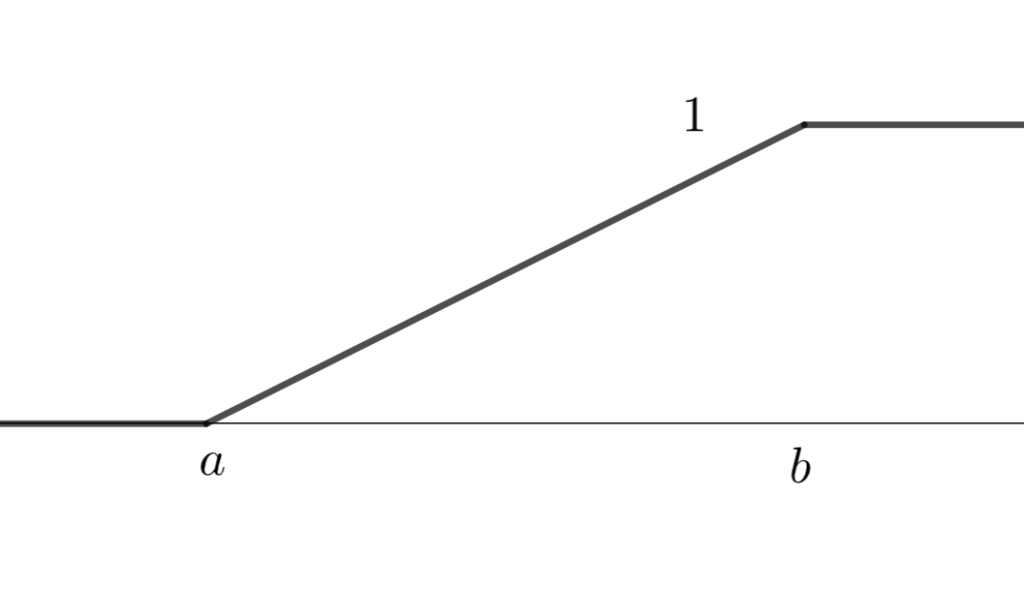
連続一様分布の平均(期待値)
連続一様分布の平均は
\color{red}E[X]= \frac{a+b}{2}
になります。実際,
と計算されるからです。
連続一様分布の分散
連続一様分布の分散は
\color{red} V(X) = \frac{(b-a)^2}{12}
になります。実際,2次モーメントについて
であるため, V(X) = E[X^2] - E[X]^2 = \dfrac{(b-a)^2}{12} となるからです。
連続一様分布の標準偏差
連続一様分布の標準偏差は,分散のルート \sqrt{V(X)} ですから,
\color{red}\sqrt{V(X)} =\frac{b-a}{2\sqrt{3}}
と求めることができます。
連続一様分布の積率母関数(モーメント母関数)
連続一様分布の積率母関数(モーメント母関数)は
\color{red}E[e^{tX}]=\frac{e^{tb}-e^{ta}}{(b-a)t}
となります。実際,
と計算されるからです。
連続一様分布の特性関数
連続一様分布の特性関数は,
\color{red} E[e^{it X}]=\frac{e^{itb}-e^{ita}}{i(b-a)t}
となります。実際,
と計算されるからです。
おわりに
一様分布は最も基本的な分布とも言えますから,しっかりと身につけましょう。