カントール集合の定義と性質3つの証明

カントール集合とは，フラクタルと呼ばれる図形の1つで，連続体濃度を持つにもかかわらず，ルベーグ測度が $0$ となる集合として有名です。

カントール集合について，その定義と性質3つとその証明を行いましょう。

カントール集合の定義
カントール集合の性質3つ
関連する記事

カントール集合の定義

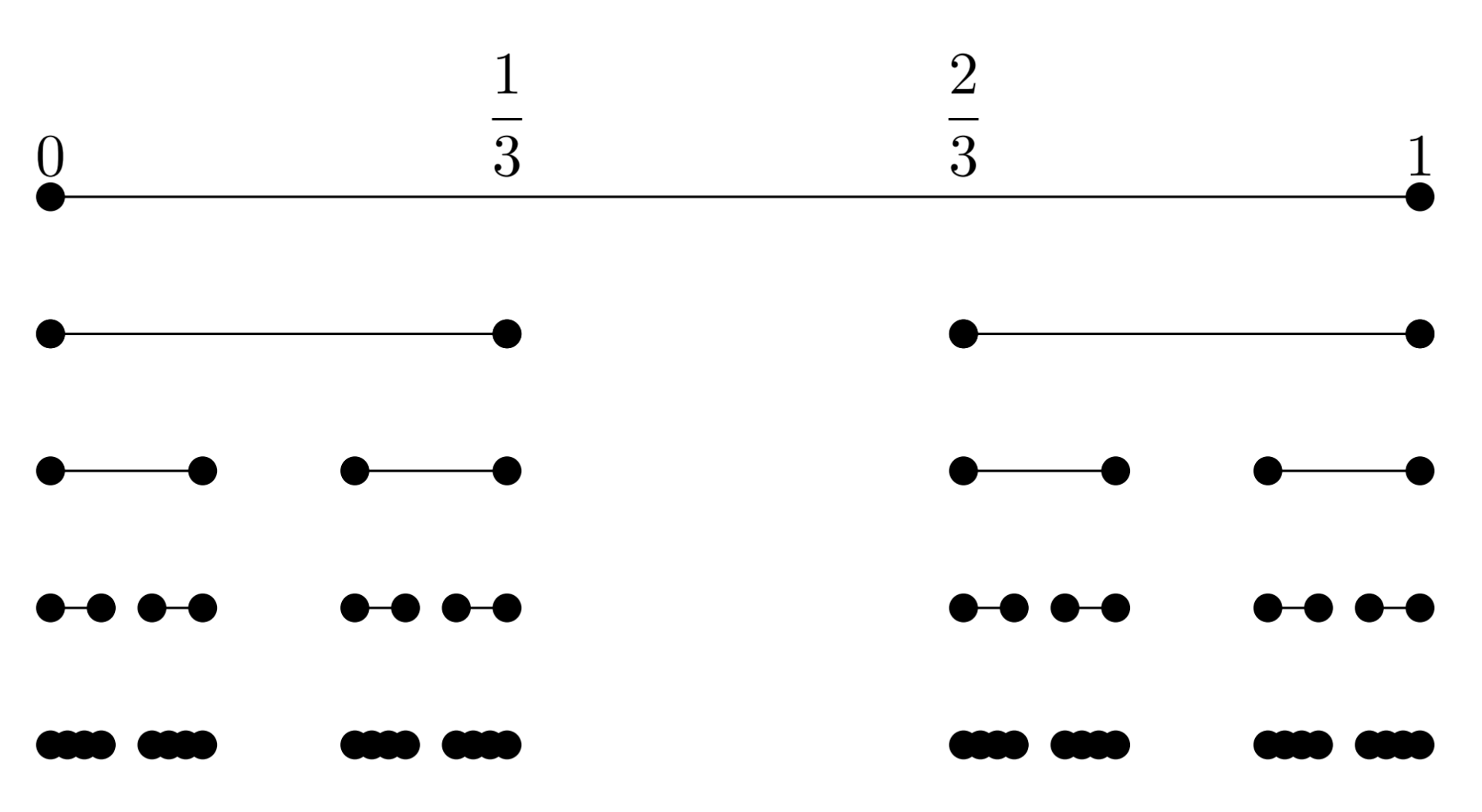
まず， $[0,1]$ 区間を3等分し，間の区間 $\left(\dfrac{1}{3}, \dfrac{2}{3}\right)$ をくり抜くことを考えましょう。

残った2つの閉区間 $\Bigl[0,\cfrac{1}{3}\Bigr]\cup \Bigl[\cfrac{2}{3},1\Bigr]$ をそれぞれ3等分し，間の区間 $\left(\dfrac{1}{9},\dfrac{2}{9}\right), \left(\dfrac{7}{9}, \dfrac{8}{9}\right)$ をくり抜きましょう。

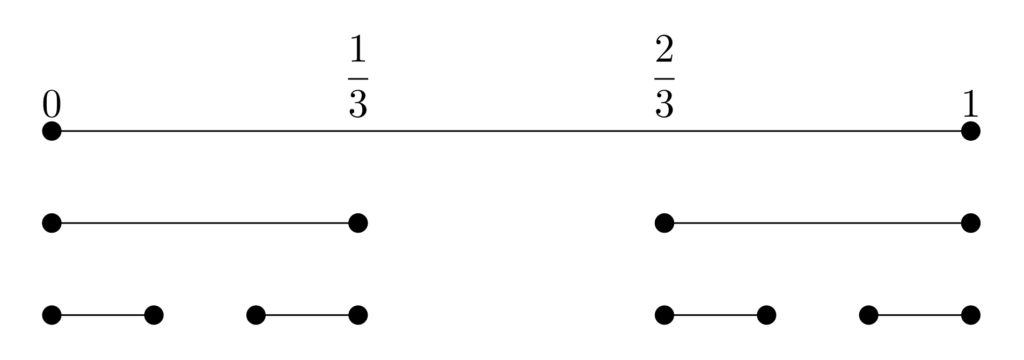
同様の操作を再び各閉区間で繰り返し，この操作を無限回行って得られるのが，カントール集合です。(下の図は，くり抜きを4回繰り返したものです)

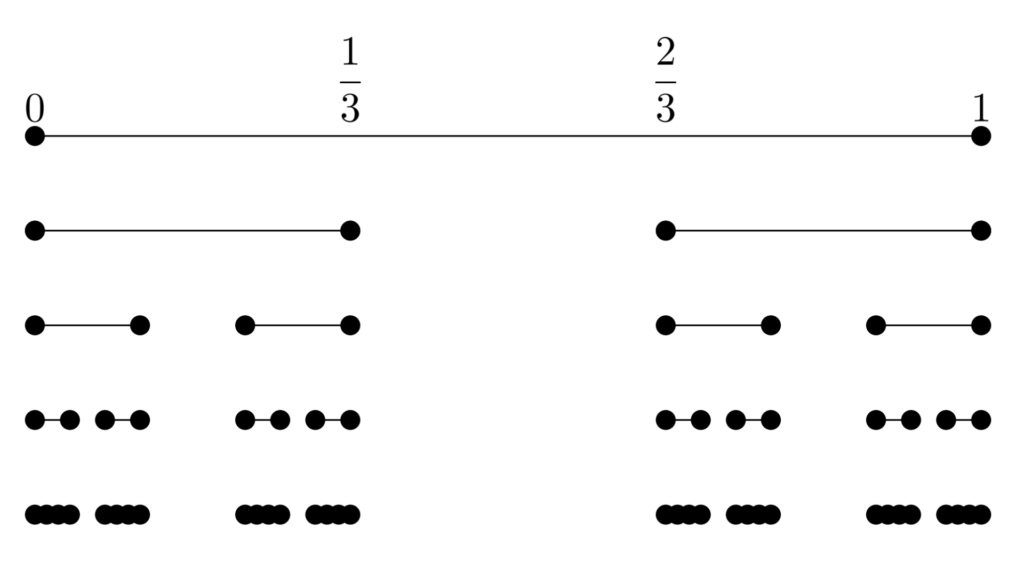
定義を述べましょう。

定義（カントール集合）

線分 $[0,1]$ を三等分し，間をくり抜く作業を無限回繰り返したときに残る集合

\color{red}\mathscr{C}= [0,1]\setminus \bigcup_{n=1}^\infty \bigcup_{k=0}^{3^{n-1}-1} \left( \frac{3k+1}{3^n},\frac{3k+2}{3^n}\right)

をカントール集合 (Cantor set) という。

$[0,1]$ から $\left( \dfrac{3k+1}{3^n},\dfrac{3k+2}{3^n}\right)$ を除く形で定義しましたが，これは， $\left(\dfrac{1}{3}, \dfrac{2}{3}\right)$ をくり抜き，次に $\left(\dfrac{1}{9},\dfrac{2}{9}\right), \left(\dfrac{4}{9}, \dfrac{5}{9}\right), \left(\dfrac{7}{9},\dfrac{8}{9}\right)$ をくり抜き…という形になっており，実際は既に切り抜いているため切り抜かなくてもよい $\left(\dfrac{4}{9}, \dfrac{5}{9}\right)$ も混ざっています。

カントール集合は，フラクタル図形と呼ばれる図形の1つで，自己相似性をもちます。「自己相似性」とは，ざっくりいうと，拡大しても同じような様相を表すことです。

また，カントール集合はカントールの三進集合ともいいます。カントール集合に属する数字を三進数

0.x_1x_2x_3\dots_{(3)}= \sum_{n=1}^\infty \frac{x_n}{3^n}

で表すと， $0.1_{(3)}=0.02222\dots_{(3)}$ などとすることで，任意の桁に $1$ が登場しないようにできます。よって，カントール集合とは，三進展開したときに，どの桁にも $1$ が登場しないものの集まりである，ということができます。具体的には，

\color{red} \mathscr{C}=\left\{\sum_{n=1}^\infty\frac{2a_n}{3^n}\middle| a_n =0,1\right\}

と表せます。

カントール集合の性質3つ

ここからは，カントール集合の性質3つを紹介し，それを証明していきましょう。

定理（カントール集合の性質）

カントール集合は閉集合である。特に，コンパクトである。
カントール集合は連続体濃度( $\mathbb{R}$ と同じ濃度)を持つ。
カントール集合はルベーグ零集合，すなわちルベーグ測度 $0$ の集合である。

それぞれ証明しましょう。以下の証明では，

J_{n}= \bigcup_{k=0}^{3^{n-1}-1}\left( \frac{3k+1}{3^n},\frac{3k+2}{3^n}\right), \; J= \bigcup_{n=1}^\infty J_{n}

とし，カントール集合は $\mathscr{C}= [0,1]\setminus J$ とかくことにします。

1. カントール集合は閉集合である

証明

$J$ は開区間の和より開集合であり，カントール集合は $\mathscr{C}=[0,1]\setminus J$ より，閉集合である。

証明終

2. カントール集合は連続体濃度を持つ

証明

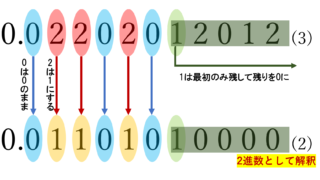
$[0,1]$ 上の二進展開と， $[0,1]$ 上の三進展開で各桁 $0,2$ のみが現れるものとの間には，各桁 $0\to 0, \; 1\to 2$ とするような単射が定まる。ただし， $2$ 進展開については $0.0\dots 0111\dots$ のような，最後に $1$ のみが続くものは考えず，これは $0.0\dots 1000\dots$ として処理するものとする。

これと $\mathscr{C}\subset[0,1]$ であることから，濃度について， $|[0,1]|\le |\mathscr{C}|\le |[0,1]|$ となるため，カントール集合は $[0,1]$ と同じ濃度，すなわち連続体濃度である。

証明終

単射を作る際に述べた但し書きに注意してください。

二進展開については， $0.0\dots 0111\dots = 0.0\dots 1000\dots$ ですが，これらを各桁 $0\to 0, \;1\to 2$ でうつしたものは $0.0\dots 0222\dots \ne 0.0\dots 2000\dots$ ですから，どちらで処理するかちゃんと明示しておかないと写像が well-defined (ちゃんと正しく定義されている状態)でなくなってしまいます。

なお，これが理由で，ここで構成した写像は全単射ではありません。三進展開で $0.0\dots 2000\dots$ に対応する二進展開の元はあっても， $0.0\dots 0222\dots$ に対応する二進展開の元がないからです。なお，この構成はカントール関数 (Cantor function) の構成にも使われます(→カントール関数のさまざまな定義とその重要な性質5つ)。