 線形代数学
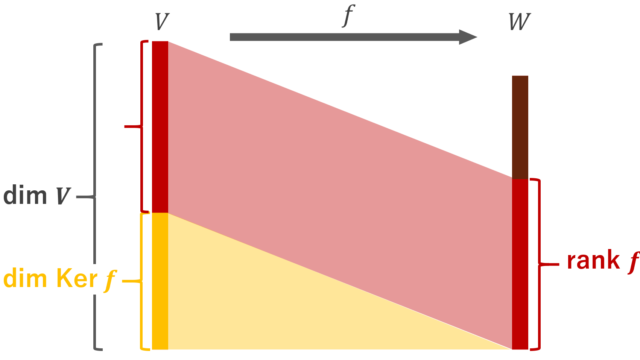
線形代数学 線形写像の次元定理dim V = rank f + dim ker fの証明
線形写像における次元の等式 dim V = rank f + dim Ker f (= dim Im f + dim Ker f) について証明し,そのことから従う定理として,線形写像の全射・単射性とrankとの関係を述べましょう。
 線形代数学
線形代数学  線形代数学
線形代数学  線形代数学
線形代数学  線形代数学
線形代数学  線形代数学
線形代数学 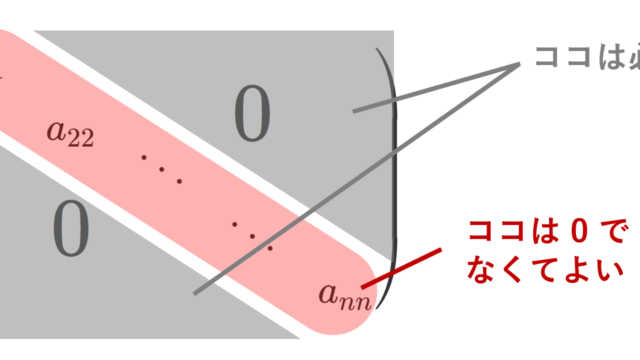 線形代数学
線形代数学 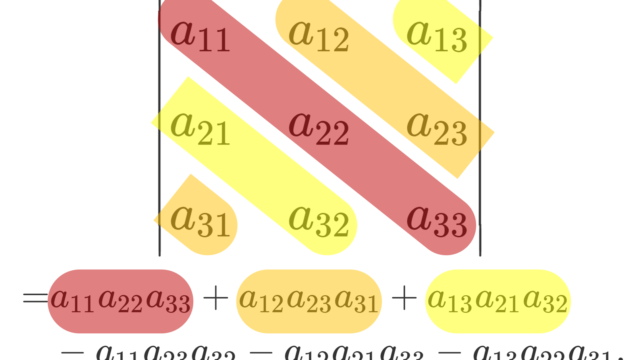 線形代数学
線形代数学 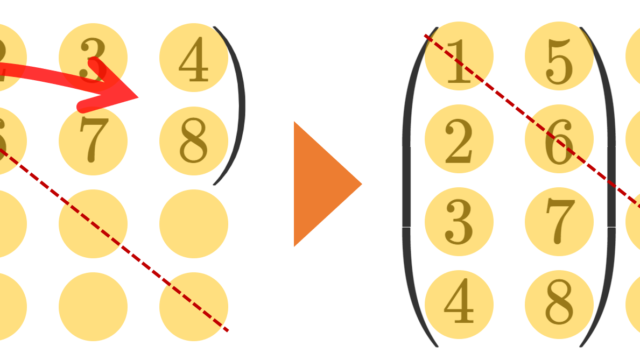 線形代数学
線形代数学 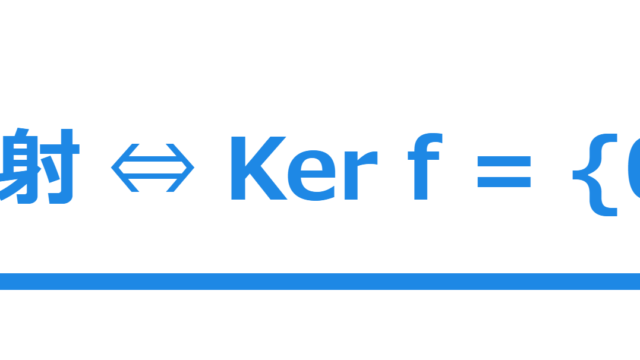 線形代数学
線形代数学  線形代数学
線形代数学