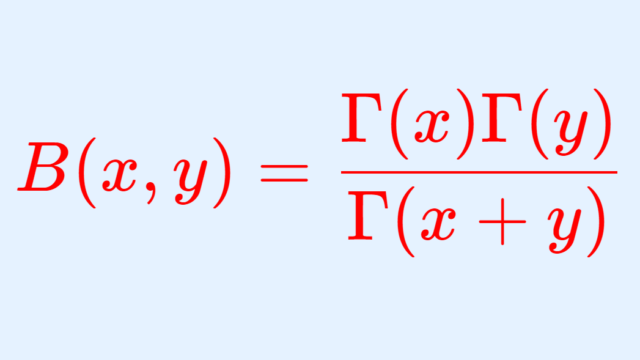 微分積分学(大学)
微分積分学(大学) ガンマ関数とベータ関数の関係式とその証明
ガンマ関数とベータ関数の間には,B(x,y) = Γ(x)Γ(y)/Γ(x+y) という関係式があります。この関係式について,その導出の証明を行いましょう。
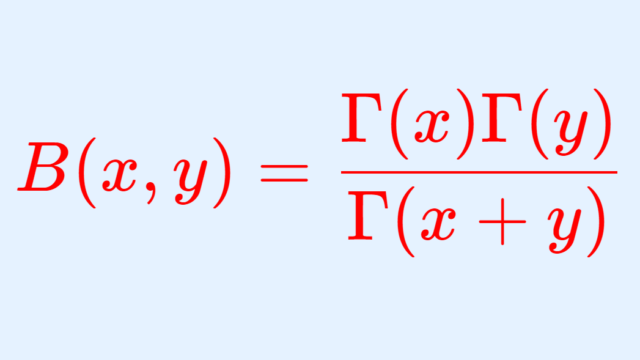 微分積分学(大学)
微分積分学(大学) 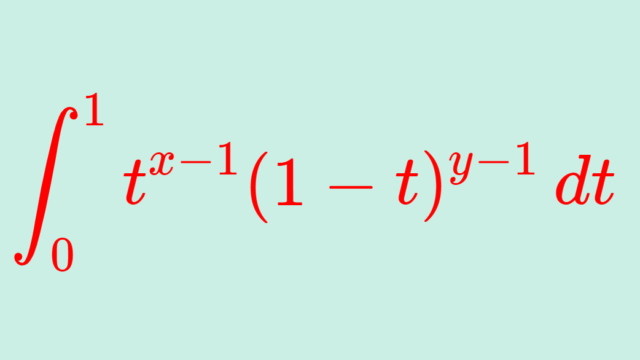 微分積分学(大学)
微分積分学(大学) 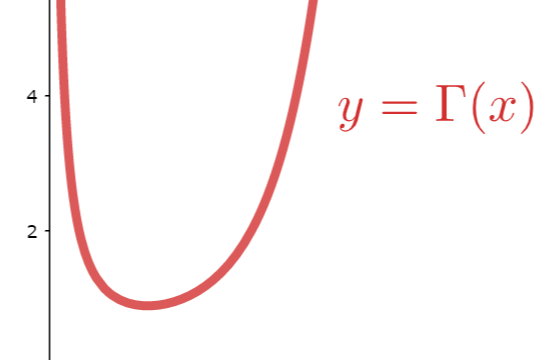 微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学) 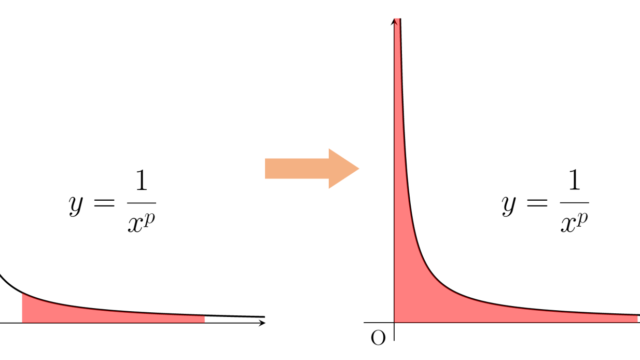 微分積分学(大学)
微分積分学(大学) 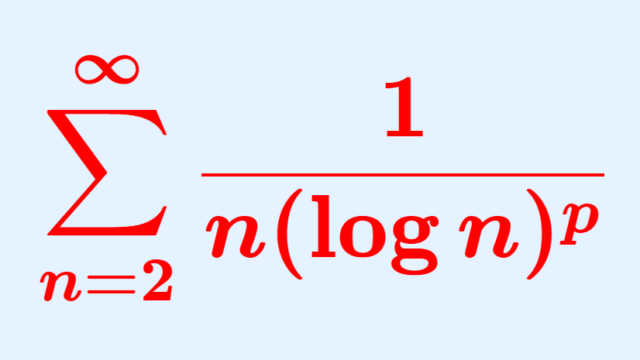 微分積分学(大学)
微分積分学(大学) 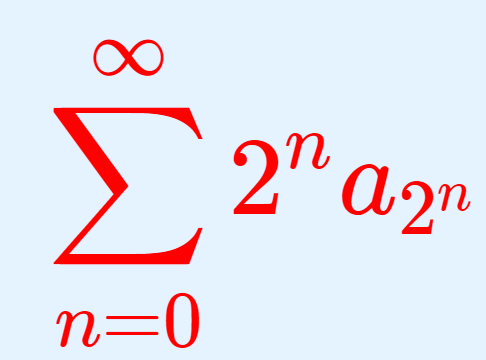 微分積分学(大学)
微分積分学(大学) 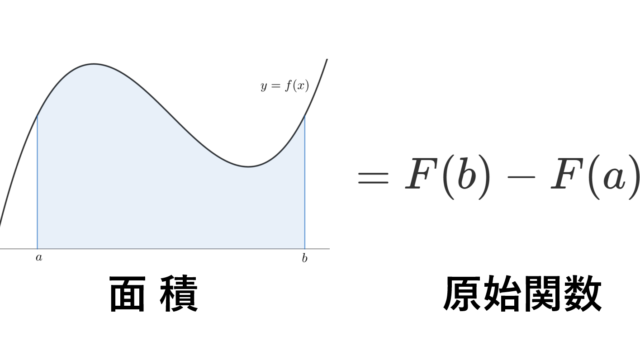 微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)