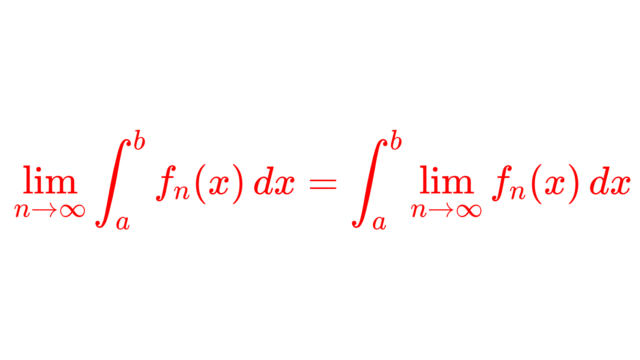 測度論
測度論 極限と積分の順序交換定理6つと交換できない例3つまとめ
極限と積分の順序交換定理6つの主張をまとめて紹介し,さらに極限と積分が交換できない例についても述べましょう。本記事はまとめ記事とし,実際の証明などは定理の主張後にあるリンク先を見てください。
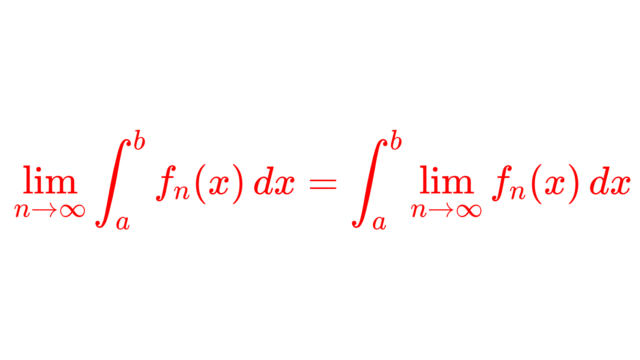 測度論
測度論 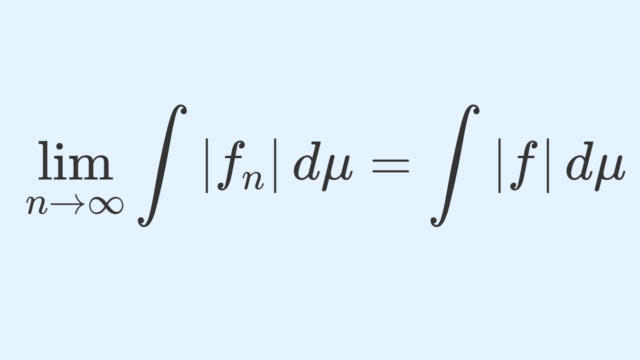 測度論
測度論 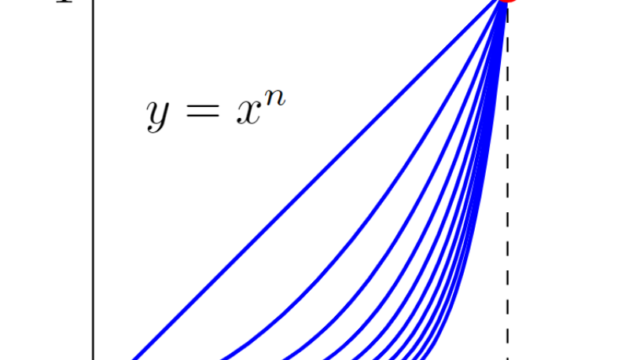 測度論
測度論 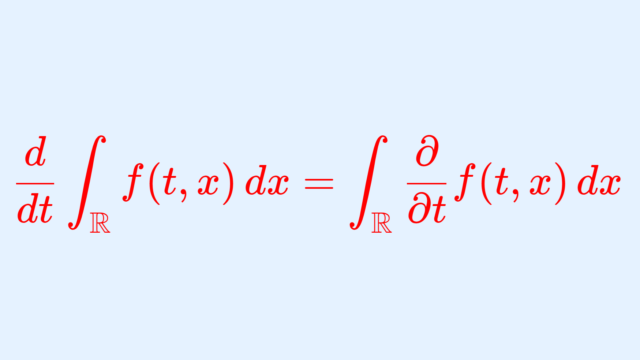 測度論
測度論 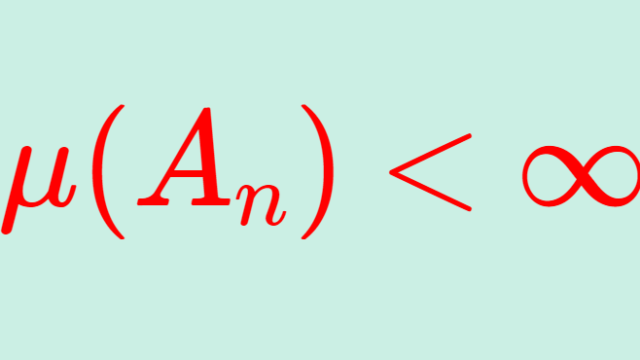 測度論
測度論 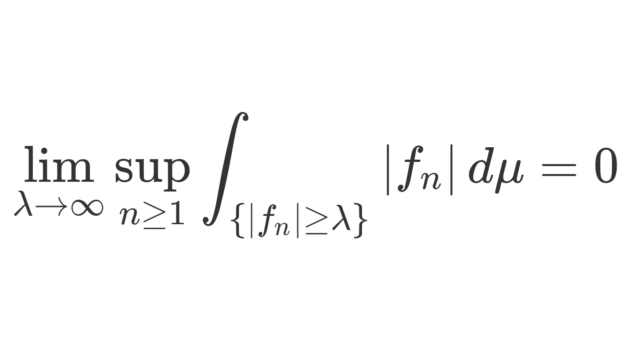 測度論
測度論 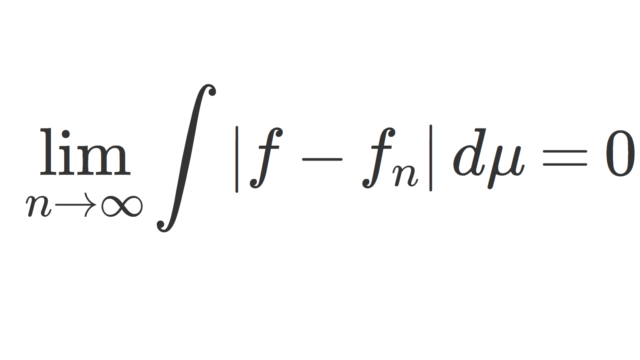 測度論
測度論 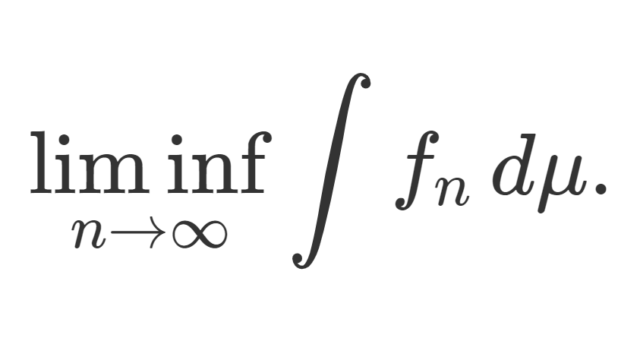 測度論
測度論 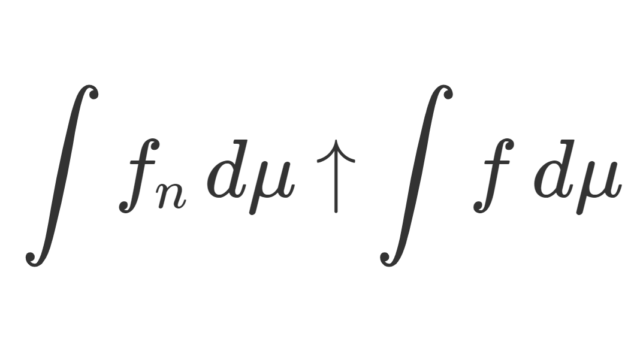 測度論
測度論 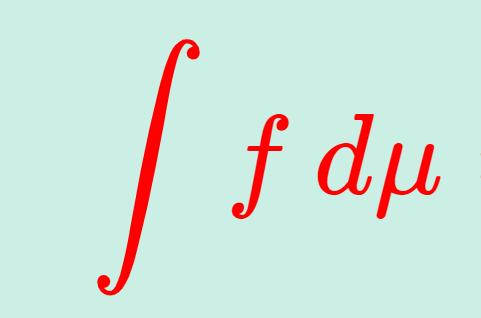 測度論
測度論