 微分積分学(大学)
微分積分学(大学) 包絡線とは~定義と求め方と例題4つ~
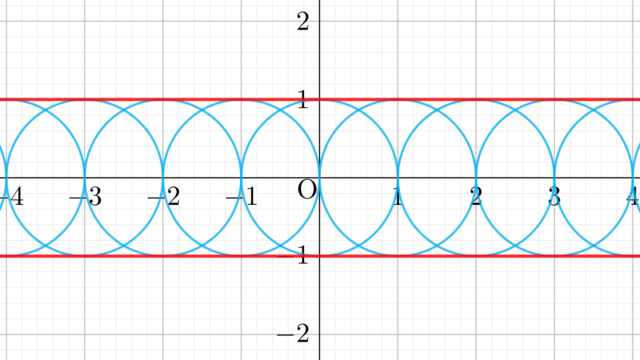
「包絡線 (envelope) 」とは,曲線族全てに接しているような曲線のことを言います。これについて,その厳密な定義と,求め方の例題を解説しましょう。
 微分積分学(大学)
微分積分学(大学)  複素関数論
複素関数論  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相 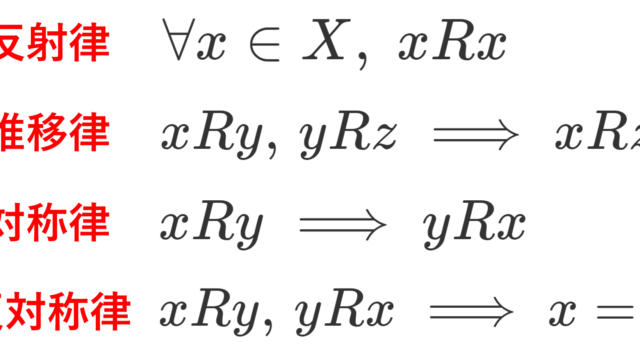 集合と位相
集合と位相 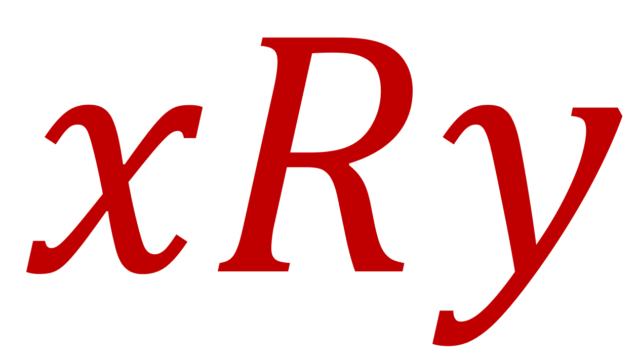 集合と位相
集合と位相 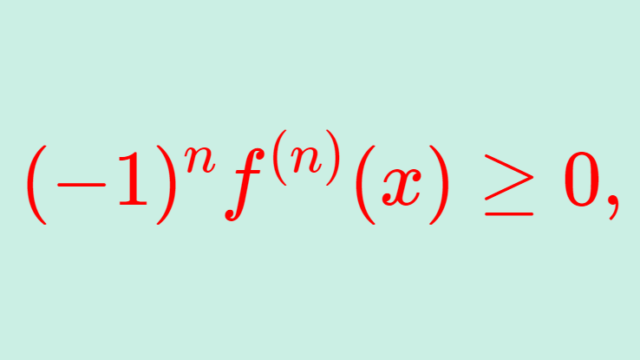 解析学(大学)その他
解析学(大学)その他 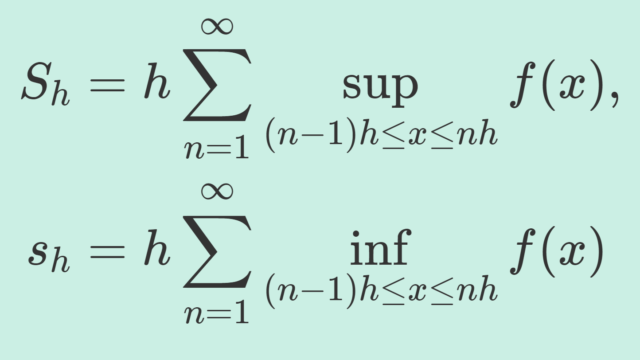 解析学(大学)その他
解析学(大学)その他  微分積分学(大学)
微分積分学(大学)