 微分積分学(大学)
微分積分学(大学)逆双曲線関数の導出とグラフと性質(微分・積分など)まとめ
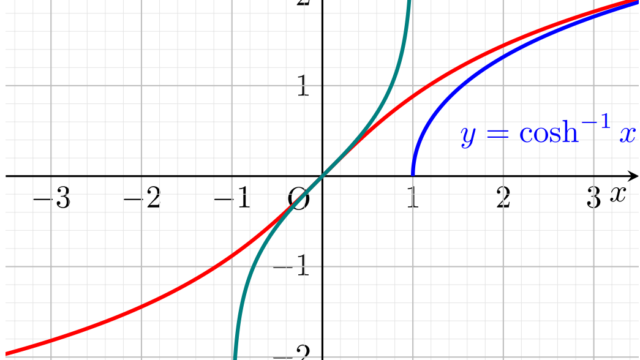
逆双曲線関数ともいう,双曲線関数 sinh, cosh, tanh の逆関数 sinh^{-1}, cosh^{-1}, tanh^{-1} (arcsinh, arccosh, arctanh) について,その定義と導出,グラフと性質(微分・積分など)をまとめましょう。
 微分積分学(大学)
微分積分学(大学)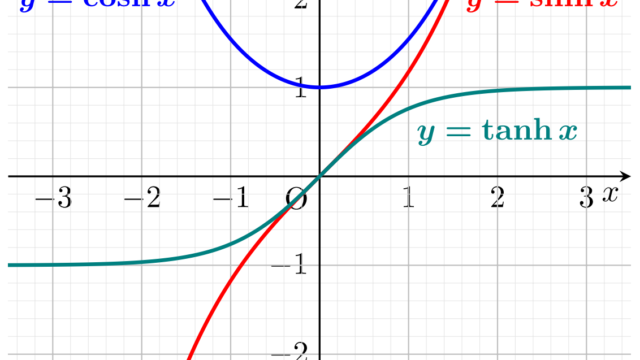 微分積分学(大学)
微分積分学(大学) 微分積分学(大学)
微分積分学(大学) 微分積分学(大学)
微分積分学(大学)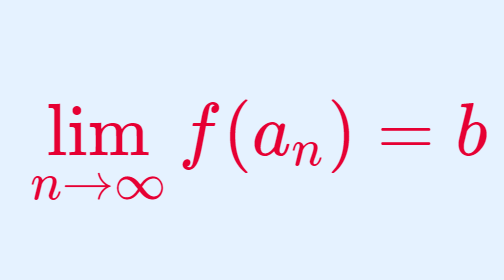 微分積分学(大学)
微分積分学(大学)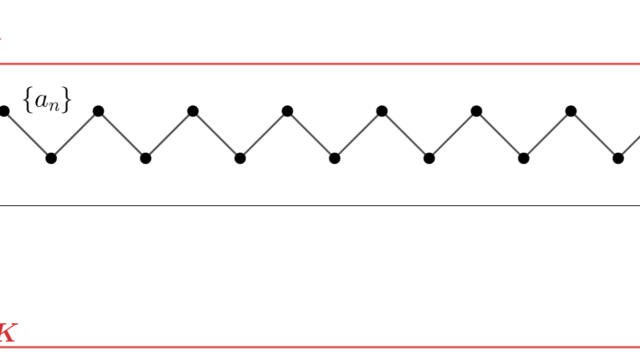 微分積分学(大学)
微分積分学(大学)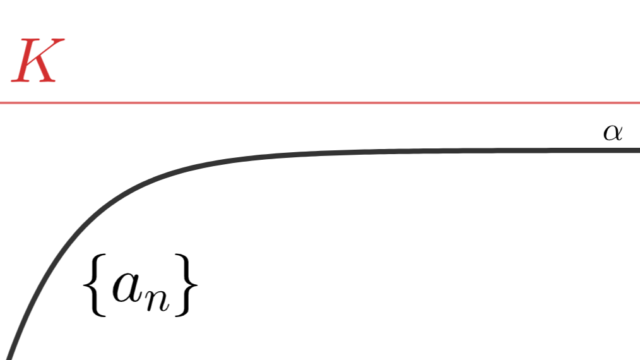 微分積分学(大学)
微分積分学(大学)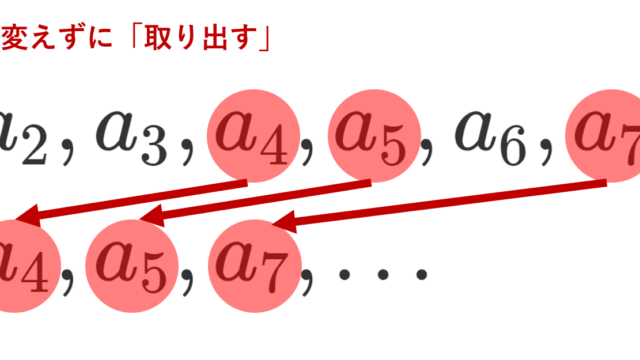 微分積分学(大学)
微分積分学(大学)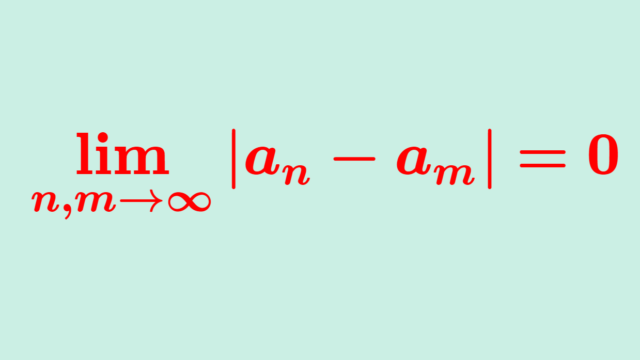 微分積分学(大学)
微分積分学(大学)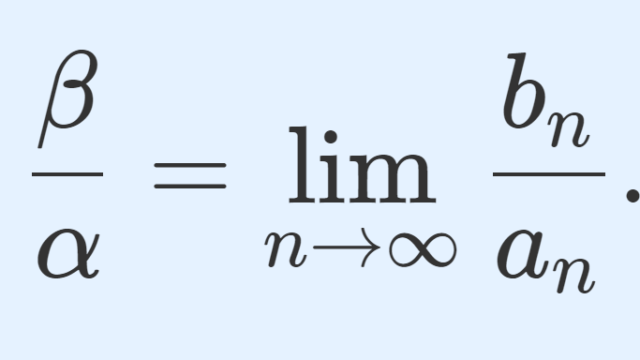 微分積分学(大学)
微分積分学(大学)