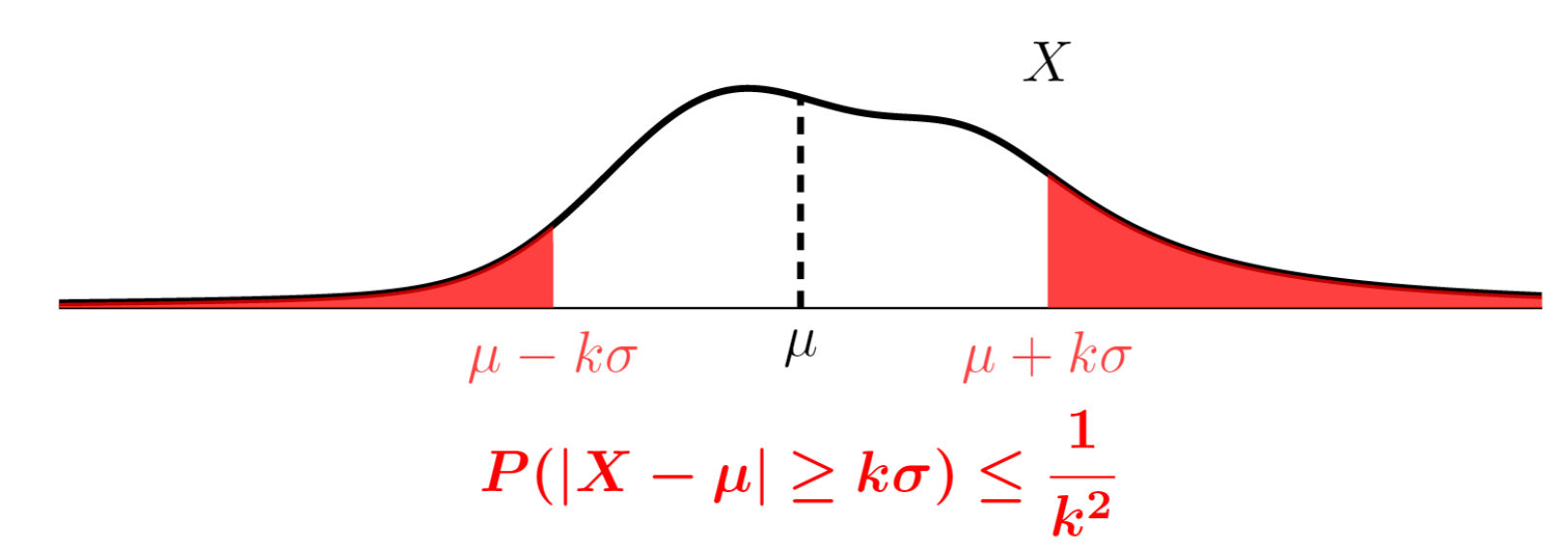
【確率論】チェビシェフの不等式とその例題・証明

チェビシェフの不等式とは，裾の確率を上から評価する不等式

\begin{gathered}P(|X|\ge a)\le \frac{E[|X|^2]}{a^2}, \\ P(|X-\mu|\ge k\sigma )\le \frac{1}{k^2} \end{gathered}

を指します。これについて，例題や証明を理解していきましょう。

チェビシェフの不等式

定理（チェビシェフの不等式; Chebyshev’s inequality）

$X$ を実数値確率変数とする。このとき， $a>0$ に対して，

\color{red}\large \begin{equation}P(|X|\ge a)\le \frac{E[|X|^2]}{a^2}\end{equation}

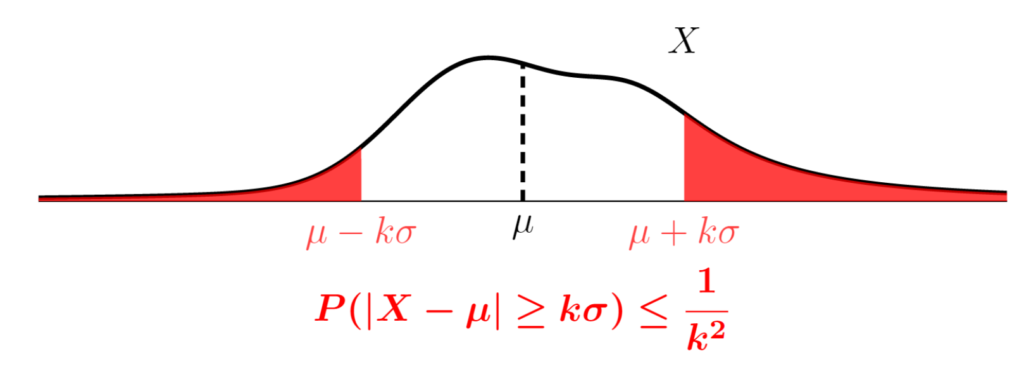
が成り立つ。またこれより， $X$ が有限の期待値 $\mu$ と分散 $\sigma^2$ をもつとき， $k>0$ に対して

\color{red}\large \begin{equation} P(|X-\mu|\ge k\sigma )\le \frac{1}{k^2}\end{equation}

が成立する。

$(2)$ 式は統計学でもよく使われます。 $X$ の分布が一切わかっていなくても，期待値と分散が分かっていれば，期待値からどのくらい遠くなりうるかが分かると言っているわけです。有用な定理ですね。

もちろん， $X$ は離散分布でも連続分布でも特異分布でも使える定理です。

一つだけ，実用的な例を紹介しましょう。

例題

あるテストの平均点は $\mu=55$ で，標準偏差 $\sigma=10$ であった。平均点から $20$ 点以上離れている人の割合としてあり得る最大値を，チェビシェフの不等式を用いて求めよ。

確率論というか統計学の問題ですが， $X$ を得点分布とし， $P(X=a)$ を「 $a$ 点を取った人数 / 全員の人数」と考えれば，離散確率変数 $X$ を扱う問題に帰着します。よって確率論の問題と思ってよいです。

実際に解いていきましょう。チェビシェフの不等式(2)において， $k=2$ とすれば，

P(|X-55|\ge 2\cdot 10 )\le \frac{1}{2^2} =25\%

なので，答えは $25\%$ ですね。 $\mu=55$ は実質的に用いませんでした。

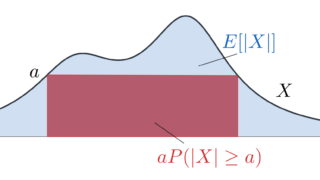
チェビシェフの不等式を証明するために，より原始的なマルコフの不等式というものを用います。主張を述べましょう。

マルコフの不等式

$X$ を実数値確率変数かつ $a>0$ とする。このとき，

\color{red} P(|X|\ge a) \le \dfrac{E[|X|]}{a}

が成立する。

証明は以下で行っています。

これを認めたうえで，チェビシェフの不等式

$\begin{align}P(|X|\ge a)\le \frac{E[|X|^2]}{a^2}, \tag{1}\end{align}$ $\begin{align} P(|X-\mu|\ge k\sigma )\le \frac{1}{k^2}\tag{2} \end{align}$

を証明しましょう。

証明

(1)式について

マルコフの不等式を確率変数 $X^2$ に適用して，

P(|X|\ge a) =P(|X|^2\ge a^2 )\le \dfrac{E[|X|^2]}{a^2} .

(2)式について

(1)式を確率変数 $X-\mu$ に適用して， $a=k\sigma$ とすると

P(|X-\mu |\ge k\sigma)\le \dfrac{E[|X-\mu|^2]}{k^2\sigma^2} .

ここで，分散の定義は $\sigma^2=E [|X-\mu|^2]$ であるから，

P(|X-\mu |\ge k\sigma)\le \dfrac{1}{k^2} .

証明終

マルコフの不等式さえ認めれば，証明は非常にシンプルだと思います。

なお，(1)の証明を $X^p \;(p>0)$ で行うことで，

P(|X|\ge a)\le \frac{E[|X|^p]}{a^p}

も証明できますね。