位相空間における連結性とは,その空間が互いに素な(互いに共通部分をもたない)2つの開集合で分割できないことをいいます。これは,開かつ閉である部分集合が空集合と全体集合に限ることと同値です。連結性は「ひとつながり」を想起させる概念です。
連結性について,その定義と基本的性質を紹介しましょう。
連結性の定義
定義(連結)
(X,\mathcal{O}) を空でない位相空間とする。 X が連結 (connected) あるいは連結空間 (connected space) であるとは,次の同値な2つの概念のうち,いずれか(したがって両方)が成立することをいう。
- A, B\in \mathcal{O}\setminus \{\emptyset\} で,
\Large\color{red} A\cap B=\emptyset, \quad A\cup B = X
となるものが存在しない。 - 開かつ閉である部分集合は \emptyset と X に限る。
部分集合 A\subset X が連結集合 (connected set) であるとは,相対位相に対して部分空間として連結であることをいう。連結でない集合を不連結 (disconnected) という。
開かつ閉である集合は英語で clopen set ということがあります。closed + open って感じですね。
1. \iff 2.は,1.で B = X\setminus A であることと,閉集合は開集合の補集合であることを考えるとほぼ明らかです。実際, A, B\in \mathcal{O}\setminus \{\emptyset\} で,
A\cap B=\emptyset,\, A\cup B = X となるものが存在する \iff A は A\ne \emptyset, X をみたす開かつ閉な部分集合です。

定義だけではイメージしにくいので,具体例を挙げましょう。
連結とそうでないものの具体例
例1(密着位相).
(X,\{\emptyset, X\}) を密着空間とすると, X は連結である。また任意の空でない部分集合 A\subset X は連結である。
開集合は空集合と全体集合しかないので明らかですね。
例2(離散位相).
(X,2^X) を離散空間とすると, A\subset X が連結である必要十分条件は, A が1点集合であることである。
A が2点以上の場合は, A を2つの空でない集合に分割できます。離散空間においては,任意の集合が開集合ですから,これは2つの空でない開集合で分割できたことになり,連結ではありません。
例3( \R).
a<b に対し,区間 (a,b), [a,b], [a,b), (a,b] や, (-\infty, b), (-\infty, b], (a, \infty), [a,\infty), \R などは全て連結である。
(0,1)\cup (2,3) や \{0, 1\} や有理数全体の集合 \mathbb{Q} は連結でない。
まず,後半について示しましょう。 (0,1)\cup (2,3) が連結でないことは,この集合が2つの互いに素な(すなわち共通部分をもたない)開集合 (0,1), (2,3) に分割できることから言えます。 \{0,1\} が連結でないことは,この集合が,この集合における2つの互いに素な開集合 \{0\},\{1\} に分割できることから言えます。
また,\mathbb{Q} が連結でないことは,たとえば \mathbb{Q} を2つの互いに素な開集合 (-\infty,\sqrt{2})\cap \mathbb{Q} と (\sqrt{2}, \infty)\cap\mathbb{Q} に分割できることから分かります。
さて逆に,前半について示しましょう。まず [a,b] が連結であることを示します。実数の連続性が大きく関係しています。
[a,b] が連結であることの証明
[a,b] が不連結と仮定すると,ある互いに素な開集合 A, B\subset [a,b] があって, A\cup B=[a,b] とできる。
同じことなので, b\in B としてよい。 B は開集合なので,ある \varepsilon_1>0 があって, (b-\varepsilon_1, b]\subset B である。特に, c=\sup A とすると, c<b である。
c\in A と仮定すると, A は開集合なのである \varepsilon_2>0 が存在して (c-\varepsilon_2, c+\varepsilon_2)\subset A であるが,これは \sup A \ge c+\varepsilon_2 となって矛盾する。 c\in B と仮定すると, B は開集合なのである \varepsilon_3>0 が存在して (c-\varepsilon_3, c+\varepsilon_3)\subset B となるが,これは \sup A\le c-\varepsilon_3 となって矛盾する。
以上から, [a,b] は連結である。
証明終
(a, b)=\bigcup_{n=1}^\infty [a+1/n,b-1/n], \: \R = \bigcup_{n=1}^\infty [-n, n] などと後の定理3より,残りの連結性も従います。
例4(補有限位相).
X を無限集合とし,
\mathcal{O}_f=\{\emptyset\}\cup \{ O\subset X\mid X\setminus O \text{ is finite}\}
を,補集合が有限集合である部分集合全体(と \{\emptyset\} との和集合)とすると, (X,\mathcal{O}_f) は位相空間になる。この位相を補有限位相 (cofinite topology, finite complement topology) という。この空間は連結である。
U, V\subset X をともに空でない開集合とすると, U\cap V\ne\emptyset となります。よって,そもそも U\cap V=\emptyset となるような空でない開集合 U,V を取ることができません。このような空間を hyperconnected といいます(→hyperconnected(既約位相空間)とultraconnected)。hyperconnected なら連結です。
補有限位相のその他の性質については,補有限位相と補可算位相について掘り下げるで解説しています。
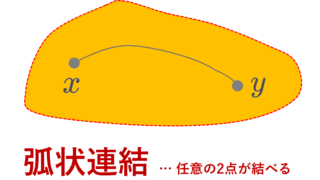
以上の例から,連結とは「ひとつながり」になっているというイメージを持ったかもしれません。このイメージは正しいとは言い切れません。「ひとつながり」はどちらかというと弧状連結という概念の方が近いです。弧状連結については,弧状連結・弧連結について定義・具体例・性質で解説しています。弧状連結ならば連結ですが,逆は必ずしも成立しません。これも弧状連結・弧連結について定義・具体例・性質で解説しています。
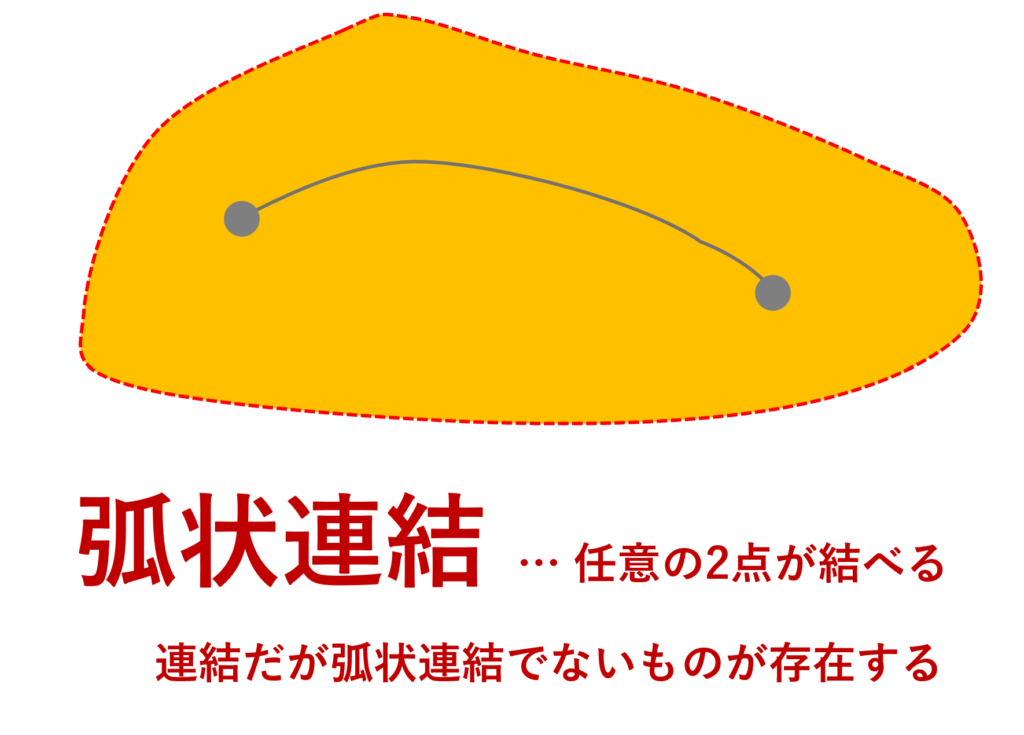
ただし,「連結」にひとつながりのイメージを持つことは間違えているかと言われると,それもまた微妙です。例えば後の定理5で紹介しますが,「ひとつながり」のイメージと密接に関係している中間値の定理は,弧状連結でなく連結のみで成立します。
連結空間の性質
連結性の主な性質を証明付きで紹介しましょう。
1. 連結空間の連続像は連結
定理1(連結空間の連続像は連結)
(X, \mathcal{O}_X), (Y,\mathcal{O}_Y) を位相空間とし,f\colon X\to Y を連続とする。
A\subset X を連結とするとき,その像 f(A)\subset Y も連結である。
証明
(A, \mathcal{O}_A) を (X, \mathcal{O}_X) から定まる相対位相とし, (f(A), \mathcal{O}_{f(A)}) を (Y,\mathcal{O}_Y) から定まる相対位相とする。このとき,定義域と終域を制限した写像 f\colon A\to f(A) は全射であり,さらに連続である(→位相空間における連続写像の定義と性質を詳しく)。記号を乱用して,これ以降この f について考える。
f(A) が不連結と仮定すると, V_1, V_2\in\mathcal{O}_{f(A)}\setminus \{\emptyset\} であって,
V_1\cap V_2=\emptyset, \quad V_1\cup V_2=f(A)
であるものが存在する。このとき, f^{-1}(V_1), f^{-1}(V_2)\in\mathcal{O}_A\setminus \{\emptyset\} であり,
となる。これは, A の連結性に矛盾している。以上から, f(A) は連結である。
証明終
2. 連結集合の閉包は連結
定理2(連結集合の閉包は連結)
(X,\mathcal{O}) を位相空間とし, A\subset X は連結とする。このとき
\large A\subset B\subset \overline{A}
をみたす任意の集合 B\subset X は連結である。特に, \overline{A} も連結である。
証明
X を B に置き換える(相対位相で部分空間と考える)と, A の閉包は B になるから, \overline{A} が連結であることを示せば十分である。
\overline{A} が不連結と仮定する。このとき,\overline{A} における空でない開集合 U, V\subset \overline{A} が存在して,
U\cap V = \emptyset,\quad U\cup V=\overline{A}
とできる。このとき, U\cap A, V\cap A は A における空でない(※後述)開集合で,
となる。これは, A の連結性に矛盾する。以上から, \overline{A} は連結である。
※の部分について
U\cap A\ne\emptyset を示そう。 U\cap A=\emptyset と仮定する。このとき, A\subset \overline{A}\setminus U となり,右辺は \overline{A} における閉集合であるから,
\overline{A}\subset \overline{A}\setminus U
となる。よって, U=\emptyset となって矛盾する。ゆえに, U\cap A\ne \emptyset が示せた。全く同様に V\cap A\ne\emptyset である。
証明終
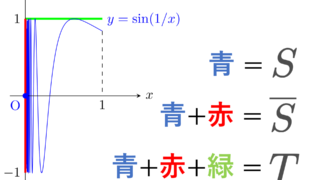
定理2は重要かつ強力な性質です。たとえば, S=\left\{\bigl(x, \sin(1/x)\bigr)\in\R^2\middle| 0<x\le 1\right\} は連結なので,その \R^2 における閉包 \overline{S}= S\cup (\{0\}\times [-1, 1]) も連結だと分かります。ただし, \overline{S} はいわゆる「ひとつながり」(弧状連結)ではありません。この辺については,以下で解説しています。
3. 連結集合のつながった和集合は連結
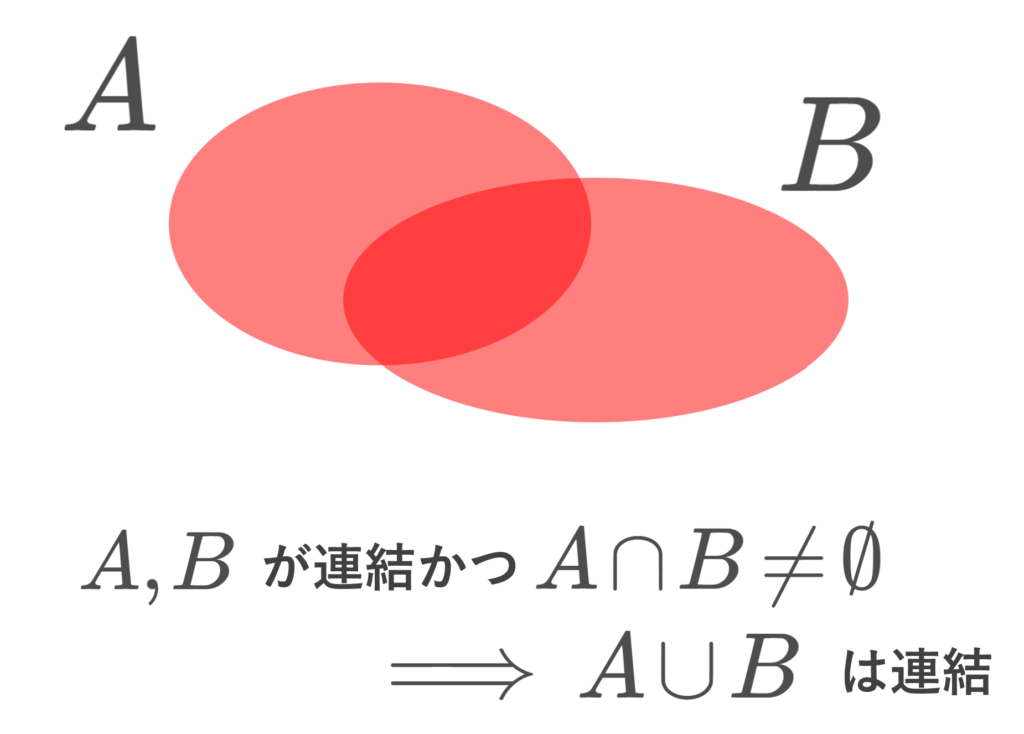
定理3(連結集合のつながった和集合は連結)
(X,\mathcal{O}) を位相空間とする。
- \{A_\lambda\}_{\lambda\in \Lambda} を連結な集合族とし,任意の \lambda_1, \lambda_2\in\Lambda に対し, A_{\lambda_1}\cap A_{\lambda_2}\ne \emptyset とすると, A=\bigcup_{\lambda\in \Lambda} A_\lambda も連結である。特に,\bigcap_{\lambda\in\Lambda} A_\lambda\ne\emptyset のとき, A=\bigcup_{\lambda\in \Lambda} A_\lambda は連結である。
- \{A_n\}_{n=1}^\infty を連結な集合族とし,任意の n\ge 1 に対し, A_n\cap A_{n+1}\ne \emptyset とする。このとき,A=\bigcup_{n=1}^\infty A_n も連結である。
- 任意の x,y\in X に対し,ある x,y\in A_{x,y} となる連結な A_{x,y}\subset X が存在するならば, X は連結である。
証明
1.について
U, V\subset A を A における開集合で, U\cap V=\emptyset かつ U\cup V = A とする。このとき, U\cap A_\lambda, V\cap A_\lambda は A_\lambda における開集合であり, A_\lambda の連結性から,
U\cap A_\lambda = A_\lambda ,\quad V\cap A_\lambda=\emptyset
または
のいずれかが成立する。もし, \lambda_1\ne \lambda_2 に対し,
が同時に成立するとすると,
となって仮定に矛盾する。ゆえに,任意の \lambda\in \Lambda に対し,
としてよい。これにより, U=A, V=\emptyset となるから, A は連結である。
2.について
1.を帰納的に用いることで, B_n=A_1\cup \cdots \cup A_n は連結である。 A_1=\bigcap_{n=1}^\infty B_n であるから,1.が適用できて, A=\bigcup_{n=1}^\infty B_n は連結である。
3.について
a\in X を固定し, X=\bigcup_{x\in X} A_{a,x} であることと,1.から従う。
証明終
4. 連結空間の直積は連結
定理4(連結空間の直積は連結)
\{(X_\lambda,\mathcal{O}_\lambda)\}_{\lambda\in\Lambda} を連結な位相空間の族とする。このとき,その直積 X=\prod_{\lambda\in\Lambda} X_\lambda も連結である。
なお, X が連結なら逆に各 X_\lambda も連結と言えます。これは,射影 X\to X_\lambda が連続な全射であることと,定理1からわかります。
証明
まず, \Lambda が有限集合のときに示そう。 X_1, X_2 が連結のとき, X_1\times X_2 が連結であることを示せば,後は帰納的にわかるから十分である。
(x_1, x_2), (y_1, y_2)\in X_1\times X_2 に対し, M_1=X_1\times \{y_2\}, \, M_2=\{x_1\}\times X_2 とすると, M_1\cong X_1, \, M_2\cong X_2 ( \cong は同相の意味)であるので, M_1,M_2 は連結である。 (x_1, y_2)\in M_1\cap M_2 と定理3.1より, M=M_1\cup M_2 は連結である。 (x_1, x_2), (y_1, y_2)\in M なので,定理3.3から, X_1\times X_2 は連結である。
次に,一般の \Lambda について示そう。 a=(a_\lambda)\in X を一つ固定する。
n\ge 1,\, \lambda_1, \ldots, \lambda_n \in \Lambda とし,
\begin{aligned}&M_{\lambda_1, \ldots, \lambda_n} \\&= \{ (x_\lambda)\in X\mid a_\lambda= x_\lambda\text{ for } \lambda\ne \lambda_1,\ldots, \lambda_n\}\end{aligned}
とすると, M_{\lambda_1, \ldots, \lambda_n} \cong X_{\lambda_1}\times \cdots\times X_{\lambda_n} であるから,前半の議論により M_{\lambda_1, \ldots, \lambda_n} は連結である。 a\in M_{\lambda_1, \ldots, \lambda_n} であるから,定理3.1より,
と定めると, M は連結である。 \overline{M}=X を示せば,定理2より X は連結と分かるので, \overline{M}=X を示そう。
直積位相の定義より, X の任意の空でない開集合 O は,ある n\ge 1,\, \lambda_1, \ldots, \lambda_n があって,さらに空でない開集合 U_{\lambda_1}\in\mathcal{O}_{\lambda_1}, \ldots, U_{\lambda_n}\in\mathcal{O}_{\lambda_n} があって,
U_{\lambda_1}\times\cdots\times U_{\lambda_n}\times\prod_{\lambda\ne \lambda_1,\ldots, \lambda_n} X_\lambda
の形の開集合を含む。 M_{\lambda_1, \ldots, \lambda_n} はこの集合と共通部分をもつから, O\cap M\ne \emptyset となる。ゆえに, \overline{M}=X が示された。
証明終
定理4と \R の連結性より, \R^n は連結です。
5. 中間値の定理
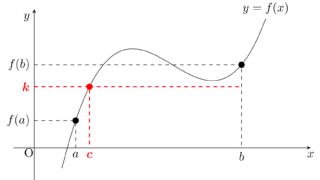
中間値の定理は, f\colon \R\to \R バージョンを理系の高校生でも学習しますが,より一般に,連結な位相空間上の実数値連続写像でも成立します。中間値の定理は,連結性が大きく関わっているわけですね。
定理5(中間値の定理)
(X,\mathcal{O}) を連結な位相空間とし, f\colon X\to \R を連続とする。さらに, x_1, x_2\in X に対し, f(x_1)<f(x_2) とする。このとき,任意の f(x_1)<\gamma <f(x_2) に対し,ある x\in X が存在して, f(x)=\gamma とできる。
要するに, \alpha, \beta \in f(X),\, \alpha<\beta ならば,[\alpha,\beta]\subset f(X) ということです。
証明
X は連結かつ f は連続なので,定理1から, f(X) は連結である。 \alpha, \beta \in f(X),\, \alpha<\beta ならば,[\alpha,\beta]\subset f(X) を示せば十分である。
もし, \alpha<\gamma<\beta で, \gamma \notin f(X) となるものが存在すると仮定すると, f(X) は2つの開集合 (-\infty, \gamma)\cap f(X) と (\gamma, \infty)\cap f(X) に分割することができるから, f(X) の連結性に矛盾する。
よって,全ての \alpha<\gamma<\beta で, \gamma\in f(X) なので, [\alpha, \beta]\subset f(X) である。
証明終
より基本的な f\colon \R\to \R バージョンの中間値の定理は以下で証明しています。
連結性に関連する概念
連結性に関する概念を列挙しておきましょう。
| 名称 | 定義 |
|---|---|
| 連結 (connected) | 2つの互いに素な空でない開集合 U,V で, U\cup V=X となっているものは存在しない |
| 弧状連結 (path connected) | 任意の異なる2点 x,y\in X について,ある連続写像 f\colon [0,1]\to X で, f(0)=x, f(1)=y となるものが存在する |
| 弧連結 (arc connected) | 上の f として,埋め込みすなわち f\colon [0,1]\to f([0,1]) が同相となっているものが常に取れる(※[3]では単に全単射なものが取れるとしている。 X がハウスドルフ ( T_2)なら弧状連結と弧連結は同値) |
| hyperconnected | 任意の空でない2つの開集合が常に共通部分を持つ |
| ultraconnected | 任意の空でない2つの閉集合が常に共通部分を持つ |
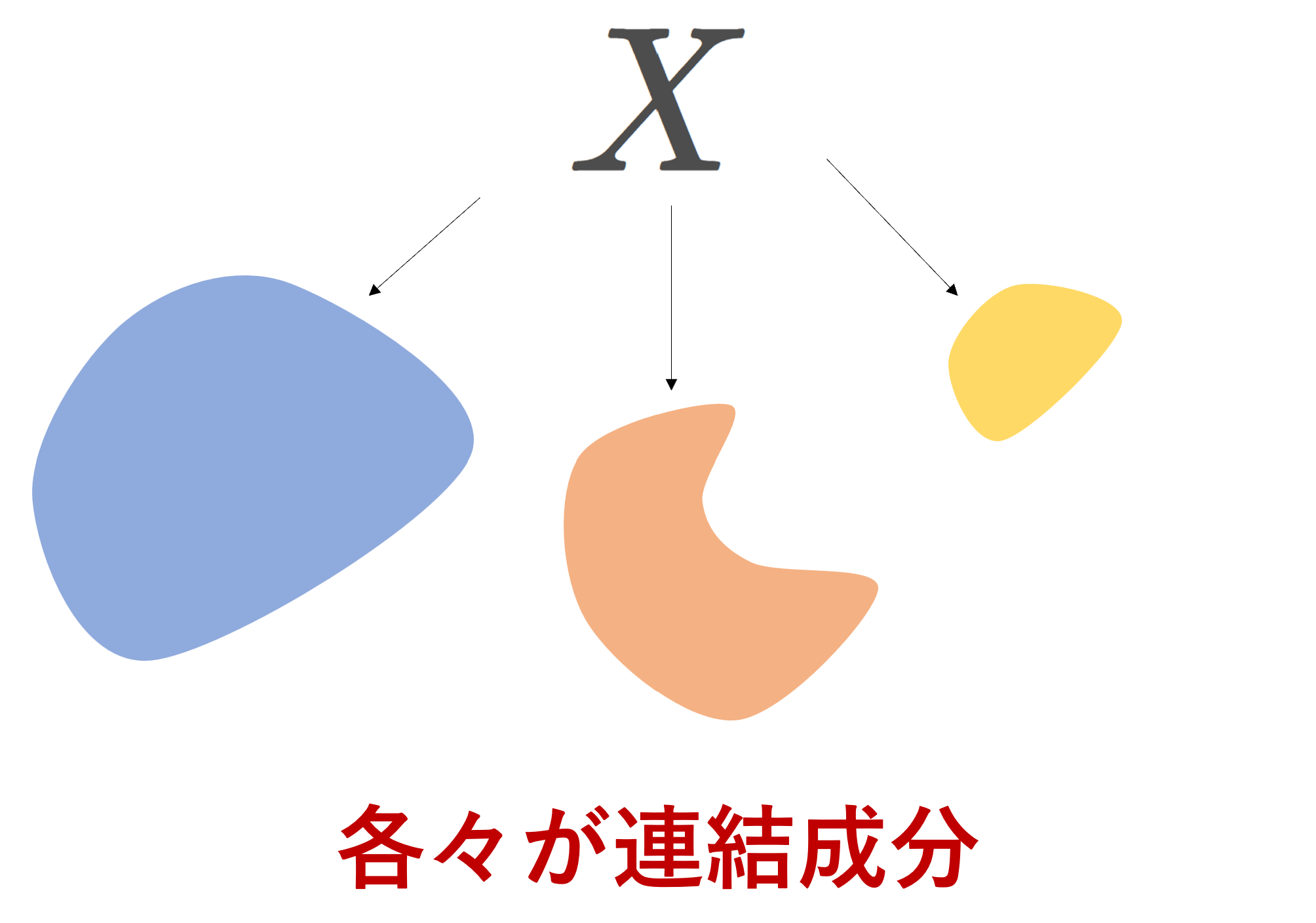
| 完全不連結 (totally disconnected) | 連結部分集合が1点集合のみ |
| 完全弧状不連結 (totally path disconnected) | 弧状連結部分集合が1点集合のみ |
| 局所連結 (locally connected) | 全ての点において,連結集合からなる基本近傍系を持つ |
| 局所弧状連結 (locally path connected) | 全ての点において,弧状連結集合からなる基本近傍系を持つ |
| 単連結 (simply connected) | f(0)=f(1) をみたす任意の連続写像 f\colon [0,1]\to X が定値写像とホモトピック |
参考
- 内田伏一「集合と位相」(裳華房 数学シリーズ, 増補新装版, 2020)
- 松坂和夫「集合・位相入門」 (岩波書店 数学入門シリーズ,新装版,2018)
- L. A. Steen, J. A. Seebach, Counterexamples in Topology, 2nd edition. Springer, 1978.
- S. Willard, General Topology, Dover Publications, 2004.