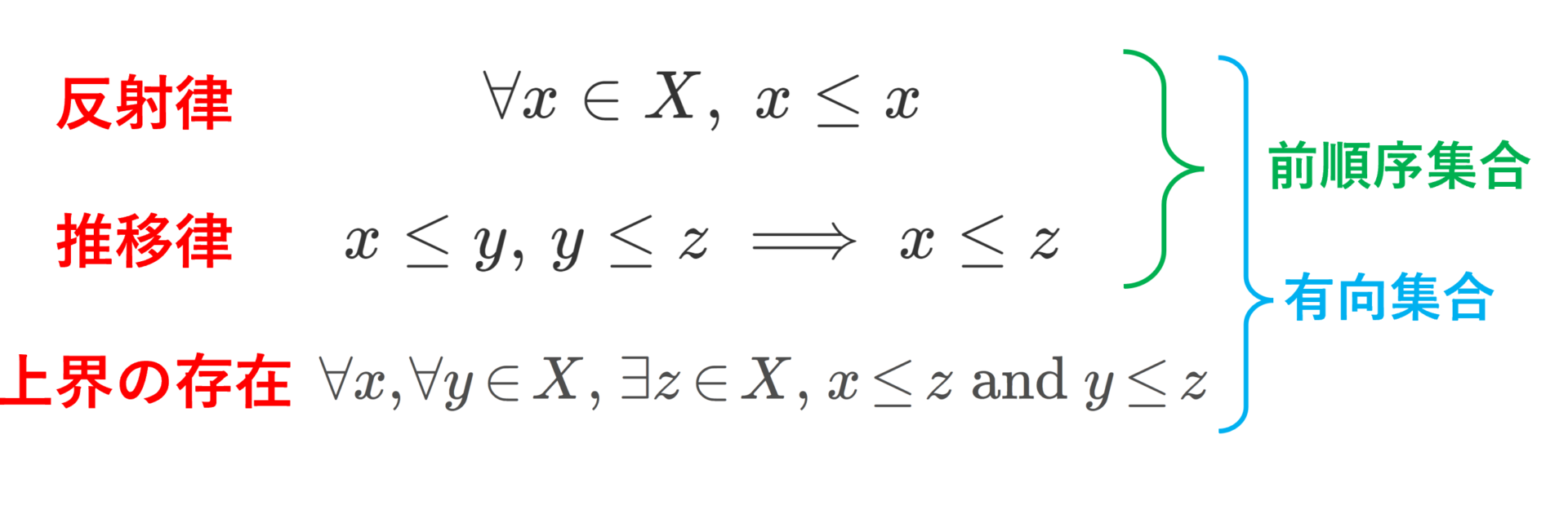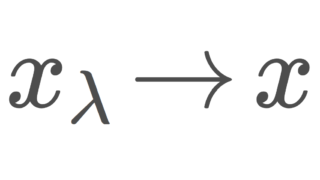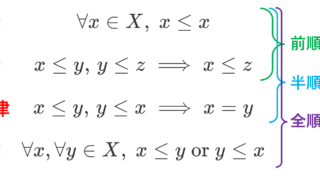有向集合とは，任意の2元に上界があるような前順序集合のことをいいます。位相空間におけるネット(有向点族)を定義する際の添え字としても用いられます。有向集合について，詳しく見ていきましょう。
有向集合の定義
定義（有向集合）
空でない集合 X 上の二項関係 \le について，
- 任意の x\in X について， x\le x (反射律)
- x,y,z\in X に対して， x\le y,\; y\le z ならば x\le z (推移律)
- 任意の x,y\in X に対して，ある z\in X が存在して， x\le z かつ y\le z が成立する (任意の2元の上界の存在)
が成り立つとき， (X, \le ) を有向集合 (directed set) という。
1,2.をみたす集合は前順序集合 (preorderd set) です。任意の2元に上界が存在する前順序集合が有向集合です。
ちなみに，1,2.に加えて， x\le y,\, y\le x\implies x=y (反対称律) を課した集合は半順序集合 (partially ordered set; poset) といいます。 上界が存在する半順序集合を有向集合と定義することもあります。
具体例をみましょう。
有向集合の具体例
例1(全順序集合).
\mathbb{Z},\mathbb{Q},\R は全て有向集合である。より一般に，任意の全順序集合は有向集合である。
全順序集合とは，半順序集合かつ任意の x,y に対して， x\le y か y\le x のいずれかが成立するような集合です。
例2(集合の包含).
X を集合とし， 2^X をべき集合とする。
このとき， A,B\in 2^X における包含順序を
A\le B\iff A\subset B
と定め，逆包含順序を
と定めると， (2^X, \le), (2^X, \le') はどちらも半順序かつ有向集合である。
また，集合 X 上の位相(開集合族) \mathcal{O} やσ加法族 \mathcal{F} も同じく，包含順序・逆包含順序のどちらで考えても半順序かつ有向集合である。
同じような例ですが，以下は位相空間論で大切です。
例3(近傍系).
(X,\mathcal{O}) を位相空間とする。
x\in X における近傍系(近傍全体の集合)を \mathcal{N}_x とすると， \mathcal{N}_x は逆包含順序 U\le V\iff U\supset V によって半順序かつ有向集合である。
U,V が x の近傍であるとき， U\cap V は x の近傍なので，これが上界の一つになりますね。
また， U\cup V も x の近傍なので，\mathcal{N}_x は通常の包含順序によっても半順序かつ有向集合です。しかし，位相空間論においては逆包含順序のほうがよく使います。なぜなら，「 x に収束する」みたいなことを考えたいからです。 たとえば， \R における通常の位相における x\in \R の近傍系 \mathcal{N}_x には，逆包含順序における最大元がありません。すると， x に収束する極限みたいなものを考えることができるのです。
この辺の概念はネット(有向点族)の話になるので，別の機会に解説しましょう。
例4(距離空間).
(X, d) を距離空間とし， a\in X とする。このとき， a からの近さによって，
x\le y \iff d(a, x)\ge d(a, y)
とすると， X\setminus \{a\} は一般に全順序集合・半順序集合ではないが，有向集合である。
x\le y, \,y\le x\implies x=y (反対称律)が一般に成立しないので，半順序集合や全順序集合ではありません。たとえば， d(a,x)=d(a,y) なら，x,y\in X の上界は x もそうだし， y もそうです。しかもこれらは最小上界です。このように，最小上界が複数あることもあり得ます。
不正確な表現ですが，この有向集合は， x\to\infty とすればするほど， a に近づくようなイメージです。
例5.
関数 f\colon \R\to \R の集合 F(\R,\R) において，
f\le g\iff \forall x\in \R,\, f(x)\le g(x)
と定めると， F(\R, \R) は半順序かつ有向集合である。
逆に有向集合でない簡単な例も挙げておきましょう。
例6.
集合 A=\bigl\{ \{a\}, \{b\}\bigr\} に，包含順序を入れた (A,\le) は半順序集合だが有向集合でない。
\{a\} と \{b\} に共通する上界がないので，有向集合ではないです。
有向集合の利用
位相空間論において，有向集合はネット(有向点族)の添え字として使われます。
普通の点列 (x_n) の添え字 n は正の整数の集合 \mathbb{N}=\{1,2,3,\ldots\} ですが，ネット(有向点族)の (x_\lambda) 添え字 \lambda は有向集合 \Lambda と考えます。この意味で，ネット(有向点族)は点列の一般化になっています。
n\to\infty とするのと同じように \lambda\to\infty みたいなことを考えて，ネット(有向点族)の収束を考えることで，一般の位相空間においても，直感に反しない収束の概念を獲得することができます。詳しくは，いずれまた別の記事で解説しましょう。
