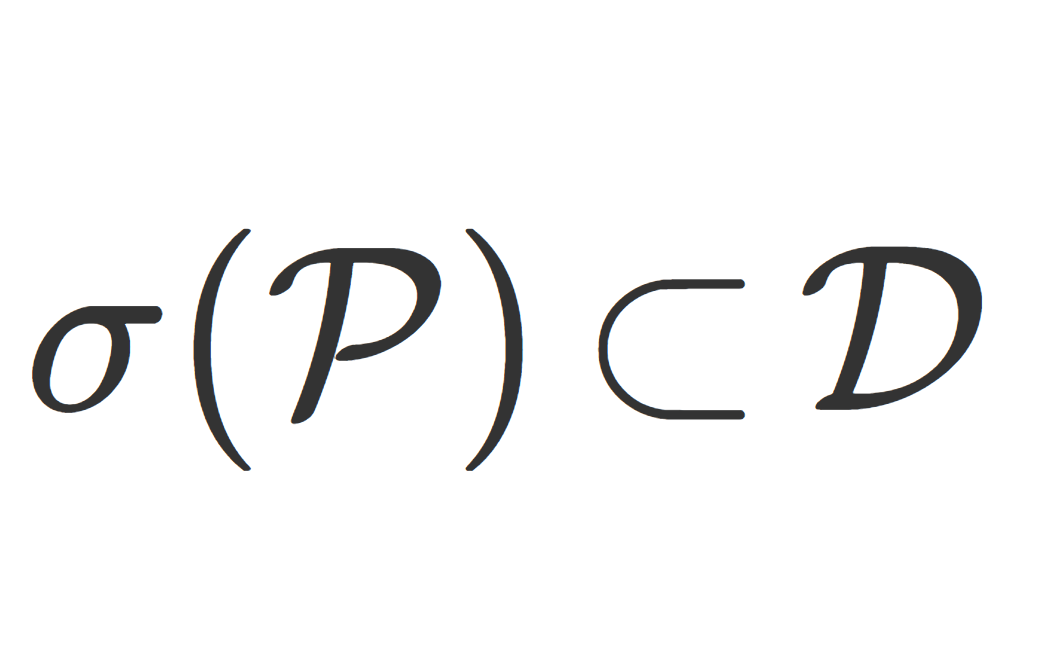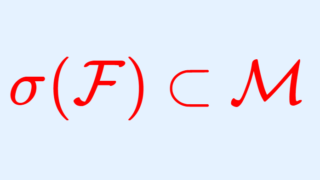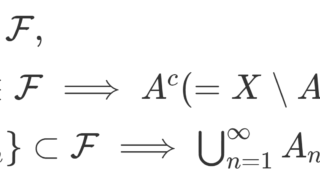ディンキン族定理あるいは,ディンキンの \pi\text{-}\lambda 定理とは,測度論の深い・複雑な議論を展開するにあたって重要な定理です。
本記事では,まずディンキン族定理に必要な \pi システム(乗法族)と \lambda システム(ディンキン族)の概念について定義し,ディンキン族定理を証明します。
πシステム(乗法族)とλシステム(ディンキン族)
まずはディンキン族定理を述べるためにいくつか用語を定義しておきます。
πシステム(乗法族)の定義と具体例
2^X とは,X のべき集合を指すことにします。
定義( \pi システム; \pi-system,乗法族)
集合 X に対し,X の部分集合族 \emptyset \ne \mathcal{P}\subset 2^X が \pi システム (\pi-system) または乗法族であるとは,
\large \color{red} A,B\in\mathcal{P}\implies A\cap B\in\mathcal{P}
が成り立つことをいう。
\mathcal{P} は共通部分に関して閉じている部分集合族というわけですね。
「 \mathcal{F} がσ-加法族 \implies \mathcal{F} が \pi システム」なのは明らかでしょう。また, \{\mathcal{P}_\lambda\} を \pi システムの族とするとき, \bigcap_{\lambda} \mathcal{P}_\lambda も \pi システムです。
\pi システム(乗法族)の具体例
X = \{1,2,3,4\} に対し,
\color{red}\mathcal{P} = \bigl\{\{2,3\}, \{1,2,3\}, \{2,3,4\} \bigr\}
とすると,\mathcal{P} は \pi システムである。
上の例は,σ-加法族でないが,\pi システムとなっている例ですね。
λシステム(ディンキン族)の定義と具体例
定義( \lambda システム; \lambda-system,ディンキン族)
集合 X に対し,X の部分集合族 \emptyset \ne \mathcal{D}\subset 2^X が \lambda システム (\lambda-system) またはディンキン族 (Dynkin system) であるとは,
- \color{red}X\in\mathcal{D}
- \color{red} A,B\in\mathcal{D},\, A\subset B\implies B\setminus A\in\mathcal{D}
- \color{red}\{A_n\}\subset \mathcal{D},\, A_n\uparrow A\implies A\in\mathcal{D}
の全てが成り立つことを言う。ただし, A_n \uparrow A とは, A_1\subset A_2\subset A_3\subset \cdots かつ A=\bigcup_{n=1}^\infty A_n となることをあらわす。
1,2.より,\emptyset = X\setminus X\in\mathcal{D} であり,また A\in\mathcal{D}\implies A^c = X \setminus A \in\mathcal{D} も成り立ちます。
「 \mathcal{F} がσ-加法族 \implies \mathcal{F} が \lambda システム」なのは明らかでしょう。 また, \{\mathcal{D}_\lambda\} を \lambda システムの族とするとき, \bigcap_{\lambda} \mathcal{D}_\lambda も \lambda システムです。 これは簡単な演習問題でしょう。
特に \mathcal{C}\subset 2^X に対し, \mathcal{C} を含む \lambda システムの集まり
\mathscr{D}=\{ \mathcal{C}\subset \mathcal{D}\colon \mathcal{D} \text{ is }\lambda\text{-system}\} \supset 2^X
を考えることができて, \mathcal{D}_0=\bigcap_{\mathcal{D}\in\mathscr{D}} \mathcal{D} とするとこれは \mathcal{C} を含む最小の \lambda システムになります。この議論から,ある集合族を含む最小の \lambda システムを常に考えることが可能です。この話はあとで使います。
\lambda システム(ディンキン族)の具体例
X=\{1,2,3,4\} に対し,
\mathcal{D}=\bigl\{\emptyset,\{1,2\}, \{1,3\}, \{2,4\},\{3,4\} ,X\bigr\}
とすると, \mathcal{D} は \lambda システム(ディンキン族)である。
上の \mathcal{D} は \lambda システムだがσ-加法族でない例になっています。
ディンキン族定理(π-λ定理)
さて,準備ができましたから,ディンキン族定理を述べましょう。
ディンキン族定理(π-λ定理)の主張
ディンキン族定理( \pi\text{-}\lambda 定理)
X の部分集合族 \mathcal{P}\subset \mathcal{D} について, \mathcal{P} が \pi システムであり, \mathcal{D} が \lambda システムであれば
\large\color{red}\sigma(\mathcal{P})\subset \mathcal{D}
が成立する。ただし, \sigma(\mathcal{P}) は \mathcal{P} から生成されるσ-加法族を指す。特に, \pi システムを含む最小の \lambda システムはσ-加法族である。
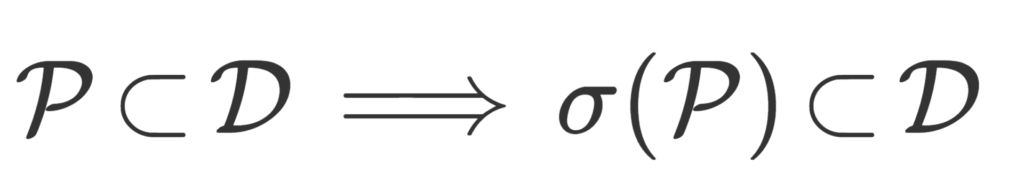
最後の「特に~」が大切です。σ-加法族であることを示すのが難しい場合に,代わりに \lambda システム(ディンキン族)であることを示して,σ-加法族であると帰結する際に使うことが多い定理です。確率論でもよく使われます。
ディンキン族定理(π-λ定理)の証明
証明の前に,σ-加法族の定義を確認しておきましょう。σ-加法族の定義を忘れていると,証明できませんからね。
X 上の集合族 \mathcal{F}\subset 2^X がσ-加法族であるとは,
- \emptyset \in\mathcal{F}
- A\in\mathcal{F}\implies A^c(=X\setminus A)\in\mathcal{F}
- \{A_n\}\subset \mathcal{F}\implies \bigcup_{n=1}^\infty A_n\in\mathcal{F}
の全てが成り立つことを言う。
詳しくはσ加法族と可測空間の定義・基本的な性質をわかりやすくを確認してください。
これを踏まえて,証明していきます。ちょっと長いですが頑張りましょう。あらすじは赤字で示してあります。
証明
\mathcal{D} を \mathcal{P} を含む最小の \lambda システム(ディンキン族)としたときに, \mathcal{D} がσ-加法族であることを示せばよい。(最小の \lambda システムを考えられることは前述した)
\mathcal{D} がσ-加法族の定義1,2.をみたすことはよい(既に述べた)。よって,σ-加法族の定義3.をみたすことを示せばよい。
一般に A\in \mathcal{D} に対し,
\mathcal{D}_A = \{ D\in\mathcal{D} \mid D\cap A\in\mathcal{D}\}
とすると, \mathcal{D} が \lambda システムであることから, 簡単な確認により \mathcal{D}_A\subset\mathcal{D} も \lambda システムであることに注意する。
まず P\in\mathcal{P}\subset\mathcal{D} とすると, \mathcal{D}_P は \lambda システムである。\mathcal{P} が \pi システムなので \mathcal{P}\subset \mathcal{D}_P\subset \mathcal{D} である。\mathcal{D} の最小性より,\mathcal{D}_P=\mathcal{D} となり,特に P\in\mathcal{P}, \,D\in\mathcal{D}\implies P\cap D\in\mathcal{D} が言える。
つづいて, A\in\mathcal{D} とすると, \mathcal{D}_A は \lambda システムであり,かつ上の議論より \mathcal{P}\subset\mathcal{D}_A もわかる。 \mathcal{D}_A\subset \mathcal{D} と \mathcal{D} の最小性より, \mathcal{D}_A=\mathcal{D} である。特に, A,B\in\mathcal{D}\implies A\cap B\in\mathcal{D} (\mathcal{D} は \pi システム)ということになる。
あと示すべきは「\mathcal{D} が \pi システムかつ \lambda システム \implies σ-加法族」だけである。 \mathcal{D} はσ-加法族の定義2.をみたすので, A,B\in\mathcal{D} とすると, A\cup B = (A^c\cap B^c)^c\in\mathcal{D} となる。よって \{A_n\}\subset\mathcal{D} に対し, B_n=\bigcup_{m=1}^n A_m とすると, B_n\in\mathcal{D} が言える。\lambda システムの定義3.より, B_n \uparrow \bigcup_{n=1}^\infty A_n \in\mathcal{D} となり, \mathcal{D} はσ-加法族の定義3.もみたす。
証明終