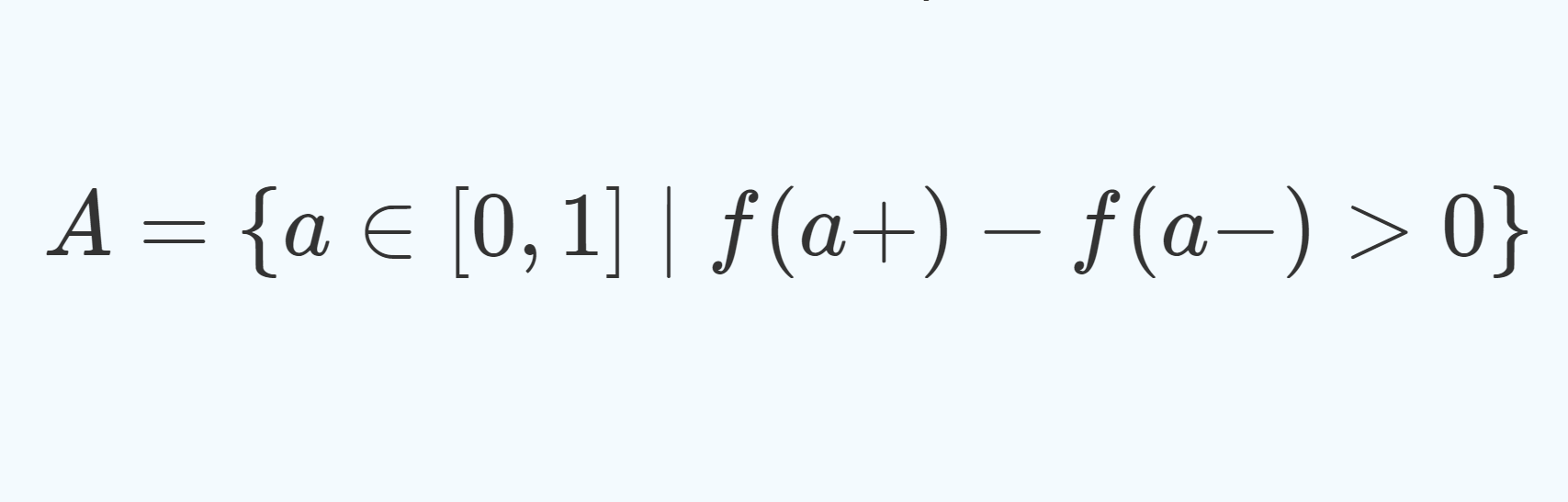【Frodaの定理】単調関数の不連続点は高々可算個であることの証明

証明

f は広義単調増加としてよい。また，区間 [n,n+1) における不連続点の集合を A^{(n)} とすると，不連続点全体の集合は \bigcup_{n=-\infty}^\infty A^{(n)} であるから，特に区間 [0,1) における不連続点の集合が高々可算個であることを示せばよい。

これを示そう。 f は広義単調増加であるから， a\in [0,1) に対し，

f(a-) = \lim_{x \to a-0} f(x), \quad f(a+) = \lim_{x \to a+0} f(x)

が存在する。これを用いると， f の区間 [0,1) における不連続点の集合 A は

A = \{ a \in [0,1) \mid f(a+) - f(a-) > 0\}

と表せる。ここで，

 A_n = \left\{ a \in [0,1) \mid f(a+) - f(a-) > \tfrac{f(1)-f(0)}{n}\right\}

と定めると， f は単調であるから，集合A_nの個数について，

\#A_n \le n

とならねばならない。すなわち A_n は有限集合。
A = \bigcup_{n=1}^\infty A_n であるから， A は高々可算集合であり，結論を得る。

証明終