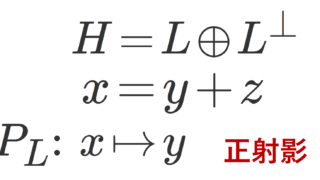グラムシュミットの直交化法 (Gram–Schmidt process),あるいは単にシュミットの直交化法とは,与えられた基底を用いて,正規直交基底を具体的に構成する手法です。グラムシュミットの直交化法について,その手法とイメージの図解を紹介します。
グラムシュミットの直交化法とは
本記事では, \langle \boldsymbol{a},\boldsymbol{b}\rangle で \boldsymbol{a} と \boldsymbol{b} の内積を表します。
グラムシュミットの直交化法
V を内積空間とし, \{\boldsymbol{a_n}\}\subset V をその基底とする。このとき,n=1,2,3,\dots に対し,
\color{red} \boldsymbol{x_n}=\boldsymbol{a_n}-\sum_{k=1}^{n-1} \langle \boldsymbol{a_n}, \boldsymbol{e_k}\rangle \boldsymbol{e_k}, \quad \boldsymbol{e_n}=\frac{\boldsymbol{x_n}}{\|\boldsymbol{x_n}\|}
で構成される \{e_n\} は正規直交基底となる。ただし, \sum_{k=1}^0 = 0 と解釈する。
n=1,2,3,\dots を具体的に書いてみると,
\small \begin{aligned}\boldsymbol{x_1} &= \boldsymbol{a_1} & \boldsymbol{e_1}&=\frac{\boldsymbol{x_1}}{\|\boldsymbol{x_1}\|} \\ \boldsymbol{x_2} &= \boldsymbol{a_2}-\langle\boldsymbol{a_2},\boldsymbol{e_1} \rangle \boldsymbol{e_1} & \boldsymbol{e_2}&=\frac{\boldsymbol{x_2}}{\|\boldsymbol{x_2}\|}\\ \boldsymbol{x_3} &= \boldsymbol{a_3}-\bigl\{\langle\boldsymbol{a_3},\boldsymbol{e_1} \rangle \boldsymbol{e_1}+\langle\boldsymbol{a_3},\boldsymbol{e_2} \rangle \boldsymbol{e_2} \bigr\}& \boldsymbol{e_3}&=\frac{\boldsymbol{x_3}}{\|\boldsymbol{x_2}\|}\\ &\quad \vdots \end{aligned}
という感じです。\boldsymbol{e_1} を使って \boldsymbol{e_2} を,\boldsymbol{e_1},\boldsymbol{e_2} を使って \boldsymbol{e_3} を帰納的に定義していますね。
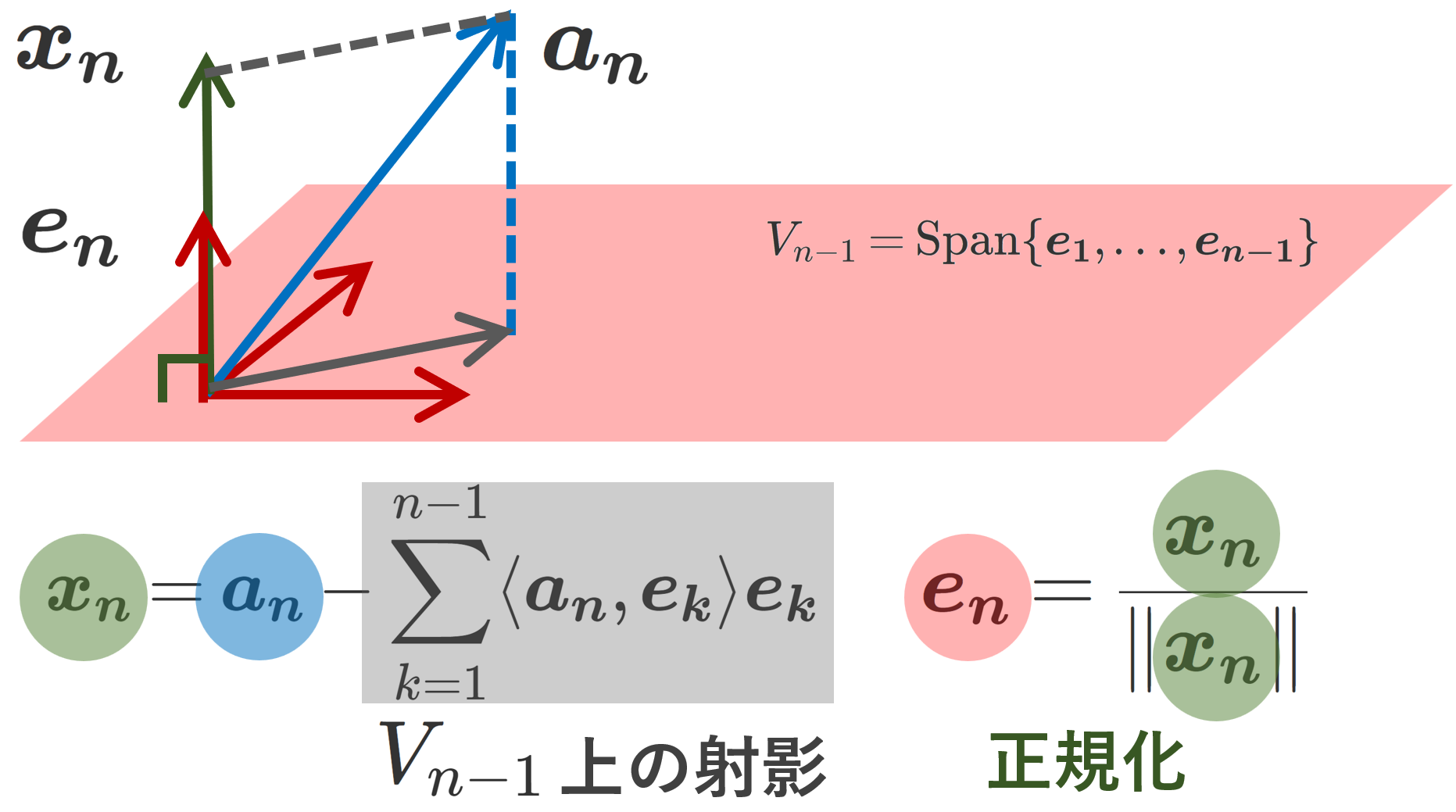
式の構造は,以下の図のようになっています。
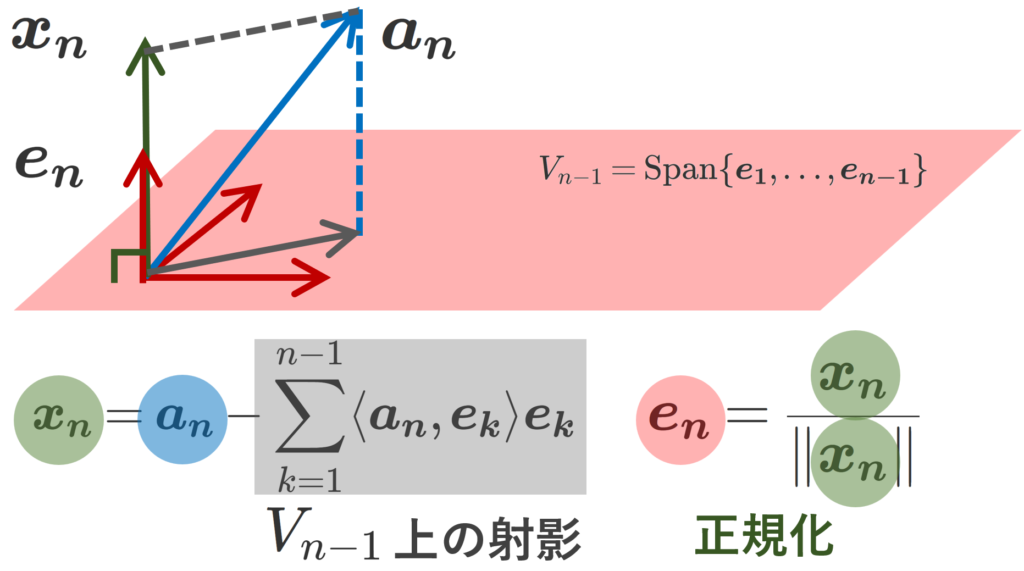
上の図は厳密には n=3 の例です。まず,灰色 \sum_{k=1}^{n-1} \langle \boldsymbol{a_n}, \boldsymbol{e_k}\rangle \boldsymbol{e_k} の部分は, \boldsymbol{a_n} を \boldsymbol{e_1},\dots, \boldsymbol{e_{n-1}} が張る空間 V_{n-1}=\operatorname{Span}\{\boldsymbol{e_1},\dots, \boldsymbol{e_{n-1}}\} への正射影したものです。この正射影を \boldsymbol{a_n} から引いた \boldsymbol{x_n} は, V_{n-1} と垂直になります。
この \boldsymbol{x_n} をノルム(大きさ)が 1 になるよう正規化してあげることで,正規直交基底の一つとなる \boldsymbol{e_n} が得られるわけです。
\{\boldsymbol{e_n}\} が正規直交基底になっていることを簡単に証明しておきましょう。
\{\boldsymbol{e_n}\} が正規直交基底である証明
\|\boldsymbol{e_n}\|=1 は明らかなので,上の手順で構成した \boldsymbol{e_n} が \boldsymbol{e_1}, \boldsymbol{e_2}, \dots, \boldsymbol{e_{n-1}} と垂直であることを示せばよい。
数学的帰納法で示す。 \boldsymbol{e_1}, \boldsymbol{e_2}, \dots, \boldsymbol{e_{n-1}} が互いに垂直であるとする。
このとき, 1\le i\le n-1 に対し,
\begin{aligned} \langle\boldsymbol{x_n},\boldsymbol{e_i} \rangle &= \left\langle\boldsymbol{a_n}-\sum_{k=1}^{n-1} \langle \boldsymbol{a_n}, \boldsymbol{e_k}\rangle \boldsymbol{e_k},\boldsymbol{e_i} \right\rangle \\ &= \langle\boldsymbol{a_n},\boldsymbol{e_i}\rangle -\sum_{k=1}^{n-1} \langle \boldsymbol{a_n}, \boldsymbol{e_k}\rangle \langle\boldsymbol{e_k},\boldsymbol{e_i} \rangle \\ &= \langle\boldsymbol{a_n},\boldsymbol{e_i}\rangle-\langle\boldsymbol{a_n},\boldsymbol{e_i}\rangle \\ &= 0 \end{aligned}
である。よって, \boldsymbol{x_n} が \boldsymbol{e_1}, \boldsymbol{e_2}, \dots, \boldsymbol{e_{n-1}} と垂直であるので, \boldsymbol{e_n}=\frac{\boldsymbol{x_n}}{\|\boldsymbol{x_n}\|} が \boldsymbol{e_1}, \boldsymbol{e_2}, \dots, \boldsymbol{e_{n-1}} と垂直であることが示せた。
証明終
元の基底と直交化した基底の関係
ほぼ自明かもしれませんが,以下の定理が成立します。
定理(元の基底と直交化した基底の関係)
- \boldsymbol{e_n} は \boldsymbol{a_1}, \boldsymbol{a_2}, \dots, \boldsymbol{a_n} の一次結合(線形結合)でかける。
- \boldsymbol{a_n} は \boldsymbol{e_1}, \boldsymbol{e_2}, \dots, \boldsymbol{e_n} の一次結合(線形結合)でかける
特に, \color{red}\operatorname{Span}\{\boldsymbol{a_1},\dots, \boldsymbol{a_{n}}\}=\operatorname{Span}\{\boldsymbol{e_1},\dots, \boldsymbol{e_{n}}\} です(Spanの意味とは【線形結合】)。
証明
1.について \boldsymbol{e_n} を構成する式を考えると, \boldsymbol{a_{1}},\dots, \boldsymbol{a_{n}} のみが関わっていて,\boldsymbol{a_{n+1}},\boldsymbol{a_{n+2}},\dots は出現しないため,いえる。
2.について \boldsymbol{x_n} を構成する式より,
\boldsymbol{a_n} = \boldsymbol{x_n}+\sum_{k=1}^{n-1} \langle \boldsymbol{a_n}, \boldsymbol{e_k}\rangle \boldsymbol{e_k}
であり,さらに \boldsymbol{x_n} = \langle\boldsymbol{a_n}, \boldsymbol{e_n} \rangle\boldsymbol{e_n} なので,
となるため,示せた。
証明終