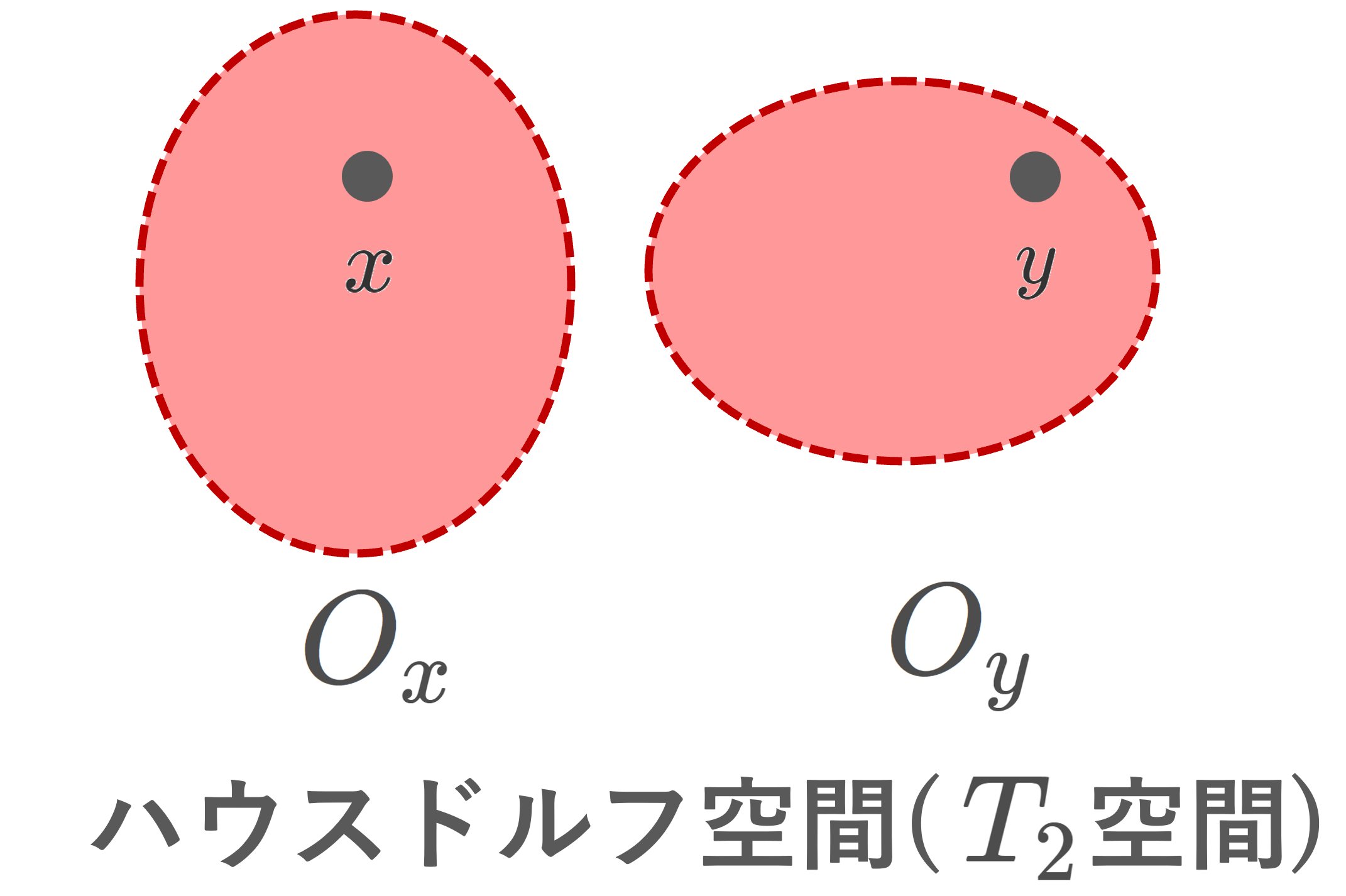
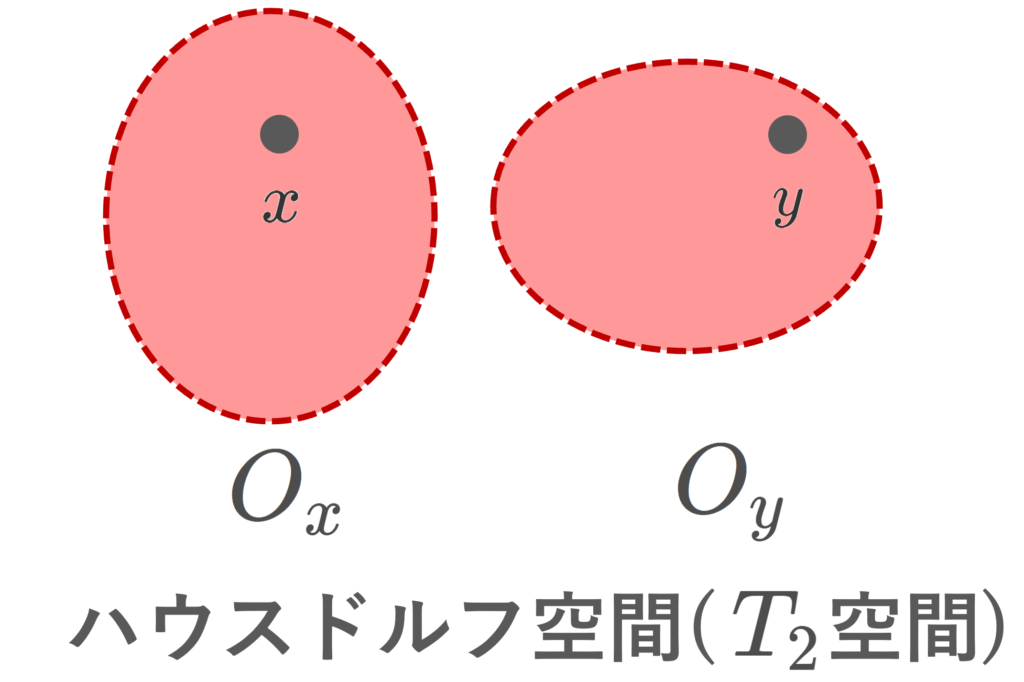
ハウスドルフ空間( T_2 空間)とは,任意の異なる2点が,開集合によって分離される空間のことをいいます。言い換えると,2点の開近傍で,共通部分をもたないものを取ってこれるということです。ハウスドルフ空間は,距離空間や位相多様体・関数解析における弱位相など,位相空間の応用上,最も成り立つ性質の一つと言えます。
ハウスドルフ空間についての定義・具体例・性質を詳しく紹介しましょう。
ハウスドルフ空間(T2空間)の定義
定義(ハウスドルフ空間・ T_2 空間)
(X,\mathcal{O}) を位相空間とする。任意の異なる2点 x,y\in X に対し,開集合 O_x, O_y\in\mathcal{O} が存在して,
\Large\color{red} x\in O_x, \; y\in O_y,\; O_x\cap O_y=\emptyset
が成り立つとき, (X,\mathcal{O}) をハウスドルフ空間 (Hausdorff space) または T_2 空間 ( T_2 space) という。
このような状況を, x,y は開集合で分離される (separated by open sets) といいます。
なお,ハウスドルフよりさらに弱めて,
x\in O_x かつ y \notin O_x となる O_x\in\mathcal{O}
x\notin O_y かつ y \in O_y となる O_y\in\mathcal{O}
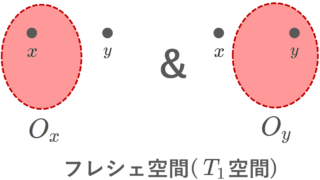
のうち,少なくとも一方が成立するような空間を T_0 空間 ( T_0 space) またはコルモゴロフ空間 (Kolmogorov space) といい(→【位相空間】コルモゴロフ空間(T0空間)の定義と具体例),両方が成立するような空間を T_1 空間 ( T_1 space) といいます。

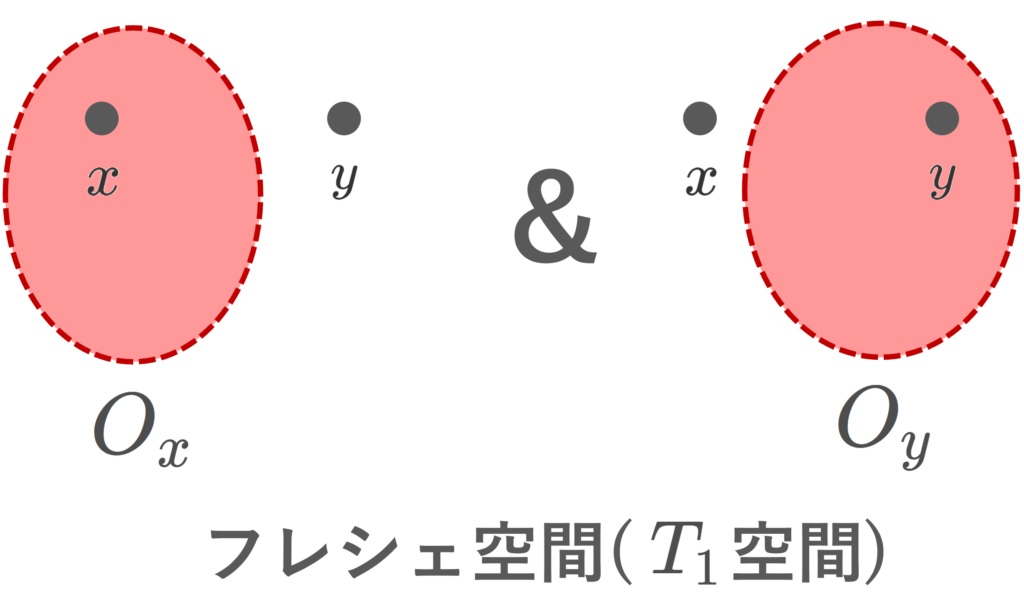
明らかに T_2\implies T_1\implies T_0 です。あとで, T_1 だが T_2 でない例も紹介しましょう。
それ以外の分離公理もまとめておきます。定義は文献[1]に依っています。
| 名称 | 定義 |
|---|---|
| T_0 コルモゴロフ | 任意の異なる2点 x,y\in X に対して, x\in O_x,\, y\notin O_x となる開集合 O_x または x\notin O_y,\, y\in O_y となる開集合 O_y の少なくとも一方が取れる |
| T_1 | 任意の異なる2点 x,y\in X に対して, x\in O_x,\, y\notin O_x となる開集合 O_x と x\notin O_y, \,y\in O_y となる開集合 O_y の両方が取れる |
| T_2 ハウスドルフ | 任意の異なる2点 x,y\in X が開集合で分離される, すなわち x\in O_x, \, y\in O_y,\, O_x\cap O_y=\emptyset となる開集合 O_x, O_y が取れる |
| T_{2 \frac {1}{2}} 完全ハウスドルフ | 任意の異なる2点 x,y\in X が閉近傍で分離される, すなわち x\in O_x, \, y\in O_y,\, \overline{O_x}\cap \overline{O_y}=\emptyset となる開集合 O_x, O_y が取れる |
| ウリゾーン | 任意の異なる2点 x,y\in X が連続関数で分離される, すなわち連続関数 f\colon X\to [0,1] で, f(x)=0,\, f(y)=1 となるものが取れる ※ ウリゾーンと T_{2\frac{1}{2}}(完全ハウスドルフ)の定義を逆にすることがある |
| T_3 | 任意の閉集合 F と任意の点 x\in X\setminus F が開集合で分離される, すなわち F\subset O_F,\, x\in O_x,\, O_F\cap O_x=\emptyset となる開集合 O_F, O_x が取れる |
| 正則 (regular) | T_0 かつ T_3( \iff T_2 かつ T_3) ※ 正則と T_3 の定義を逆にすることがある |
| T_{3 \frac{1}{2}} | 任意の閉集合 F と任意の点 x\in X\setminus F が連続関数で分離される, すなわち連続関数 f\colon X\to [0,1] で, f|_F=0,\, f(x)=1 となるものが取れる |
| 完全正則・チコノフ | T_0 かつ T_{3 \frac{1}{2}}( \iff T_2 かつ T_{3 \frac{1}{2}}) |
| T_4 | 任意の2つの互いに素な閉集合 F,G\subset X が開集合で分離される, すなわち F\subset O_F,\, G\subset O_G,\, O_F\cap O_G=\emptyset となる開集合 O_F, O_G が取れる |
| perfectly T_4 | T_4 かつ任意の閉集合が G_\delta 集合である |
| 正規 (normal) | T_1 かつ T_4( \iff T_2 かつ T_4\iff T_3 かつ T_4) ※ 正規と T_4 の定義を逆にすることがある |
| T_5 | \overline{A}\cap B=A\cap \overline{B}=\emptyset をみたす任意の2つの集合 A,B\subset X が開集合で分離される, すなわち A\subset O_A,\, B\subset O_B,\, O_A\cap O_B=\emptyset となる開集合 O_A, O_B が取れる |
| completely 正規 | T_1 かつ T_5( \iff T_2 かつ T_5\iff T_3 かつ T_5) ※ completely 正規と T_5 の定義を逆にすることがある |
| T_6 perfectly 正規 | T_1 かつperfectly T_4 |
明らかに T_2\implies T_1\implies T_0 ですが,T_3, T_4, T_5 が成り立つからと言って, T_2(ハウスドルフ)が成り立つとは限りません。
ハウスドルフ空間の例・そうでない例
例1(\R).
実数全体の集合 \R はハウスドルフ( T_2)である。
異なる2点 x,y\in \R に対し, 0<\varepsilon<|x-y|/2 となるような \varepsilon を取ると,
(x-\varepsilon, x+\varepsilon)\cap(y-\varepsilon, y+\varepsilon)=\emptyset
となりますね。
x\in X,\, \varepsilon>0 に対し, x の \varepsilon -近傍を
B_\varepsilon (x)= \{ y\in X\mid d(x,y)<\varepsilon\}
としましょう。任意の異なる x,y に対し, k=d(x,y) とおくと, B_{k/2}(x), B_{k/2}(y) によって, x と y は開集合で分離できていますね。
例3(離散位相).
(X,2^X) を離散空間とすると,これはハウスドルフ( T_2)である。
任意の異なる x,y に対し, \{x\}, \{y\} は開集合なので,これで分離できています。
例4(密着位相).
(X, \{\emptyset, X\}) を密着空間とする。このとき, X が1点集合のときはハウスドルフであるが, X が2点以上の集合のときはハウスドルフ( T_2)でない。 T_1 でも T_0 でもない。
1点集合のときにハウスドルフなのは,そもそも異なる2点が取れないからです。これは空虚な真 (vacuous truth) です。
例5(補有限位相).
X を無限集合とし,
\mathcal{O}=\{ O\subset X\mid X\setminus O \text{ is finite}\}\cup\{\emptyset\}
を,補集合が有限集合である部分集合全体とすると, (X,\mathcal{O}) は位相空間である。この空間は T_1 であるが,ハウスドルフ( T_2)ではない。
x,y\in X を,異なる2点とします。 X\setminus \{x\}, X\setminus \{y\} はどちらも開集合で,それぞれ x,y の一方を含み,もう一方を含まないので, T_1 の定義を満たしています。
一方で,ハウスドルフ( T_2)と仮定すると,開集合 O_x, O_y\in\mathcal{O} を, x\in O_x,\, y\in \mathcal{O}_y,\, O_x\cap O_y=\emptyset となるように取れます。ここで, (X\setminus O_x)\cup(X\setminus O_y) = X ですから, X\setminus O_x,X\setminus O_y の少なくとも一方は無限集合になります。これは,補集合が有限集合であることに矛盾していますね。
補有限位相は,以下でも解説しています。
例6.
通常の位相が入った \R と,離散空間 \{ 0,1\} の積空間である,2つの数直線 \widehat{X}=\R\times \{0,1\} に対し,同値関係
(t, 0)\sim (t,1) \quad t<0
による商空間 X=\widehat{X}/\sim を考えると,この空間は T_1 であるが,ハウスドルフ( T_2)ではない。
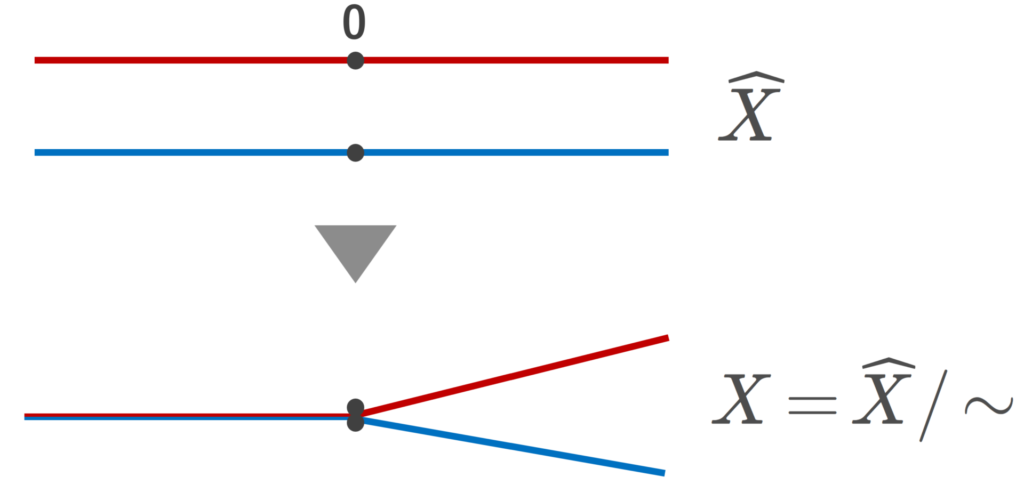
(0,0)\in X を含む開集合と (0,1)\in X を含む開集合は必ず共通部分を持ってしまうので,ハウスドルフ( T_2)ではありません。
あまり例を挙げすぎるのもアレなので,本サイトの別ページで紹介しているもので,面白いものを並べておきます。興味あればリンク先にアクセスしてみてください。
| 例 | 分離公理 |
|---|---|
| シェルピンスキー空間 | T_0, T_4, T_5 だが T_1,T_2,T_3 でない |
| K位相(スミルノフ位相) | T_0, T_1, T_2 だが T_3,T_4,T_5 でない |
| ゾルゲンフライ平面 | T_0, T_1, T_2, T_3 だが T_4,T_5 でない |
もっと例も増やしていきたいと思っています。
ハウスドルフ空間の性質
の順に,証明付きで紹介しましょう。
1. ハウスドルフ空間の同値な性質
定理1(ハウスドルフ空間の同値な性質)
(X, \mathcal{O}) を位相空間とする。このとき,以下は同値である。
- X はハウスドルフ( T_2)である
- 異なる任意の x,y\in X に対し, x\in O かつ y\notin \overline{O} となる開集合 O\in\mathcal{O} が存在する
- 直積 X\times X における対角線集合 (diagonal set) \Delta =\{ (x,x)\mid x\in X\} が閉集合である
- 任意の x\in X に対し, x の閉近傍全体を \mathcal{F}(x) とすると, \bigcap_{F\in\mathcal{F}(x)} F = \{x\} となる
- X における任意のネット(有向点族)収束先は高々一つである
- X における任意のフィルターの収束先は高々一つである
4.はただの閉集合ではなく,閉近傍であることに注意してください。たとえば, \R において, \{x\} は x を含む閉集合ですが, x の閉近傍ではありません。
地道に証明しましょう。
証明
1.\implies 2.について
x,y\in X を異なる2点とする。 X はハウスドルフより, x\in O_x, \, y\in O_y,\, O_x\cap O_y=\emptyset となる開集合 O_x, O_y\in\mathcal{O} が取れる。このとき, y\in O_y \subset X\setminus O_x であり, O_y は開集合で X\setminus O_x に含まれる最小の開集合は X\setminus \overline{O_x} なので, y\in X\setminus \overline{O_x} すなわち y\notin \overline{O_x} となる。
2.\implies 1.について
2.の仮定において, O_x=O, \, O_y=X\setminus \overline{O} とすればよい。
1.\implies 3.について
x,y\in X を異なる2点とする。 X はハウスドルフより, x\in O_x, \, y\in O_y,\, O_x\cap O_y=\emptyset となる開集合 O_x, O_y\in\mathcal{O} が取れる。このとき, (x,y)\in O_x\times O_y であり, O_x\times O_y\subset X\times X は \Delta と共通部分をもたない開集合である。
任意の (x,y)\in (X\times X)\setminus \Delta が \Delta と共通部分をもたない開近傍をもつので, \Delta が閉集合であることが示せた。
3.\implies 1.について
\Delta\subset X\times X は閉集合なので,任意の (x,y)\in (X\times X)\setminus \Delta が \Delta と共通部分をもたない開近傍をもつ。直積位相の定義より, (x,y)\in U\times V\subset (X\times X)\setminus \Delta となる X の開集合 U, V\in \mathcal{O} が存在する。
ここで, x\in U, \, y\in V,\, U\cap V=\emptyset であるから,X はハウスドルフである。
1.\implies 4.について
x\in X とする。X はハウスドルフより,異なる y\ne x に対し, x\in O_x, \, y\in O_y,\, O_x\cap O_y=\emptyset となる開集合 O_x, O_y\in\mathcal{O} が取れる。このとき, x\in O_x\subset X\setminus O_y であるから, X\setminus O_y\in \mathcal{F}(x) である。
x\in\bigcup_{F\in\mathcal{F}(x)} F\subset \bigcup_{y\ne x} X\setminus O_y = \{x\}
であるから,題意は示された。
4.\implies 1.について
x,y\in X を異なる2点とする。4.の仮定より,ある F\in\mathcal{F}(x) が存在して, y\notin F とできる。 F は x の閉近傍なので, x\in U\subset F となる U\in\mathcal{O} が存在する。このとき, U, X\setminus F は開集合であり,
x\in U, \, y\in X\setminus F,\, U\cap(X\setminus F)=\emptyset
となるから, x と y は開集合で分離される。よって, X はハウスドルフである。
1.\iff 5.については,ネット(有向点族)による位相空間論と点列との比較で証明している。
1.\iff 6.については,位相空間におけるフィルターの概念を詳しくで証明している。
証明終
2. ハウスドルフ空間のその他の性質
なお他にも,ハウスドルフ空間( T_2 空間)における1点集合 \{x\} は常に閉集合です。1点集合が閉集合であることは, T_1 空間であることと同値です(→【位相空間】T1空間の定義・具体例と性質)。また, T_1 であることは,定理1の4.の閉近傍を(開)近傍 \mathcal{N}(x) に変えて \bigcap_{N\in\mathcal{N}(x)} N = \{x\} となることとも同値です(→【位相空間】T1空間の定義・具体例と性質)。
また, T_1 空間(したがって,ハウスドルフ空間)においては,T_4\implies T_3 (正規 \implies 正則)になります。これは,1点集合が閉集合になることから直ちにわかります。
1.については, 相対位相と部分位相空間の定義・具体例5つ・性質5つ内で証明しています。2.については,直積位相とは~定義・具体例・性質~内で証明しています。3.については,前述の例6.または商位相と商写像内で紹介しています。
3. ハウスドルフ空間と連続写像の性質
定理3(ハウスドルフ空間と連続写像の性質)
(X, \mathcal{O}_X), (Y,\mathcal{O}_Y) を位相空間とし, f,g\colon X\to Y とする。
2.については,タイトルと異なって別に連続写像でなくても構いません。
4.が面白い性質で,2つの連続写像が一致するかどうかを見たければ,稠密な部分集合上のみで見ればよい,と言っています。稠密な集合のみで考えるのが分かりやすい場面は,応用上たくさんありますから,有用です。
証明
以下で, A=\{(x_1,x_2)\mid f(x_1)=f(x_2)\} とする。
1.について
(x_1,x_2)\in (X\times X)\setminus A とする。このとき, f(x_1)\ne f(x_2) と, Y がハウスドルフであることより, f(x_1)\in V_1, \, f(x_2)\in V_2,\, V_1\cap V_2=\emptyset となる V_1, V_2\in\mathcal{O}_Y が取れる。
f は連続より, f^{-1}(V_1), f^{-1}(V_2)\in\mathcal{O}_X であり, f^{-1}(V_1), f^{-1}(V_2) はそれぞれ x_1,x_2 の開近傍である。したがって, f^{-1}(V_1)\times f^{-1}(V_2) は X\times X の (x_1,x_2) における開近傍であり, V_1\cap V_2=\emptyset から f^{-1}(V_1)\times f^{-1}(V_2)\subset (X\times X)\setminus A となる。
任意の (x_1,x_2)\in (X\times X)\setminus A が (X\times X)\setminus A に含まれる開近傍をもつので, A は閉集合である。
2.について
y_1, y_2\in Y を異なる2点とする。 f は全射より, x_1, x_2\in X が存在して,y_1= f(x_1),\, y_2= f(x_2) とできる。このとき, (x_1, x_2)\in (X\times X)\setminus A である。 A は閉集合であることと,直積位相の定義より, x_1, x_2 の開近傍 U_1, U_2\in\mathcal{O}_X で,
(x_1, x_2)\in U_1\times U_2 \subset (X\times X)\setminus A
となるものが取れる。 f は開写像なので, f(U_1), f(U_2) はそれぞれ f(x_1),f(x_2) の開近傍であり, f(U_1)\cap f(U_2)=\emptyset である(そうでないと (U_1\times U_2)\cap A=\emptyset に矛盾する)から, Y はハウスドルフである。
3.について
H=\{ x\in X\mid f(x)=g(x)\} とおく。 x\in X\setminus H とすると, f(x)\ne g(x) であることと, Y がハウスドルフであることより, f(x), g(x) の開近傍 V_1 , V_2\in\mathcal{O}_Y で, V_1\cap V_2=\emptyset となるものが取れる。
f,g は連続より, f^{-1}(V_1), g^{-1}(V_2) はともに x の開近傍であるから, f^{-1}(V_1)\cap g^{-1}(V_2) も x の開近傍である。
x\in f^{-1}(V_1)\cap g^{-1}(V_2)\subset X\setminus H
であるから, x は X\setminus H に含まれる開近傍をもつ。よって, H は閉集合である。
4.については,3.と,稠密の定義よりほぼ明らか。
証明終
1,3.の証明については,ネット(有向点族)の知識があればもっと明快です。例えば,1.については,ネット(有向点族) \bigl((x^{(1)}_\lambda, x^{(2)}_\lambda)\bigr)\subset X\times X が (x^{(1)}_\lambda, x^{(2)}_\lambda)\to (x^{(1)}, x^{(2)}) かつ f(x^{(1)}_\lambda)=g(x^{(2)}_\lambda) をみたすならば, f(x^{(1)})=g(x^{(2)}) ですね。
なお, X がハウスドルフでもその連続写像の像 f(X) がハウスドルフとは限りません。たとえば,離散空間から密着空間への写像は常に連続ですが,その像はハウスドルフとは限りません。
ハウスドルフ性とコンパクト性
ハウスドルフという性質は,位相が大きい(強い・細かい)ほど成り立ちやすい性質です。逆に,コンパクトという性質は,位相が小さい(弱い・粗い)ほど成り立ちやすい性質です。よって,コンパクトハウスドルフ空間は,絶妙に位相の大きさが程よく,奇跡の空間です。そんな,ハウスドルフ性とコンパクト性の関連について述べた定理を紹介しましょう。
定理4(ハウスドルフ性とコンパクト性)
- ハウスドルフ空間のコンパクト集合は閉集合である
- コンパクト空間からハウスドルフ空間への全単射連続写像は同相写像である
- ハウスドルフ空間において,共通部分をもたない2つのコンパクト集合は,開集合によって分離される
すなわち, K\cap L=\emptyset となるコンパクト集合 K,L について, K\subset U, \, L\subset V,\, U\cap V=\emptyset となる開集合 U,V が存在する。特に,コンパクトハウスドルフ空間は正規( T_4)である。 - パラコンパクトハウスドルフ空間は正規( T_4)である。
- 局所コンパクトハウスドルフ空間は正則( T_3)である。ただし,局所コンパクトとは,任意の点に対し,その点の近傍でコンパクトなものが存在することをいう。
定理2.1より,ハウスドルフ空間におけるコンパクト集合は部分空間としてコンパクトハウスドルフ空間です。
1.については,コンパクト空間とコンパクト集合について詳しくで証明しています。2.については,同相写像と同相(位相同型)の定義・具体例・性質で証明しています。2.の性質はかなり強い性質ですね。
3,4,5.の証明
3.について
(X,\mathcal{O}) をハウスドルフ空間とする。まず,コンパクト集合 K\subset X と,任意の x\in X\setminus K が開集合によって分離されることを示す。 \mathcal{C}=\{ O\in \mathcal{O}\mid x\notin \overline{O}\} は K の開被覆になる。なぜなら, X はハウスドルフより,定理1の1.\iff2.から各点 a\in K に対し, a\in O かつ x\notin \overline{O} となる O\in\mathcal{O} が存在するからである。
K はコンパクトなので,有限個の集合 C_1,C_2,\ldots, C_m\in\mathcal{C} が存在して,
K\subset C_1\cup C_2\cup \cdots\cup C_m
とできる。右辺を C とすると,【位相空間】閉包とは~定義と例と性質~より,
となる。右辺は x を含まないので,x\notin \overline{C} となる。これと K\subset C と,定理1の2.\implies 1.と同様の議論により,緑字が示せる。
次に3.の主張を示す。 K,L\subset X をコンパクト集合で, K\cap L=\emptyset をみたすとする。ここまでの議論より,\mathcal{D}=\{ O\in\mathcal{O}\mid \overline{O}\cap K=\emptyset\} は L の開被覆になる。L はコンパクトだから,有限個の集合 D_1, D_2,\ldots, D_n\in\mathcal{D} が存在して,
L\subset D_1\cup D_2\cup \cdots \cup D_n
とできる。右辺を D とすると, D は開集合であり,また【位相空間】閉包とは~定義と例と性質~より,
となる。\overline{D}\cap K=\emptyset である。定理1の2.\implies 1.と同様の議論により,定理の前半の主張が従う。また,コンパクト空間における閉集合は常にコンパクトなので,後半も従う。
4.について
3.について,「有限部分被覆が存在」の議論をしている部分を,「局所有限な開細分被覆が存在」の議論に置き換えると,【位相空間】閉包とは~定義と例と性質~が同じように使えて,ほぼ同様に証明できる。
5.について
F\subset X を閉集合とし, x\in X\setminus F とする。 X は局所コンパクトであることと1.より, x の開近傍 S で, \overline{S} がコンパクトなものが存在する。\overline{S}\cap F は閉集合であることと,コンパクト空間の閉部分集合はコンパクトなので,\overline{S}\cap F は x を含まないコンパクト集合である。
3.の前半の証明より, x と \overline{S}\cap F は開集合 U, V によって分離できる。特に定理1の1. \implies 2.の議論より, x\in U かつ \overline{S}\cap F\cap\overline{U}=\emptyset とできる。
S\cap U は開集合であり,一般に, \overline{A\cap B}\subset \overline{A}\cap \overline{B} (→【位相空間】閉包とは~定義と例と性質~)なので,
x\in S\cap U,\quad F\cap \overline{S\cap U} \subset \overline{S}\cap F\cap\overline{U}=\emptyset
となるので,定理1の2.\implies 1.と同様の議論により,示せる。
証明終
3.の証明は,有限個の和集合の閉包は,閉包の有限個の和集合と一致することがカギになっています。4.もそれと似ています。