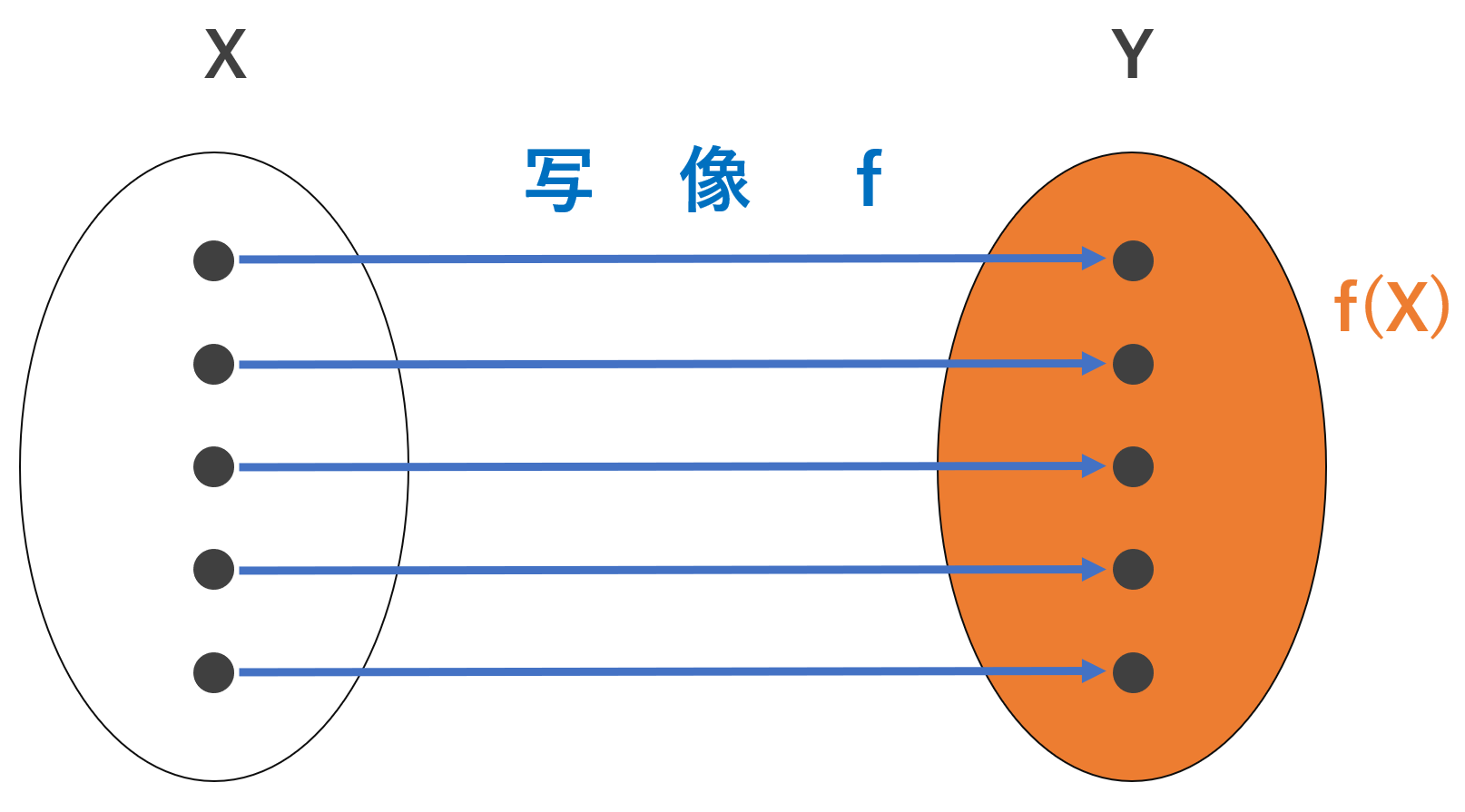
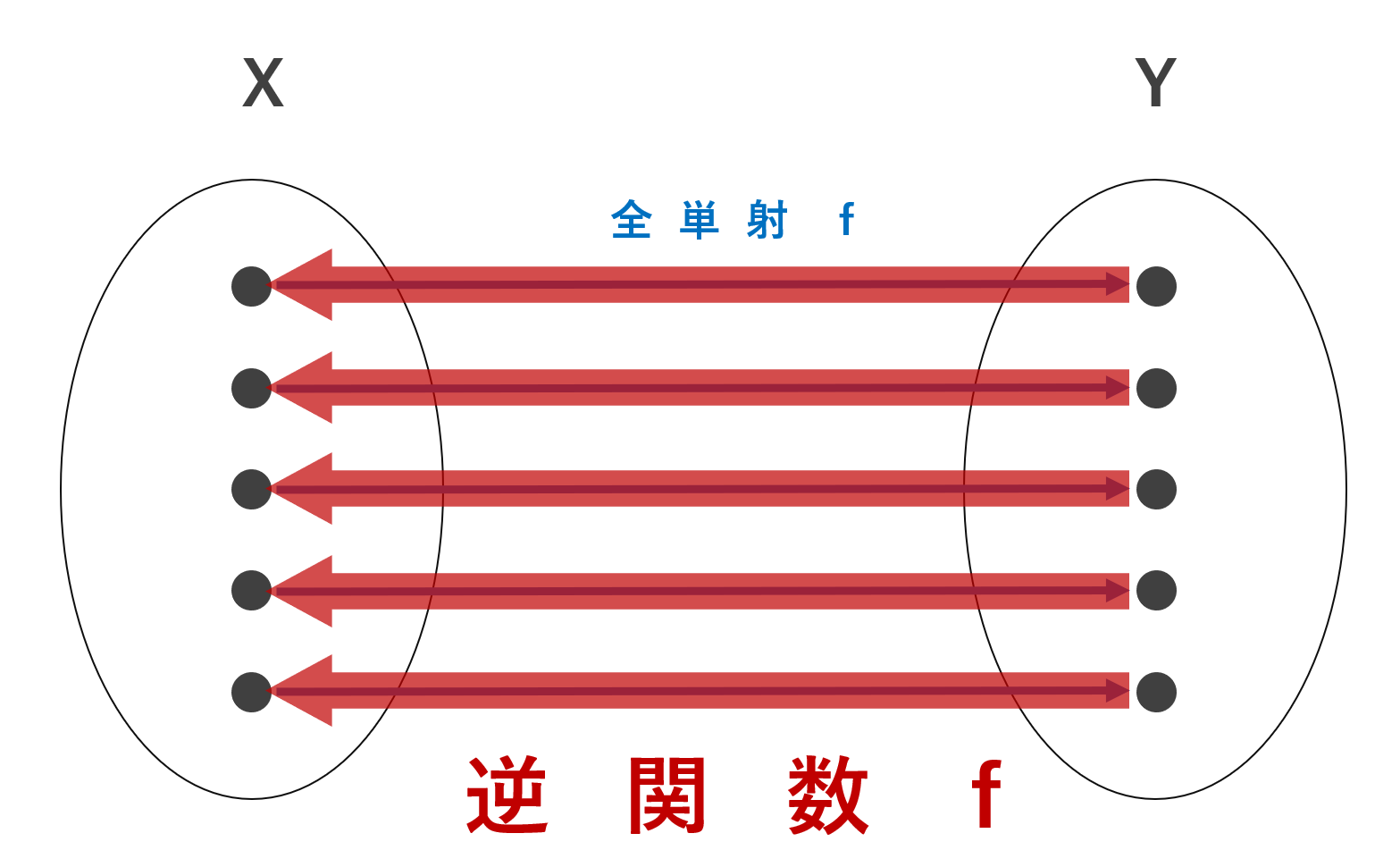
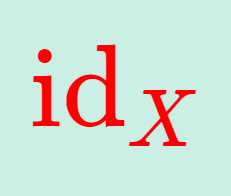恒等写像・包含写像とは，ともに f(x)=x となるような写像で，恒等写像は定義域と終域が同じもの，包含写像は終域が定義域よりも大きいものを指します。これについて，詳しく解説します。
恒等写像・包含写像の定義
恒等写像の定義
定義（恒等写像）
f\colon X \to X が， f(x) = x をみたすとき，これを恒等写像 (identity map, identity function) という。
恒等写像を \textcolor{red}{\mathrm{id}} や，集合を明示して \textcolor{red}{\mathrm{id}_X} などとかく。
定義域と終域が同じであり，かつ各要素を自分自身にうつす写像を恒等写像というんですね。
包含写像の定義
定義（包含写像）
X \subset Y とし， \iota \colon X \to Y が \iota(x) = x をみたすとき，これを包含写像 (inclusion map, inclusion function) という。
包含写像は特に慣例的な書き方はないが，ギリシャ文字の「イオタ」である \textcolor{red}{\iota} やアルファベットの「アイ」である \textcolor{red}{i} はしばしば使われる。
恒等写像は定義域と終域が同じであったのに対し，包含写像では終域が定義域より広いということですね。
恒等写像・包含写像の性質
明らかに，以下のような性質が成立します。
なお，ここからは全射・単射・全単射，合成写像，逆写像については既知とします。
恒等写像の性質
命題（恒等写像の性質）
- \mathrm{id} は全単射でありかつ \mathrm{id}^{-1} = \mathrm{id} である。
- f\colon X \to Y とするとき，f \circ \mathrm{id}_X = \mathrm{id}_Y \circ f = f である。
包含写像の性質
命題（包含写像の性質）
- 包含写像は単射である。
- f\colon X \to Y に対し，定義域を A \subset X に制限した写像は，包含写像 \iota\colon A \to X を用いて f \circ \iota \colon A \to Y とかける。
ここで，包含写像は単射であるため， \iota \colon X \hookrightarrow Y とかけます。 「 X \subset Y の包含関係」と「写像であること」をうまく一つで表したような矢印ですね。
また， X \subset Y でなくても， \iota\colon X \to Y が単射であり，数学的に X が Y の部分集合とみなせる(たとえば演算規則が保存されるなどの)場合は， \iota を包含写像とみなすことで， X \subset Y とみなす場合があります。
