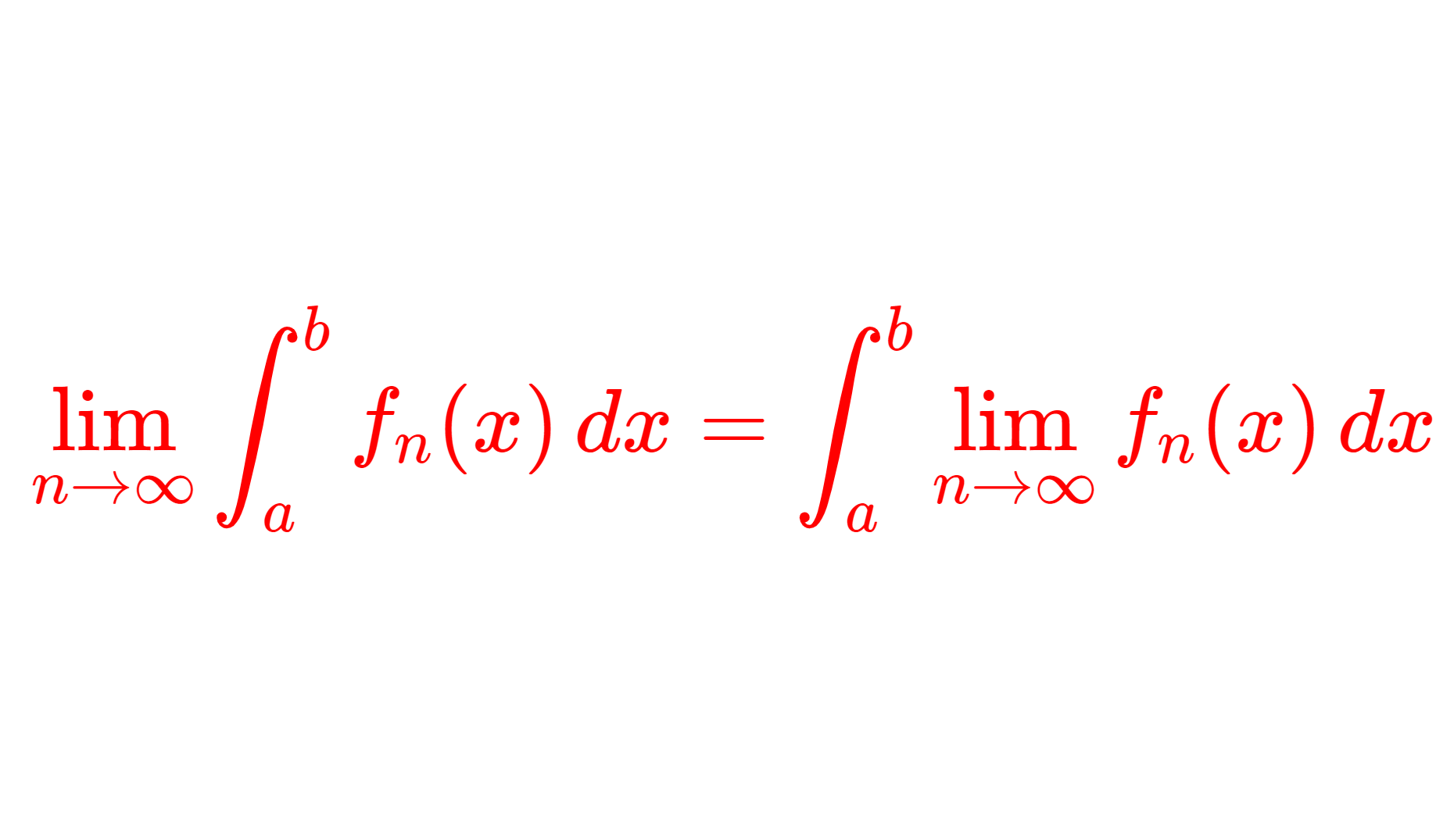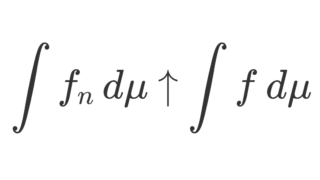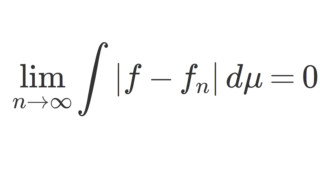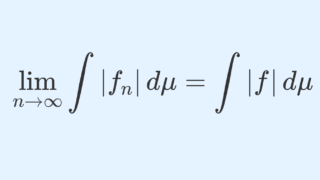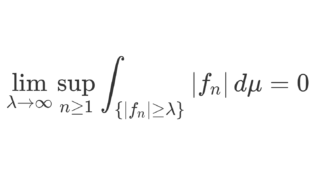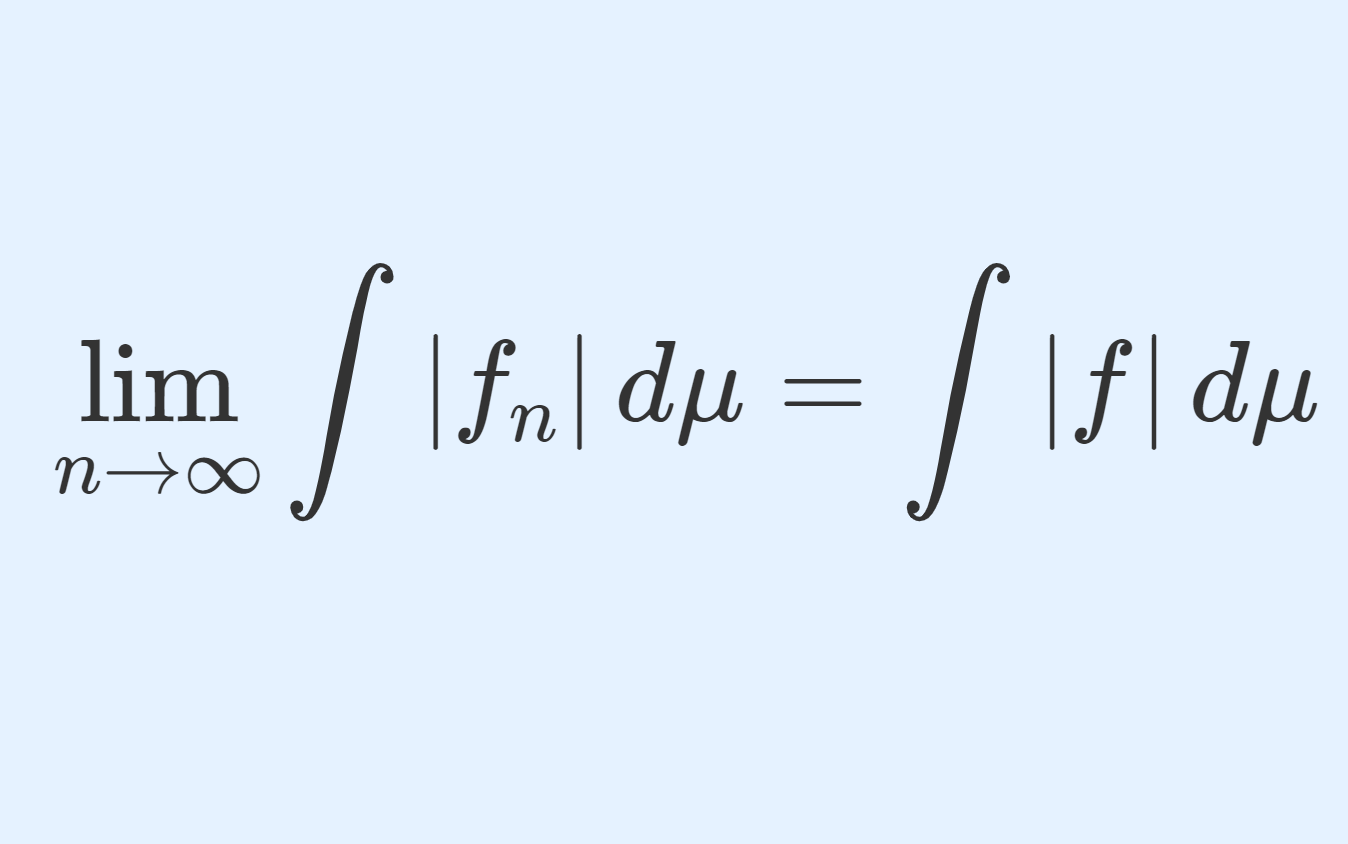極限と積分の順序交換定理6つの主張をまとめて紹介し,さらに極限と積分が交換できない例についても述べましょう。
本記事はまとめ記事とし,実際の証明などは定理の主張下にあるリンク先を見てください。
極限と積分の順序交換定理
以下,考える関数は全て実数 \mathbb{R} を定義域・終域とし,積分が意味を持つ ( \pm\infty でもよい) とします。さらに積分範囲 \int_a^b について, -\infty \le a<b\le \infty のときは \int_{-\infty}^\infty でもよいとします。
すべての定理は,各点で f(x)=\lim_{n\to\infty} f_n(x) (各点収束)を仮定とし,結論の式が
\lim_{n\to\infty} \int_a^b f_n(x)\,dx = \int_a^bf(x)\,dx
です。これは言い換えると,
ですから,極限と積分の交換定理ですね。なお, g_n=f_n-f_{n-1} (ただし f_0\equiv 0)とすると,
ですから,和と積分の交換定理(項別積分)にも応用可能です。
単調収束定理
定理1(単調収束定理)
-\infty\le a< b\le \infty とする。
\{f_n\} は各点 x\in (a,b) で 0\le f_1(x)\le f_2(x)\le f_3(x)\le \cdots かつ f(x)=\lim_{n\to\infty} f_n(x) (各点収束)とする。このとき,
\lim_{n\to\infty} \int_a^b f_n(x)\,dx = \int_a^bf(x)\,dx.結論の等式は \infty=\infty も許します。
関数列 \{f_n\} は非負かつ各点で単調増加であることが大切です。
有界収束定理
定理2(有界収束定理)
-\infty<a<b<\infty かつ M>0 は定数とする。
\{f_n\} は各 n\ge 1,\, x\in (a,b) で |f_n(x)| \le M であり, f(x)=\lim_{n\to\infty} f_n(x) (各点収束)とする。このとき,
\lim_{n\to\infty} \int_a^b f_n(x)\,dx = \int_a^bf(x)\,dx.積分範囲 (a,b) は有界であり,関数も n,x によらず有界であることが大切です。
これはルベーグの収束定理(優収束定理)の特別なバージョンですから,以下の中で解説しています。
ルベーグの収束定理(優収束定理)
定理3(ルベーグの収束定理)
-\infty\le a<b\le \infty かつ g(x)\ge 0 は \int_a^b g(x)\,dx<\infty をみたすとする。
\{f_n\} は各 n\ge 1,\, x\in (a,b) で |f_n(x)| \le g(x) であり, f(x)=\lim_{n\to\infty} f_n(x) (各点収束)とする。このとき,
\lim_{n\to\infty} \int_a^b f_n(x)\,dx = \int_a^bf(x)\,dx.上の定理2(有界収束定理)を一般化したのがこれです。積分区間は \int_{-\infty}^\infty でも構いませんが, n に依らず上から抑えるのが定数 M ではなく,可積分関数 g(x) です。
Schefféの補題
定理4(Schefféの補題)
-\infty\le a<b\le \infty とする。
\{f_n\} は各点 x\in (a,b) で f(x)=\lim_{n\to\infty} f_n(x) (各点収束)とし,さらに
\lim_{n\to\infty}\int_a^b |f_n(x)|\,dx=\int_a^b |f(x)|\,dx<\infty
とする。このとき,
絶対値をつけた状態で極限と積分を交換できるなら,絶対値を外しても極限と積分を交換可能だということですね。
ヴィタリの収束定理
定理5(ヴィタリの収束定理)
-\infty< a<b< \infty とする。
\{f_n\} は各点 x\in (a,b) で f(x)=\lim_{n\to\infty} f_n(x) (各点収束)とし,さらに
\lim_{\lambda\to\infty}\sup_{n\ge 1}\int_a^b |f_n(x)| 1_{\{ x\colon |f_n(x)|\ge \lambda\}}\,dx=0
とする( 1 は定義関数)(一様可積分という)。このとき,
積分区間 (a,b) が有界であることに注意してください。
一様収束と極限と積分の交換定理
最後に,大学1年生の微分積分学で習う極限と積分の交換定理を紹介しておきましょう。ルベーグの収束定理の特別なバージョンです。
定理6(一様収束と極限と積分の交換定理)
-\infty<a<b<\infty とする。
\{f_n\} は [a,b] 上連続関数列でかつ f に一様収束しているとする。このとき,
\lim_{n\to\infty} \int_a^b f_n(x)\,dx = \int_a^bf(x)\,dx.これは,ルベーグの収束定理(定理3)の特別なバージョンになっています。一様収束の確認が面倒なので,実際の専門数学でこの定理が使われることは少ないです。
極限と積分が交換できない例
極限と積分がいつでも交換できないことは既に知っていると思いますが,交換できない例を具体的に紹介しておきましょう。
極限と積分が交換できない例1.
f_n(x)=1_{[n,n+1]}(x) \left(= \begin{cases} 1 & n\le x\le n+1 ,\\ 0 & \text{otherwise}\end{cases}\right) とする。
このとき,各点で \lim_{n\to\infty} f_n(x)=0 であるが,
\begin{aligned}\lim_{n\to\infty}\int_0^\infty f_n(x)\,dx &= 1, \\ \int_0^\infty \lim_{n\to\infty}f_n(x) \,dx&= 0 \end{aligned}
となって,値が異なる。
f(x)>0 となる部分が x\to\infty に逃げていく場合です。
極限と積分が交換できない例2.
f_n(x)=n^2 1_{(0,1/n]}(x) \left(= \begin{cases} n^2 & 0< x\le 1/n ,\\ 0 & \text{otherwise}\end{cases}\right) とする。
このとき,各点 x\in (0, 1) で \lim_{n\to\infty} f_n(x)=0 であるが,
\begin{aligned}\lim_{n\to\infty}\int_0^1 f_n(x)\,dx & =\lim_{n\to\infty} n= \infty, \\ \int_0^1 \lim_{n\to\infty}f_n(x) \,dx&= 0 \end{aligned}
となって,値が異なる。
f(x)>0 となる x の範囲がどんどん小さくなっていく一方で, f(x)>0 の部分では f(x) の値がどんどん大きくなっていく場合です。
極限と積分が交換できない例3.
f_n \equiv -1/n とすると,各点で \lim_{n\to\infty} f_n(x)=0 であるが,
\begin{aligned}\lim_{n\to\infty}\int_0^\infty f_n(x)\,dx & =- \infty, \\ \int_0^\infty \lim_{n\to\infty}f_n(x) \,dx&= 0 \end{aligned}
となって,値が異なる。
f_n は単調増加に 0 に収束するが, f_n の積分はずっと -\infty のままの場合です。