一つのベクトル空間に対し,別の2つの基底を取ったときに,その関係性を述べる「基底の変換行列」について,その定義と性質を分かりやすく紹介します。「線形写像の表現行列」との比較も行います。
基底の変換行列とは
n 次元ベクトル空間の基底を \{ \boldsymbol{v_1}, \boldsymbol{v_2},\dots, \boldsymbol{v_n}\} としましょう。また,それとは別の基底 \{ \boldsymbol{v'_1}, \boldsymbol{v'_2},\dots, \boldsymbol{v'_n}\} を取りましょう。このとき, \{\boldsymbol{v'_k}\} は \{\boldsymbol{v_k}\} を用いて
\begin{aligned}\boldsymbol{v'_1} &= p_{11} \boldsymbol{ v_1}+p_{21} \boldsymbol{ v_2}+\cdots +p_{n1} \boldsymbol{ v_n} ,\\ \boldsymbol{ v'_2} &= p_{12} \boldsymbol{ v_1}+p_{22} \boldsymbol{ v_2} +\cdots + p_{n2} \boldsymbol{ v_n}, \\ &\ldots \\ \boldsymbol{ v'_n} &= p_{1n} \boldsymbol{ v_1}+p_{2n} \boldsymbol{ v_2} +\cdots + p_{nn} \boldsymbol{ v_n} \end{aligned}
とかけます。これは,行列を用いると,
とかけます。このときの,n 次正方行列 P=(p_{ij}) を基底の変換行列といいます。定義をまとめましょう。
定義(基底の変換行列)
V をベクトル空間とし, \{ \boldsymbol{v_1}, \boldsymbol{v_2},\dots, \boldsymbol{v_n}\} と \{ \boldsymbol{v'_1}, \boldsymbol{v'_2},\dots, \boldsymbol{v'_n}\} をどちらも基底とする。
\color{red} (\boldsymbol{v'_1}, \boldsymbol{v'_2}, \dots, \boldsymbol{v'_n}) = (\boldsymbol{v_1}, \boldsymbol{v_2}, \dots, \boldsymbol{v_n}) P
とかけるとき,このときの n 次正方行列 P を \{\boldsymbol{v_k}\} から \{\boldsymbol{v'_k}\} への基底の変換行列という。
ここで, P は必ず正則行列になります。すなわち, P には逆行列が存在します。
なぜならば「逆の基底の変換」も考えられることができますから,そのときの基底の変換行列を Q としたときに,\{ \boldsymbol{v_k}\} \to \{\boldsymbol{v'_k}\} \to \{\boldsymbol{v_k}\} や \{ \boldsymbol{v'_k}\} \to \{\boldsymbol{v_k}\} \to \{\boldsymbol{v'_k}\} という2回変換を考えることで, PQ=QP = I (単位行列) とならねばならないからです(分からなければ飛ばしてください)。
ところで,定義が「線形写像の表現行列」のときと似ていると思ったかもしれません。ちょっと比較してみましょう。
V, W を m,n 次元ベクトル空間とし, その基底を \{\boldsymbol{v_1},\boldsymbol{v_2},\ldots, \boldsymbol{v_m}\}, \{\boldsymbol{w_1},\boldsymbol{w_2},\ldots, \boldsymbol{w_n}\} とする。
線形写像 f\colon V\to W に関して,これらの基底を用いて
とかけるとき,このときの n\times m 行列 A を f の表現行列(行列表示)という。
m=n, \; f を同型写像と思って \{f(\boldsymbol{v_k})\} も W の基底と思うと,線形写像の表現行列は,基底 \{\boldsymbol{w_k}\} を \{f(\boldsymbol{v_k})\} に変換すると考えた基底の変換行列になります。
ここで,「定義は似ているがなんとなく逆である」と思ったら鋭いです。実際,模式的に以下のようにかきます。
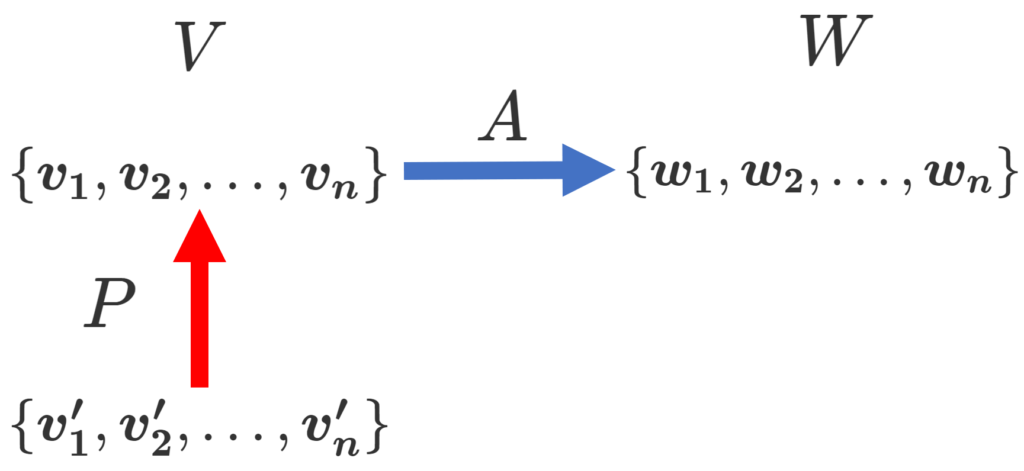
この際, \{ \boldsymbol{v_1}, \boldsymbol{v_2},\dots, \boldsymbol{v_n}\} と \{ f(\boldsymbol{v_1}), f(\boldsymbol{v_2}),\dots, f(\boldsymbol{v_n})\} を同一視しています。
写像の方は正しい方向に矢印が伸びているのに対し,基底の変換行列は逆向きに矢印が伸びているように感じるかもしません。分解して考えると以下のような感じです。

(f(\boldsymbol{v_1}) , f(\boldsymbol{v_2}) , \dots , f(\boldsymbol{v_m}) ) =( \boldsymbol{w_1} ,\boldsymbol{w_2} , \dots ,\boldsymbol{w_n} ) A と (\boldsymbol{v'_1}, \boldsymbol{v'_2}, \dots, \boldsymbol{v'_n}) = (\boldsymbol{v_1}, \boldsymbol{v_2}, \dots, \boldsymbol{v_n}) P でしたから,矢印の向きは統一されていることが確認できますね。
基底の変換行列の性質
さて,ここからは基底の変換行列の大事な性質である
- 基底の変換行列と成分表示
- 基底の変換行列と線形写像の表現行列
について,確認していきましょう。
基底の変換行列と成分表示
ある \boldsymbol{x}\in V が基底 \{\boldsymbol{v_k}\} を用いて,
\boldsymbol{x} = a_1\boldsymbol{v_1}+a_2\boldsymbol{v_2}+\cdots+ a_n\boldsymbol{v_n}
とかけているとしましょう。一方で,\{ \boldsymbol{v'_k}\} を用いて
とかき表せるとしましょう。すると,以下の定理が成立します。
定理(基底の変換行列と成分表示)
上の状況で,
\color{red}\begin{pmatrix}b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix}= P^{-1} \begin{pmatrix}a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix}
が成立する。
この定理を用いれば, a_1, a_2,\dots, a_n から b_1,b_2,\dots, b_n を求めることもできますね。
証明
\begin{aligned} &(\boldsymbol{v_1}, \dots, \boldsymbol{v_n})\begin{pmatrix} a_1 \\ \vdots \\ a_n \end{pmatrix} \\ &= \boldsymbol{x} =(\boldsymbol{v'_1}, \dots, \boldsymbol{v'_n})\begin{pmatrix} b_1 \\ \vdots \\ b_n\end{pmatrix} \\ &= (\boldsymbol{v_1}, \dots, \boldsymbol{v_n})P\begin{pmatrix} b_1 \\ \vdots \\ b_n\end{pmatrix} \end{aligned}
両辺を比較して,
両辺左から P^{-1} をかけると,
証明終
基底の変換行列と線形写像の表現行列
基底を変換すると,線形写像の表現行列は以下のように変化します。これは,非常に重要な定理です。
定理(基底の変換行列と線形写像の表現行列)
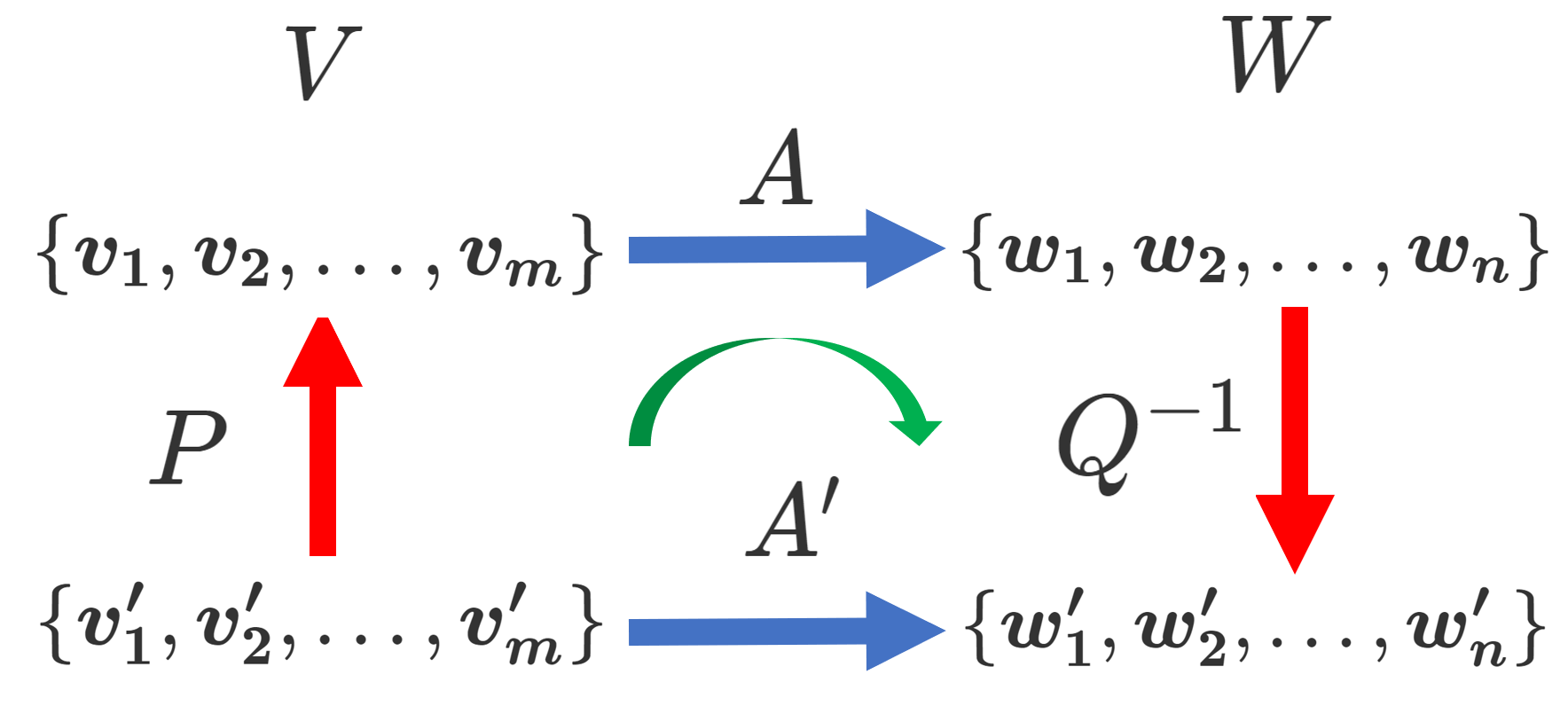
V, W をベクトル空間とし, \{ \boldsymbol{v_1}, \boldsymbol{v_2},\dots, \boldsymbol{v_m}\} と \{ \boldsymbol{w_1}, \boldsymbol{w_2},\dots, \boldsymbol{w_n}\} をそれぞれの基底とする。さらに,それとは別の基底を,基底の変換行列が
\begin{aligned} ( \boldsymbol{v'_1}, \boldsymbol{v'_2},\dots, \boldsymbol{v'_m}) &= ( \boldsymbol{v_1}, \boldsymbol{v_2},\dots, \boldsymbol{v_m}) P, \\ ( \boldsymbol{w'_1}, \boldsymbol{w'_2},\dots, \boldsymbol{w'_n}) &= ( \boldsymbol{w_1}, \boldsymbol{w_2},\dots, \boldsymbol{w_n}) Q\end{aligned}
となるようにとる。さらに,線形写像 f \colon V\to W に対し,
基底 \{ \boldsymbol{v_1}, \boldsymbol{v_2},\dots, \boldsymbol{v_m}\},\; \{ \boldsymbol{w_1}, \boldsymbol{w_2},\dots, \boldsymbol{w_n}\} に関する表現行列(行列表示)を A ,
基底 \{ \boldsymbol{v'_1}, \boldsymbol{v'_2},\dots, \boldsymbol{v'_m}\},\; \{ \boldsymbol{w'_1}, \boldsymbol{w'_2},\dots, \boldsymbol{w'_n}\} に関する表現行列(行列表示)を A' とする。
このとき,
である。
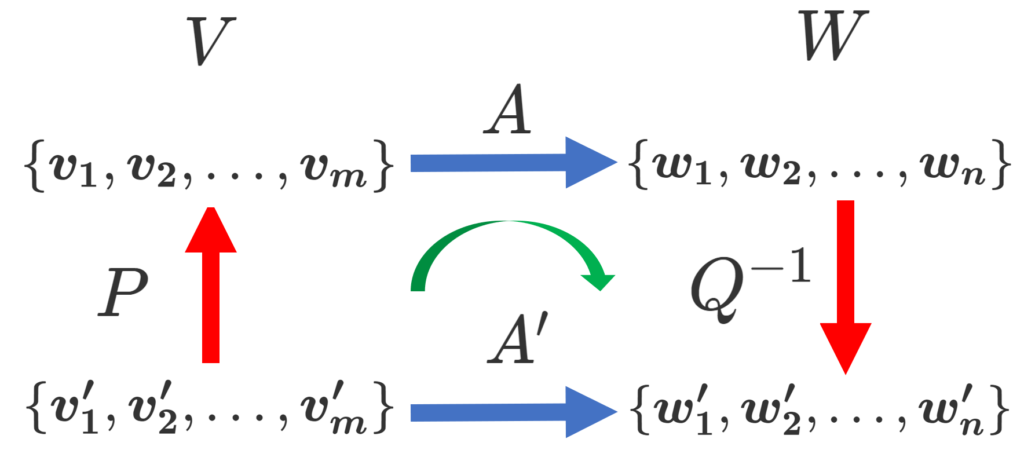
上の図において,行列の積は,線形写像の合成に対応しており,線形写像の合成と同様,右から計算されることに注意してください。
基底の変換に対して,線形写像の表現行列がどう変化するかを述べた定理です。線形写像をできるだけ簡便な表現行列で扱いたいと思ったとき,基底の変換は必須です。証明しましょう。
証明
(f(\boldsymbol{v_1}) , \dots , f(\boldsymbol{v_m}) ) を簡単のため, f(\boldsymbol{v_1},\dots, \boldsymbol{v_n}) とかくことにする。
f の線形性より,
\begin{aligned} f( \boldsymbol{v'_1},\dots, \boldsymbol{v'_m}) &= f( ( \boldsymbol{v_1}, \dots, \boldsymbol{v_m}) P) \\ & = f ( \boldsymbol{v_1},\dots, \boldsymbol{v_m}) P \\ &= ( \boldsymbol{w_1},\dots, \boldsymbol{w_n}) AP . \end{aligned}
また, ( \boldsymbol{w'_1},\dots, \boldsymbol{w'_n}) = ( \boldsymbol{w_1},\dots, \boldsymbol{w_n}) Q の右から Q^{-1} をかけることで, ( \boldsymbol{w'_1},\dots, \boldsymbol{w'_n}) Q^{-1}= ( \boldsymbol{w_1},\dots, \boldsymbol{w_n}) であるから,これを用いると,
よって, A' = Q^{-1} AP.
証明終
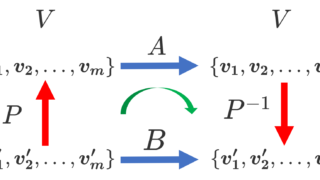
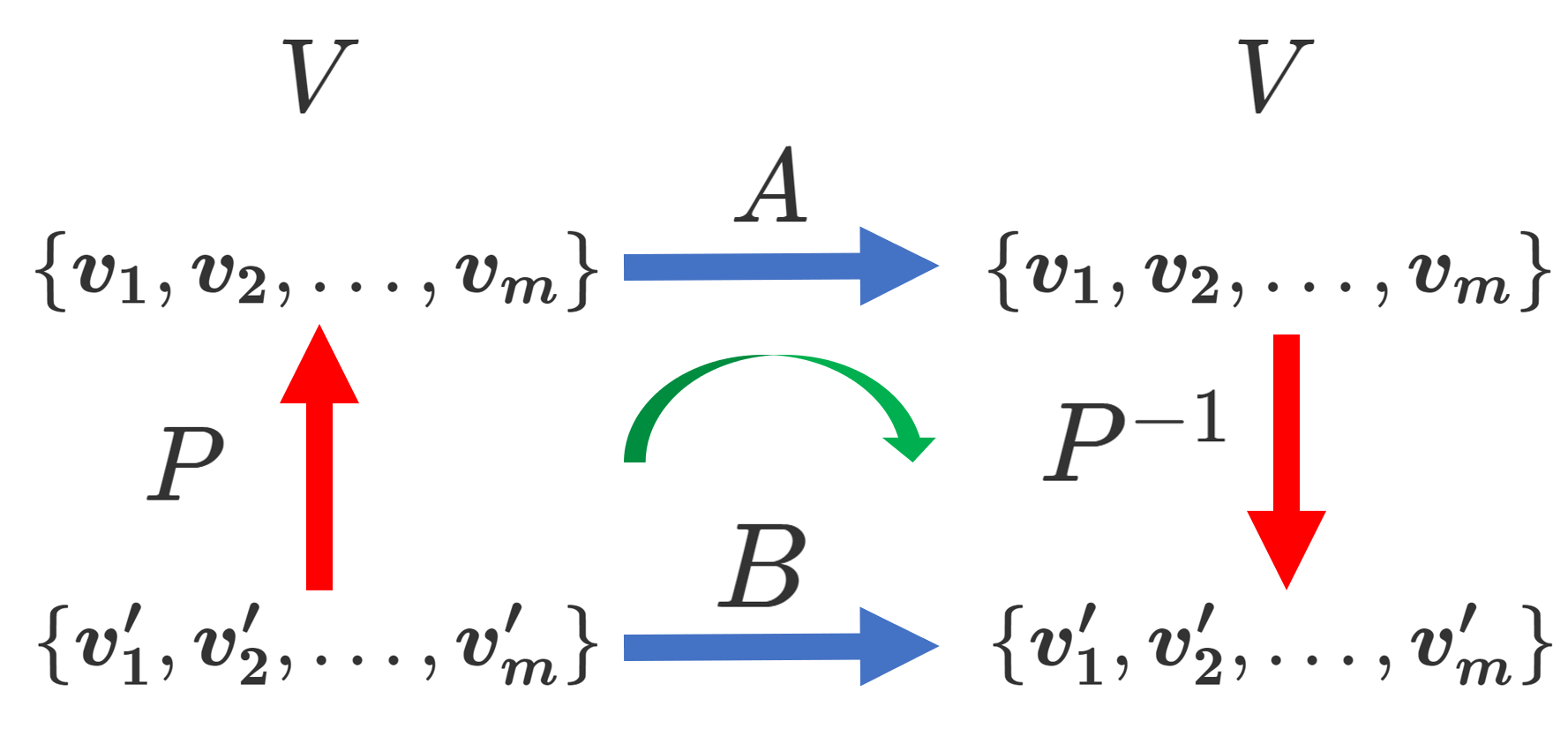
行列の相似
上において, f\colon V\to V とし,基底 \{ \boldsymbol{v_1}, \boldsymbol{v_2},\dots, \boldsymbol{v_m}\} による表現行列を A,基底 \{ \boldsymbol{v'_1}, \boldsymbol{v'_2},\dots, \boldsymbol{v'_m}\} による表現行列を A' とすると,
A' = P^{-1}AP
となります。このとき,行列 A, A' は相似 (similar) であるといいます。
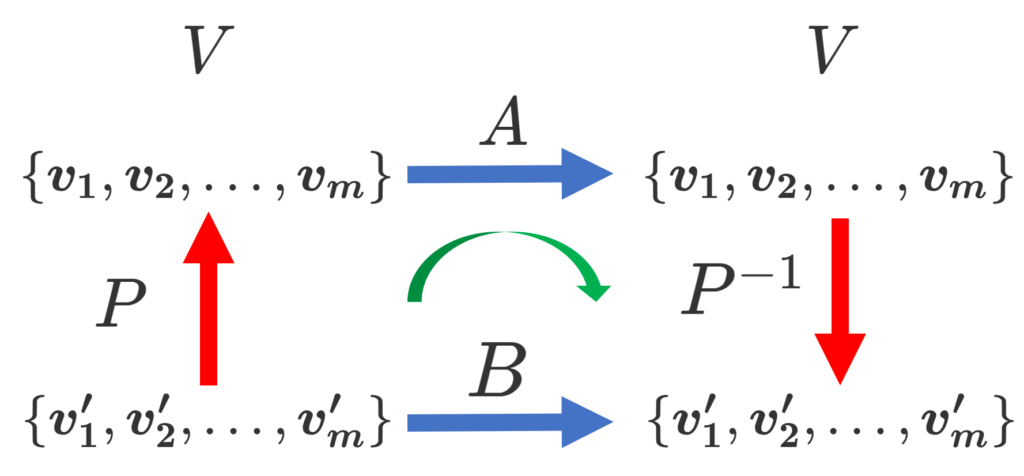
これについては,さまざまな良い性質がありますから,別途,以下で解説しています。