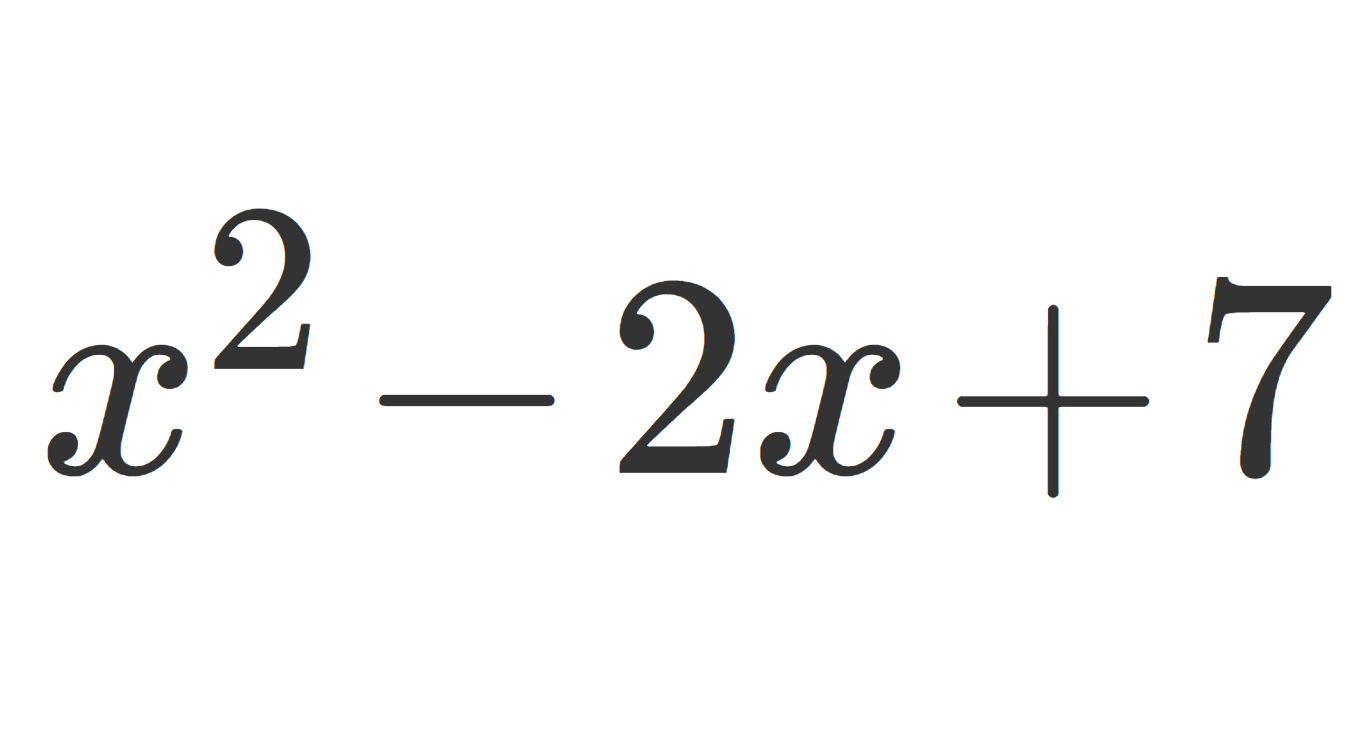モニック多項式とは～定義・例・性質～

モニック多項式とは，最高次係数が $1$ である一変数多項式のことを言います。モニック多項式について，簡単に定義・例・性質を紹介しましょう。

モニック多項式とは

定義（モニック多項式）

最高次係数が $1$ である一変数多項式をモニック多項式 (monic polynomial) という。すなわち，

\color{red}p(x)=x^n+c_{n-1}x^{n-1}+c_{n-2}x^{n-2}+\dots +c_0

のような多項式のことをモニック多項式という。

より一般に，可換環 $R$ 上の一変数多項式環

R[x]=\left\{ \sum_{k=0}^n r_k x^k\middle|n\ge 0,\, r_0,\dots, r_n \in R\right\}

について，最高次係数が $1\in R$ (乗法単位元)になる多項式もモニック多項式 (monic polynomial) といいます。

普通に「最高次係数が $1$ の多項式って言えばいいじゃん」って思うかもしれませんが，名前を付けるくらい，代数学では考える価値のある多項式です。

一応例を挙げておきましょう。

モニック多項式の例

モニック多項式でない例

モニック多項式の簡単な性質を紹介しましょう。

定理1（モニック多項式の積もモニック）

$f, g$ がモニック多項式なら，その積 $fg$ もモニック多項式である。特に，モニック多項式全体の集合は乗法に関してモノイド(単位元を持つ半群)になる。

単に，最高次係数が $1$ の多項式をかけ算してもやはり最高次係数が $1$ になる，と言っているに過ぎません。

定理2（多項式の割り算）

$R$ を可換環， $R[x]$ を $R$ 係数の多項式環とする。 $g\in R[x]$ をモニックとするとき，任意の $f\in R[x]$ は

\color{red}\begin{gathered}f=gq+r , \quad q, r\in R[x]\\ \deg r< \deg g \end{gathered}

とかける。ただし， $\deg f$ は $f$ の次数を表す。これを多項式の割り算という。

体上の多項式環であれば， $g$ はモニックでなくても「多項式の割り算」ができますが，環上の多項式環について「多項式の割り算」を定義するには，モニック多項式で割らねばなりません。

難しく聞こえるかもしれませんが，要するに「整数係数の多項式を最高次係数が $1$ の整数係数多項式で割り算すると，商も余りも整数係数になるが，最高次係数が $1$ でない多項式で割り算すると，商・余りが整数係数になるとは限らない」というのを難しく言っていると考えても大丈夫です。