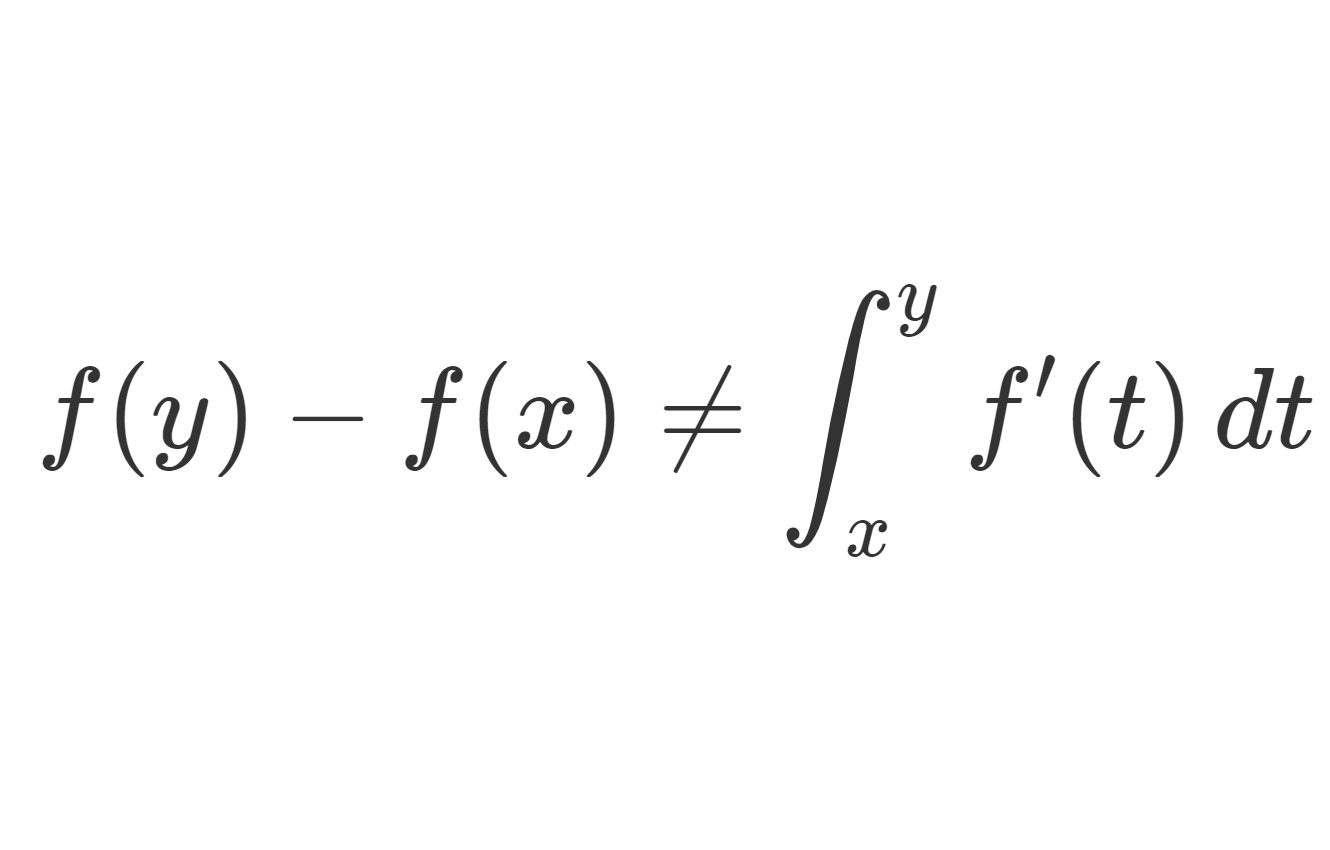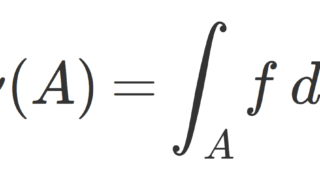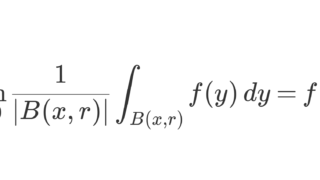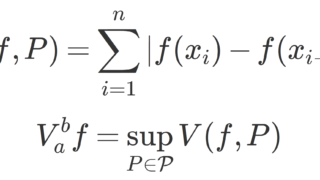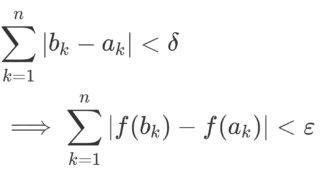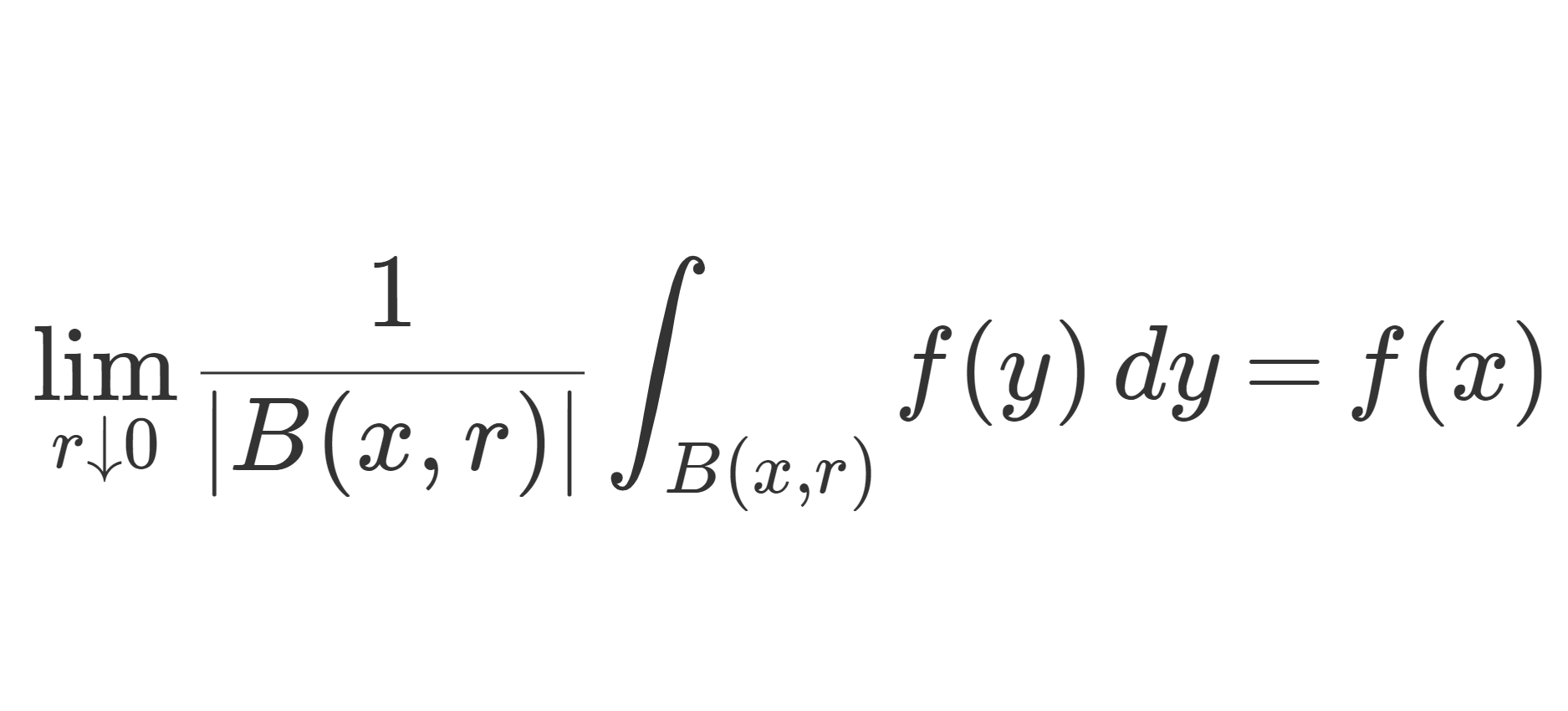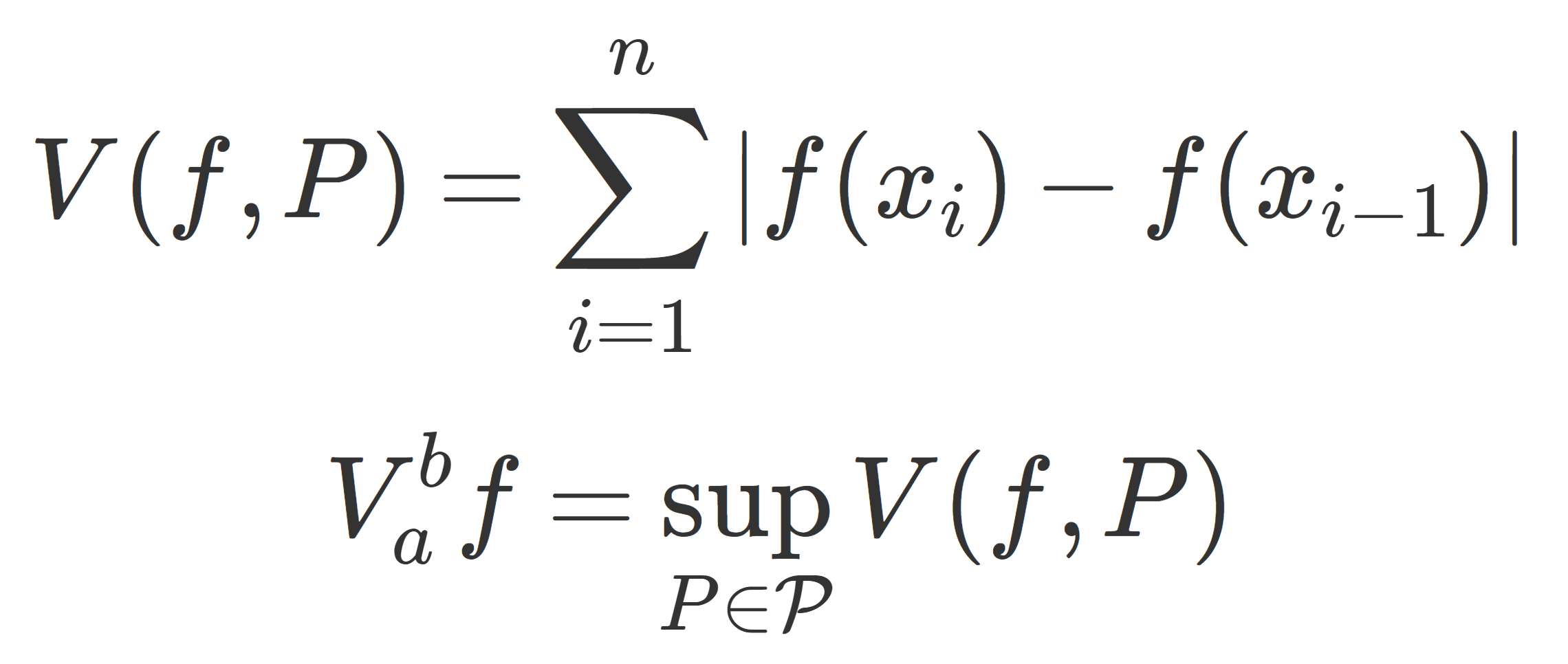単調増加または単調減少関数,より一般に有界変動関数は,ほとんどいたるところ微分可能であることが知られています。
これについて,ラドンニコディムの定理やルベーグの微分定理を用いた証明を紹介しましょう。
単調関数はほとんどいたるところ微分可能
定理1(単調関数におけるルベーグの定理)
f\colon [a,b]\to \R は広義単調増加とする。このとき, f はほとんどいたるところ微分可能である。
単調関数でなくとも,2つの単調増加関数 f_1,f_2 の差でかける関数 f(x)=f_1(x)-f_2(x) も,ほとんどいたるところ微分可能です。このようにかける関数 f を有界変動関数 (bounded variation function) といいます(→有界変動関数の定義と例といくつかの大事な性質)。
そもそも単調関数は連続なのか,と思ったかもしれません。単調関数は連続ではありませんが,高々可算個の点を除いて連続であることが知られています。これの証明は,以下で行っています。
証明には,以下の知識を用いることにします。
証明
f は広義単調増加であるから, \widetilde{f}(x)=\lim_{y \uparrow x}f(y) は存在して,\widetilde{f} は左連続である。ゆえに,
\nu([a,x))=\widetilde{f}(x)-\widetilde{f}(a)
によって測度 \nu が定まる。測度に関するルベーグ分解より,
であって, \nu_c はルベーグ測度 m に関して絶対連続( \nu_c\ll m)であり, \nu_s はルベーグ測度 m に関して特異( \nu_s\perp m)であるものが存在する。
g=d\nu_c/dm をラドンニコディム微分とすると,ルベーグの微分定理における測度の微分の項目より,
\begin{aligned} &\frac{\nu([x, x+h))}{m([x, x+h))} \\ & =\frac{\nu_c([x, x+h))}{m([x, x+h))}+\frac{\nu_s([x, x+h))}{m([x, x+h))} \\ &\xrightarrow{h\downarrow 0} g(x)+0,\quad m\text{-a.e.} \end{aligned}
が成り立つ。 m([x,x+h))=h と \nu の定義より,
となる。Frodaの定理より,不連続点は高々可算個であるから, f(x)=\widetilde{f}(x),\, m\text{-a.e. }\, x \in [a,b] である。このような x \in [a,b] について,
である。ここで, \delta >1 とする。 f は広義単調増加なので, h>0 に対し, \widetilde{f}(x+h)\le f(x+h)\le \widetilde{f}(x+\delta h) である。したがって,
すなわち,
である。 \delta\downarrow 1 とすることで,
がわかる。全く同様に,
も証明できるため,証明が終わる。
証明終
証明中の g は f' と書かれるのが普通です。ここで注意ですが,一般に
f(y)-f(x)=\int_x^y f'(t)\, dt,\quad a\le x<y<\le b
は成立しません。たとえば, f(x)=\begin{cases}x^2\sin (1/x^2) & x\ne 0, \\ 0 & x=0 \end{cases} について, f は任意の点で微分可能ですが, \int_0^1 |f'(t)|\, dt=\infty となってしまいます。
他にも, f をカントール関数とすると, f(0)=0,\, f(1)=1 で広義単調増加のため, [0,1] 上ほとんどいたるところ微分可能ですが, f'(x)=0,\, \text{a.e.} となり,
f(1)-f(0) \ne \int_0^1 f'(t)\, dt
となっています。また,より簡単に f(x)=\begin{cases} 0 & 0\le x\le 1/2,\\ 1& 1/2<x\le 1\end{cases} でも f'(x)=0,\, \text{a.e.} となって同様です。
絶対連続関数の微分
さて,一般には
f(y)-f(x)\ne \int_x^y f'(t)\, dt
であると述べました。 f が絶対連続関数と呼ばれる関数のとき,等号が成立することが知られています。まずは,絶対連続関数が何か述べましょう。
f\colon [a,b]\to \R が絶対連続関数 (absolutely continuous function) であるとは,任意の \varepsilon >0 に対して,ある \delta>0 が存在して,任意の n \ge 1 と任意の互いに素な区間列 \{ (x_k, y_k)\}_{k=1}^n に対し,
\sum_{k=1}^n|y_k-x_k|<\delta \implies \sum_{k=1}^n|f(y_k)-f(x_k)|<\varepsilon
が成り立つことを言う。
f が絶対連続関数であり, E\subset \R が零集合であるとき,像 f(E) も零集合になることが知られている。
詳しくは絶対連続な関数とは~定義と例と性質4つ~で解説しています。
絶対連続関数は有界変動関数の一種であり,ほとんどいたるところ微分可能です。さらに一般には成り立たない
f(y)-f(x)=\int_x^y f'(t)\, dt
が成立します。
定理2
f\colon [a,b]\to \R を絶対連続関数とする。このとき, f はほとんどいたるところ微分可能であり,その微分を f' とすると,
\color{red}f(y)-f(x)=\int_x^y f'(t)\, dt,\quad a\le x<y\le b
が成立する。
証明しましょう。
証明
f は広義単調増加であるとして示せばよい。 f は絶対連続なので連続である。
\nu([a,x))=f(x)-f(a)
によって測度 \nu が定まる。 f は零集合を零集合に移すから, \nu はルベーグ測度 m と絶対連続( \nu\ll m)である。
f'=d\nu/dm をラドンニコディム微分とすると,定理1の証明と同様に,
\lim_{h\to 0}\frac{f(x+h)-{f}(x)}{h} =f'(x), \quad m\text{-a.e. }
である。また,ラドンニコディム微分の定義より, a\le x<y\le b に対し,
すなわち,
証明終